Chapter 11 Bayesian Models of Cognition

11.0.1 Introduction

The impressive power of Bayes theorem and Bayesian approaches to modeling has tempted cognitive scientists into exploring how far they could get in thinking the mind and brain as Bayesian machines. The idea is that the mind is a probabilistic machine that updates its beliefs based on the evidence it receives. The human mind constantly receives input from various sources – direct personal experience, social information from others, prior knowledge, and sensory input. A fundamental question in cognitive science is how these disparate pieces of information are combined to produce coherent beliefs about the world. The Bayesian framework offers a powerful approach to modeling this process. Under this framework, the mind is conceptualized as a probabilistic machine that continuously updates its beliefs based on new evidence. This contrasts with rule-based or purely associative models by emphasizing:

Representations of uncertainty: Beliefs are represented as probability distributions, not single values
Optimal integration: Information is combined according to its reliability
Prior knowledge: New evidence is interpreted in light of existing beliefs

In this chapter, we will explore how Bayesian integration can be formalized and used to model cognitive processes. We’ll start with simple models that give equal weight to different information sources, then develop more sophisticated models that allow for differential weighting based on source reliability, and finally consider how beliefs might update over time.

This chapter is not a comprehensive review of Bayesian cognitive modeling, but rather a practical introduction to the topic. We’ll focus on simple models that illustrate key concepts and provide a foundation for more advanced applications.

To go further in your learning check on Bayesian models of cognition check:

Ma, W. J., Kording, K. P., & Goldreich, D. (2023). Bayesian models of perception and action: An introduction. MIT press.
Griffiths, T. L., Chater, N., & Tenenbaum, J. B. (Eds.). (2024). Bayesian models of cognition: reverse engineering the mind. MIT Press.
N. D. Goodman, J. B. Tenenbaum, and The ProbMods Contributors (2016). Probabilistic Models of Cognition (2nd ed.). Retrieved 2025-3-10 from https://probmods.org/

11.1 Learning Objectives

After completing this chapter, you will be able to:

Understand the basic principles of Bayesian information integration
Implement models that combine multiple sources of information in a principled Bayesian way
Fit and evaluate these models using Stan
Differentiate between alternative Bayesian updating schemes
Apply Bayesian cognitive models to decision-making data

11.2 Chapter Roadmap

In this chapter, we will:

Introduce the Bayesian framework for cognitive modeling
Implement a simple Bayesian integration model
Develop and test a weighted Bayesian model that allows for different source reliability
Explore temporal Bayesian updating
Extend our models to multilevel structures that capture individual differences
Compare alternative Bayesian models and evaluate their cognitive implications

11.3 The Bayesian Framework for Cognition

Bayesian models of cognition explore the idea that the mind operates according to principles similar to Bayes’ theorem, combining different sources of evidence to form updated beliefs. Most commonly this is framed in terms of prior beliefs being updated with new evidence to form updated posterior beliefs. Formally:

P(belief | evidence) ∝ P(evidence | belief) × P(belief)

Where:

P(belief | evidence) is the posterior belief after observing evidence
P(evidence | belief) is the likelihood of observing the evidence given a belief
P(belief) is the prior belief before observing evidence

In cognitive terms, this means people integrate new information with existing knowledge, giving more weight to reliable information sources and less weight to unreliable ones. Yet, there is nothing mathematically special about the prior and the likelihood. They are just two sources of information that are combined in a way that is consistent with the rules of probability. Any other combination of information sources can be modeled with the same theorem.

Note that a more traditional formula for Bayes Theorem would be

P(belief | evidence) = [P(evidence | belief) × P(belief)] / P(evidence)

where the product of prior and likelihood is normalized by P(evidence) (bringing it back to a probability scale). That’s why we used a ∝ symbol in the formula above, to indicate that we are not considering the normalization constant, and that the posterior is only proportional (and not exactly equal) to the multiplication of the two sources of information. Nevertheless, this is a first useful approximation of the theorem, which we can build on in the rest of the chapter. ***

11.4 Visualizing Bayesian Updating

To better understand Bayesian updating, let’s create a conceptual diagram:

# Create a visualization of Bayesian updating process

# Function to create Bayesian updating visualization
create_bayesian_updating_diagram <- function() {
  # Create example data
  # Prior (starting with uniform distribution)
  x <- seq(0, 1, by = 0.01)
  prior <- dbeta(x, 1, 1)
  
  # Likelihood (evidence suggesting higher probability)
  likelihood <- dbeta(x, 7, 3)
  
  # Posterior (combines prior and likelihood)
  posterior <- dbeta(x, 8, 4)  # 1+7, 1+3
  
  # Create data frame for plotting
  plot_data <- data.frame(
    x = rep(x, 3),
    density = c(prior, likelihood, posterior),
    distribution = factor(rep(c("Prior", "Likelihood", "Posterior"), each = length(x)),
                         levels = c("Prior", "Likelihood", "Posterior"))
  )
  
  # Create main plot showing distributions
  p1 <- ggplot(plot_data, aes(x = x, y = density, color = distribution, linetype = distribution)) +
    geom_line(size = 1.2) +
    scale_color_manual(values = c("Prior" = "blue", "Likelihood" = "red", "Posterior" = "purple")) +
    scale_linetype_manual(values = c("Prior" = "dashed", "Likelihood" = "dotted", "Posterior" = "solid")) +
    labs(title = "Bayesian Updating Process",
         subtitle = "Combining prior beliefs with new evidence",
         x = "Belief (probability)",
         y = "Probability Density",
         color = "Distribution",
         linetype = "Distribution") +
    theme_minimal() +
    theme(legend.position = "bottom") +
    annotate("text", x = 0.1, y = 0.9, label = "Low certainty\nprior belief", color = "blue", hjust = 0) +
    annotate("text", x = 0.8, y = 1.5, label = "New evidence\nsuggests high\nprobability", color = "red", hjust = 1) +
    annotate("text", x = 0.65, y = 2.2, label = "Updated belief\ncombines both\nsources", color = "purple", hjust = 0)
  
  # Create flow diagram to illustrate process
  flow_data <- data.frame(
    x = c(1, 2, 3),
    y = c(1, 1, 1),
    label = c("Prior\nBelief", "Evidence", "Posterior\nBelief"),
    box_color = c("blue", "red", "purple")
  )
  
  arrow_data <- data.frame(
    x = c(1.3, 2.3),
    xend = c(1.7, 2.7),
    y = c(1, 1),
    yend = c(1, 1)
  )
  
  p2 <- ggplot() +
    # Add boxes for process stages
    geom_rect(data = flow_data, aes(xmin = x - 0.3, xmax = x + 0.3, 
                                   ymin = y - 0.3, ymax = y + 0.3,
                                   fill = box_color), color = "black", alpha = 0.3) +
    # Add text labels
    geom_text(data = flow_data, aes(x = x, y = y, label = label), size = 3.5) +
    # Add arrows
    geom_segment(data = arrow_data, aes(x = x, y = y, xend = xend, yend = yend),
                arrow = arrow(length = unit(0.2, "cm"), type = "closed")) +
    # Add the operation being performed
    annotate("text", x = 1.5, y = 1.2, label = "×", size = 6) +
    annotate("text", x = 2.5, y = 1.2, label = "∝", size = 5) +
    # Formatting
    scale_fill_manual(values = c("blue", "red", "purple")) +
    theme_void() +
    theme(legend.position = "none") +
    labs(title = "Bayesian Inference Flow")
  
  # Combine plots vertically
  combined_plot <- p1 / p2 + plot_layout(heights = c(4, 1))
  
  return(combined_plot)
}

# Generate and display the diagram
create_bayesian_updating_diagram()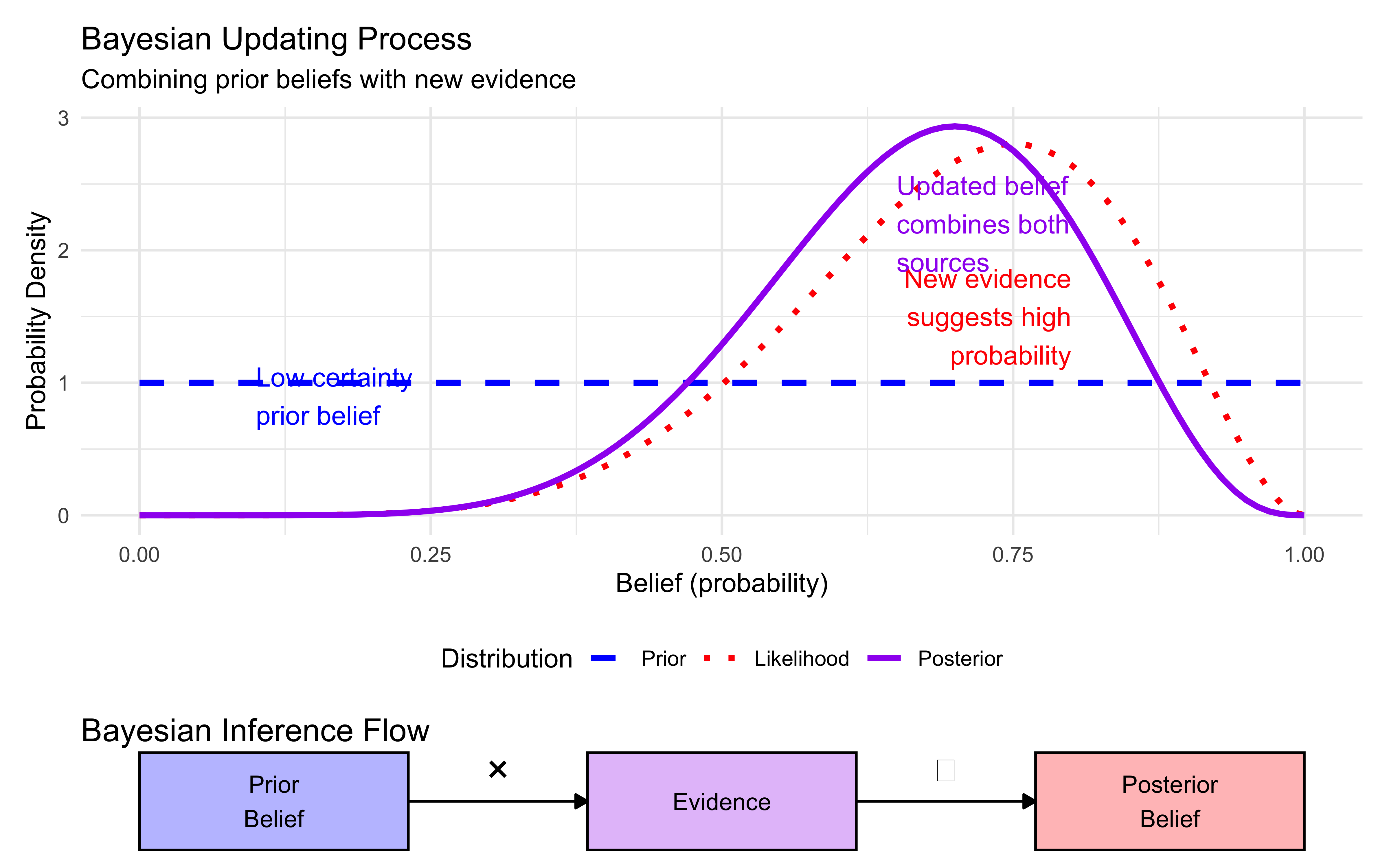

This diagram illustrates the key elements of Bayesian updating:

Prior belief (blue dashed line): Our initial uncertainty about a phenomenon, before seeing evidence
Likelihood (red dotted line): The pattern of evidence we observe
Posterior belief (purple solid line): Our updated belief after combining prior and evidence

Notice how the posterior distribution:

Is narrower than either the prior or likelihood alone (indicating increased certainty)
Sits between the prior and likelihood, but closer to the likelihood (as the evidence was fairly strong)
Has its peak shifted from the prior toward the likelihood (reflecting belief updating)

The bottom diagram shows the algebraic process: we multiply the prior by the likelihood, then normalize to get the posterior belief.

11.5 Bayesian Models in Cognitive Science

Bayesian cognitive models have been successfully applied to a wide range of phenomena:

Perception: How we combine multiple sensory cues (visual, auditory, tactile) to form a unified percept
Learning: How we update our knowledge from observation and instruction
Decision-making: How we weigh different sources of evidence when making choices
Social cognition: How we integrate others’ opinions with our own knowledge
Language: How we disambiguate words and sentences based on context
Psychopathology: How crucial aspects of conditions like schizophrenia and autism can be understood in terms of atypical Bayesian inference (e.g. atypical weights given to different sources of information, or hyper-precise priors or hyper-precise likelihood).

11.7 A Bayesian Integration Model for the Marble Task

In a fully Bayesian approach, participants would:

Use direct evidence to form a belief about the proportion of blue marbles in the jar
Use social evidence to form another belief about the same proportion
Combine these beliefs in a principled way to make their final judgment

11.7.1 Intuitive Explanation Using Beta Distributions

The beta distribution provides an elegant way to represent beliefs about proportions (like the proportion of blue marbles in a jar):

The beta distribution is defined by two parameters, traditionally called α (alpha) and β (beta).
These parameters have an intuitive interpretation: you can think of α as the number of “successes” you’ve observed (e.g., blue marbles) plus 1, and β as the number of “failures” (e.g., red marbles) plus 1.
So a Beta(1,1) distribution represents a uniform belief - no prior knowledge about the proportion.
After observing evidence, you simply add the counts to these parameters:
- If you see 6 blue and 2 red marbles, your updated belief is Beta(1+6, 1+2) = Beta(7, 3)
- This distribution has its peak at 7/(7+3) = 0.7, reflecting your belief that the true proportion is around 70% blue
To combine multiple sources of evidence, you simply add all the counts together:
- If direct evidence gives Beta(7, 3) and social evidence suggests Beta(2, 4)
- Your combined belief is Beta(7+2, 3+4) = Beta(9, 7)
- This has its peak at 9/(9+7) = 0.56, reflecting a compromise between the two sources

The beauty of this approach is that it automatically weights evidence by its strength (amount of data) and properly represents uncertainty through the width of the distribution.

11.8 The Mathematical Model

For our marble task, the Bayesian inference process involves:

11.8.1 Evidence Representation

Direct evidence: Observing blue1 blue marbles and red1 red marbles out of total1 trials
Social evidence: Inferring blue2 blue marbles and red2 red marbles from social information. If we consider only their choice: red corresponds to the sampling of one red marble; blue corresponds to the sampling of one blue marble. If we consider their confidence, we might try to make this correspond to the marbles the sampled: “Clear blue” might imply 8 blue marbles; maybe blue might imply 6 blue and 2 red marbles; “maybe red” might imply 6 red and 2 blue marbles; “clear red” might imply 8 red marbles. Alternatively we can keep it more uncertain and reduce the assumed sample to 0 blue out of 3, 1 blue out of 3, 2 blue marbles out of 3, or 3 blue marbles out of 3. This intrinsically models the added uncertainty in observing the other’s choice and not their samples.

11.8.2 Integration

The integrated belief is represented by a posterior beta distribution:

Beta(α + blue1 + blue2, β + red1 + red2)

Where α and β are prior parameters (typically 1 each for a uniform prior)

11.8.3 Decision

Final choice (blue or red) depends on whether the expected value of this distribution is above 0.5
Confidence depends on the concentration of the distribution

11.8.4 Implementation in R

# Beta-binomial model for Bayesian integration in the marble task
#
# This function implements a Bayesian integration model for combining direct and social evidence
# about the proportion of blue marbles in a jar. It uses the beta-binomial model, which is
# particularly suitable for reasoning about proportions.
#
# Parameters:
#   alpha_prior: Prior alpha parameter (conceptually: prior blue marbles + 1)
#   beta_prior: Prior beta parameter (conceptually: prior red marbles + 1)
#   blue1: Number of blue marbles in direct evidence
#   total1: Total marbles in direct evidence
#   blue2: Effective blue marbles from social evidence
#   total2: Effective total marbles from social evidence
#
# Returns:
#   List with posterior parameters and statistics for decision-making
betaBinomialModel <- function(alpha_prior, beta_prior, blue1, total1, blue2, total2) {
  # Calculate red marbles for each source
  red1 <- total1 - blue1  # Number of red marbles in direct evidence
  red2 <- total2 - blue2  # Inferred number of red marbles from social evidence
  
  # The key insight of Bayesian integration: simply add up all evidence counts
  # This automatically gives more weight to sources with more data
  alpha_post <- alpha_prior + blue1 + blue2  # Posterior alpha (total blues + prior)
  beta_post <- beta_prior + red1 + red2      # Posterior beta (total reds + prior)
  
  # Calculate posterior statistics
  expected_rate <- alpha_post / (alpha_post + beta_post)  # Mean of beta distribution
  
  # Variance has a simple formula for beta distributions
  # Lower variance = higher confidence in our estimate
  variance <- (alpha_post * beta_post) / 
             ((alpha_post + beta_post)^2 * (alpha_post + beta_post + 1))
  
  # Calculate 95% credible interval using beta quantile functions
  # This gives us bounds within which we believe the true proportion lies
  ci_lower <- qbeta(0.025, alpha_post, beta_post)
  ci_upper <- qbeta(0.975, alpha_post, beta_post)
  
  # Calculate confidence based on variance
  # Higher variance = lower confidence; transform to 0-1 scale
  confidence <- 1 - (2 * sqrt(variance))
  confidence <- max(0, min(1, confidence))  # Bound between 0 and 1
  
  # Make decision based on whether expected rate exceeds 0.5
  # If P(blue) > 0.5, choose blue; otherwise choose red
  choice <- ifelse(expected_rate > 0.5, "Blue", "Red")
  
  # Return all calculated parameters in a structured list
  return(list(
    alpha_post = alpha_post,
    beta_post = beta_post,
    expected_rate = expected_rate,
    variance = variance,
    ci_lower = ci_lower,
    ci_upper = ci_upper,
    confidence = confidence,
    choice = choice
  ))
}

11.8.5 Simulating Experimental Scenarios

We’ll create a comprehensive set of scenarios by varying both direct evidence (number of blue marbles observed directly) and social evidence (number of blue marbles inferred from social information).

# Set total counts for direct and social evidence
total1 <- 8  # Total marbles in direct evidence
total2 <- 3  # Total evidence units in social evidence

# Create all possible combinations of direct and social evidence
scenarios <- expand_grid(
  blue1 = seq(0, 8, 1),  # Direct evidence: 0 to 8 blue marbles
  blue2 = seq(0, 3, 1)   # Social evidence: 0 to 3 blue marbles (confidence levels)
) %>% mutate(
  red1 = total1 - blue1,  # Calculate red marbles for direct evidence
  red2 = total2 - blue2   # Calculate implied red marbles for social evidence
)

# Process all scenarios to generate summary statistics
sim_data <- map_dfr(1:nrow(scenarios), function(i) {
  # Extract scenario parameters
  blue1 <- scenarios$blue1[i]
  red1 <- scenarios$red1[i]
  blue2 <- scenarios$blue2[i]
  red2 <- scenarios$red2[i]
  
  # Calculate Bayesian integration using our model
  result <- betaBinomialModel(1, 1, blue1, total1, blue2, total2)
  
  # Return summary data for this scenario
  tibble(
    blue1 = blue1,
    red1 = red1,
    blue2 = blue2,
    red2 = red2,
    expected_rate = result$expected_rate,
    variance = result$variance,
    ci_lower = result$ci_lower,
    ci_upper = result$ci_upper,
    choice = result$choice,
    confidence = result$confidence
  )
})

# Convert social evidence to meaningful labels for better visualization
sim_data$social_evidence <- factor(sim_data$blue2,
                                 levels = c(0, 1, 2, 3),
                                 labels = c("Clear Red", "Maybe Red", "Maybe Blue", "Clear Blue"))

11.8.6 Visualizing Bayesian Integration

Let’s examine how expected proportion and uncertainty vary across different evidence combinations:

# Create two plot panels to visualize model behavior across all evidence combinations
p1 <- ggplot(sim_data, aes(x = blue1, y = expected_rate, color = social_evidence, group = social_evidence)) +
  # Add credible intervals to show uncertainty
  geom_ribbon(aes(ymin = ci_lower, ymax = ci_upper, fill = social_evidence), alpha = 0.2, color = NA) +
  geom_line(size = 1) +
  geom_point(size = 3) +
  geom_hline(yintercept = 0.5, linetype = "dashed", color = "gray50") +
  scale_x_continuous(breaks = 0:8) +
  scale_color_brewer(palette = "Set1") +
  scale_fill_brewer(palette = "Set1") +
  labs(title = "Bayesian Integration of Direct and Social Evidence",
       subtitle = "Expected proportion with 95% credible intervals",
       x = "Number of Blue Marbles in Direct Sample (out of 8)",
       y = "Expected Proportion of Blue Marbles",
       color = "Social Evidence",
       fill = "Social Evidence") +
  theme_bw() +
  coord_cartesian(ylim = c(0, 1))

# Display plot
p1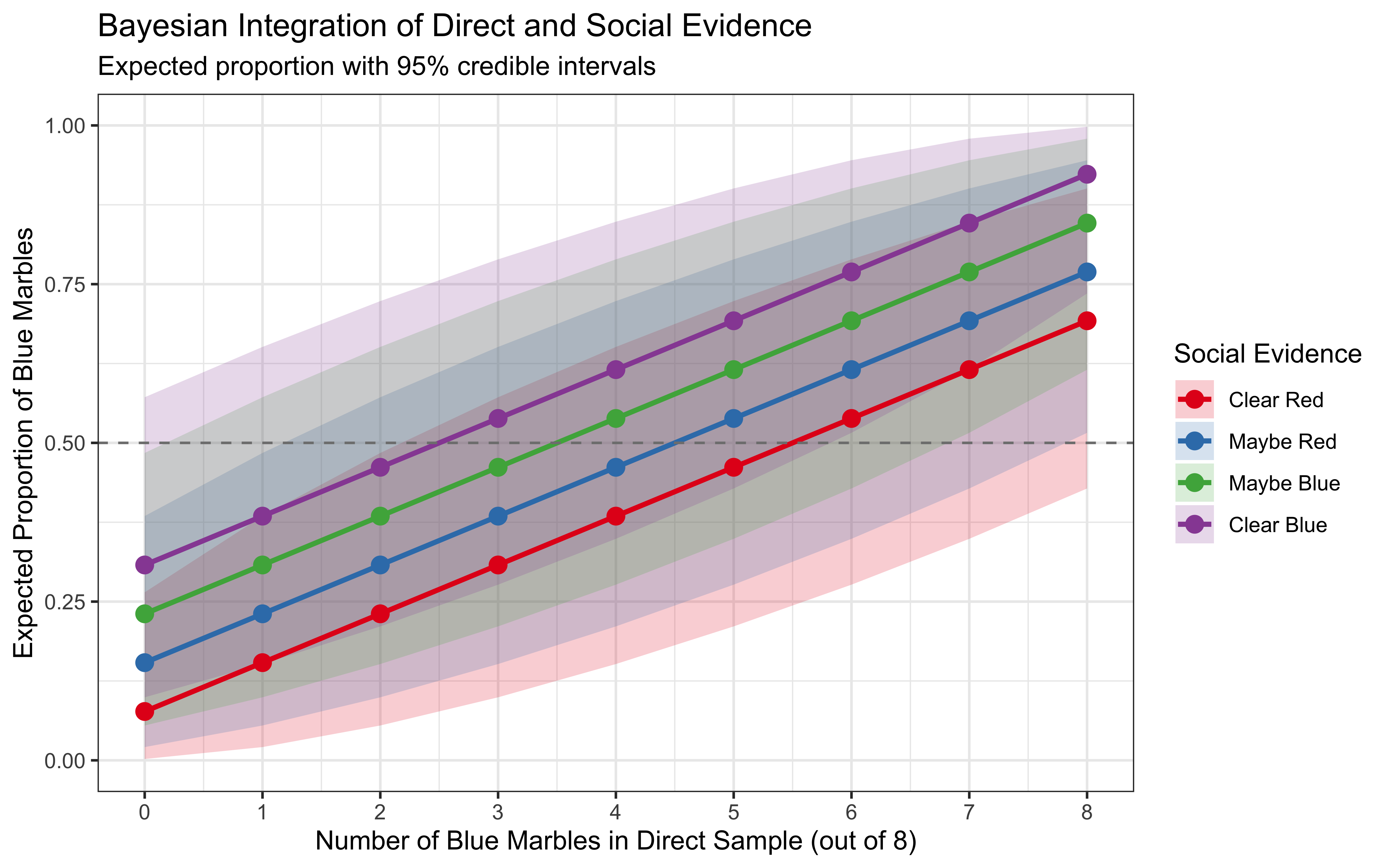

A few notes about the plot:

Evidence integration: The expected proportion of blue marbles (top plot) varies with both direct and social evidence. I would normally expect a non-linear interaction: when direct evidence is ambiguous (e.g., 4 blue out of 8), social evidence should have a stronger effect on the final belief. However, the effect is subtle if any.
Evidence Interaction: It may be hard to see, but the influence of social evidence is strongest when direct evidence is ambiguous (around 4 blue marbles) and weakest at the extremes (0 or 8 blue marbles). This reflects the Bayesian property that stronger evidence dominates weaker evidence.
Credible intervals: The 95% credible intervals (shaded regions) show our uncertainty about the true proportion. These intervals narrow with more evidence, indicating increased confidence in our estimates. This is better seen in the lower plot than in the upper one. Notice how the variance is highest when direct evidence is ambiguous (around 4 blue marbles) and lowest at the extremes (as they combine congruent evidence from both sources).

11.9 Examining Belief Distributions for Selected Scenarios

While the summary statistics give us a high-level view, examining the full posterior distributions provides deeper insight into how evidence is combined. Let’s visualize the complete probability distributions for a selected subset of scenarios:

# Function to generate Beta distributions for all components of a Bayesian model
# This function returns the prior, likelihood, and posterior distributions
# for a given scenario of blue and red marbles
simpleBayesianModel_f <- function(blue1, red1, blue2, red2) {
  # Prior parameters (uniform prior)
  alpha_prior <- 1
  beta_prior <- 1
  
  # Calculate parameters for each distribution
  # Direct evidence distribution
  alpha_direct <- alpha_prior + blue1
  beta_direct <- beta_prior + red1
  
  # Social evidence distribution
  alpha_social <- alpha_prior + blue2
  beta_social <- beta_prior + red2
  
  # Posterior distribution (combined evidence)
  alpha_post <- alpha_prior + blue1 + blue2
  beta_post <- beta_prior + red1 + red2
  
  # Create a grid of theta values (possible proportions of blue marbles)
  theta <- seq(0.001, 0.999, length.out = 200)
  
  # Calculate densities for each distribution
  prior_density <- dbeta(theta, alpha_prior, beta_prior)
  direct_density <- dbeta(theta, alpha_direct, beta_direct)
  social_density <- dbeta(theta, alpha_social, beta_social)
  posterior_density <- dbeta(theta, alpha_post, beta_post)
  
  # Return dataframe with all distributions
  return(data.frame(
    theta = theta,
    prior = prior_density,
    direct = direct_density,
    social = social_density,
    posterior = posterior_density
  ))
}

# Select a few representative scenarios
selected_scenarios <- expand_grid(
  blue1 = c(1, 4, 7),     # Different levels of direct evidence
  blue2 = c(0, 1, 2, 3)   # Different levels of social evidence
)

# Generate distributions for each scenario
distribution_data <- do.call(rbind, lapply(1:nrow(selected_scenarios), function(i) {
  blue1 <- selected_scenarios$blue1[i]
  blue2 <- selected_scenarios$blue2[i]
  
  # Generate distributions
  dist_df <- simpleBayesianModel_f(blue1, total1 - blue1, blue2, total2 - blue2)
  
  # Add scenario information
  dist_df$blue1 <- blue1
  dist_df$blue2 <- blue2
  dist_df$social_evidence <- factor(blue2,
                                    levels = c(0, 1, 2, 3),
                                    labels = c("Clear Red", "Maybe Red", "Maybe Blue", "Clear Blue"))
  return(dist_df)
}))

# Modify the plotting function
p_evidence_combination <- ggplot(distribution_data) +
  # Prior distribution with clear emphasis
  geom_line(aes(x = theta, y = prior), color = "gray50", linetype = "solid", size = 0.5) +
  
  # Posterior distribution with consistent coloring
  geom_area(aes(x = theta, y = posterior), 
            fill = "purple", 
            alpha = 0.3) +
  geom_line(aes(x = theta, y = posterior), 
            color = "purple", 
            size = 1.2) +
  
  # Direct and social evidence distributions
  geom_line(aes(x = theta, y = direct, color = "Direct Evidence"), 
            size = 1, 
            alpha = 0.7, 
            linetype = "dashed") +
  
  geom_line(aes(x = theta, y = social, color = "Social Evidence"), 
            size = 1, 
            alpha = 0.7, 
            linetype = "dashed") +
  
  # Facet by direct and social evidence levels
  facet_grid(blue2 ~ blue1, 
             labeller = labeller(
               blue1 = function(x) paste("Direct: ", x, " Blue"),
               blue2 = function(x) paste("Social: ", x, " Blue")
             )) +
  
  # Aesthetics
  scale_color_manual(values = c(
    "Direct Evidence" = "blue", 
    "Social Evidence" = "red"
  )) +
  
  # Labels and theme
  labs(
    title = "Bayesian Evidence Integration: Distribution Combination",
    subtitle = "Merging direct and social evidence into a posterior belief",
    x = "Proportion of Blue Marbles",
    y = "Probability Density",
    color = "Evidence Type"
  ) +
  theme_minimal() +
  theme(
    legend.position = "bottom",
    strip.text = element_text(size = 8),
    axis.text = element_text(size = 6)
  )

# Display the plot
print(p_evidence_combination)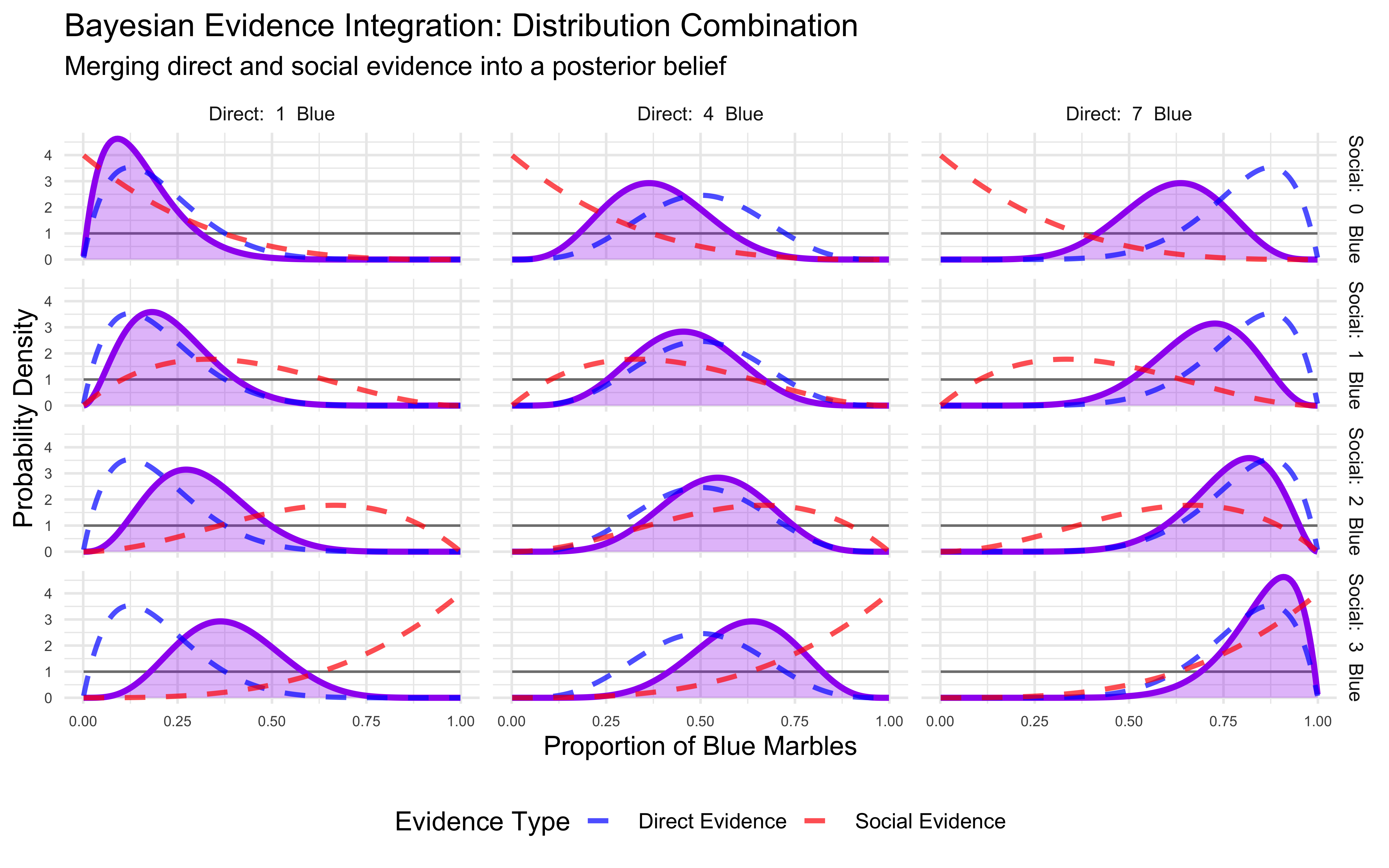

This comprehensive visualization shows how the different probability distributions interact:

Prior distribution (gray line): Our initial uniform belief about the proportion of blue marbles.
Direct evidence distribution (blue dashed line): Belief based solely on our direct observation of marbles. Notice how it becomes more concentrated with more extreme evidence (e.g., 1 or 7 blue marbles).
Social evidence distribution (red dashed line): Belief based solely on social information. This is generally less concentrated than the direct evidence distribution since it’s based on lower evidence (0-3 vs. 0-8).
Posterior distribution (purple area): The final belief that results from combining all information sources. Notice how it tends to lie between the direct and social evidence distributions, but is typically narrower than either, reflecting increased certainty from combining information, unless the evidence is in conflict.

11.10 Weighted Bayesian Integration

In real cognitive systems, people often weight information sources differently based on their reliability or relevance. Let’s implement a weighted Bayesian model that allows for differential weighting of evidence sources.

11.10.1 The Mathematical Model

Our weighted Bayesian integration model extends the simple model by introducing weight parameters for each information source:

Start with prior: Beta(α₀, β₀)
Observe direct evidence: k₁ blue marbles out of n₁ total
Observe social evidence: k₂ blue marbles out of n₂ total
Apply weights: w₁ for direct evidence, w₂ for social evidence
Posterior: Beta(α₀ + w₁·k₁ + w₂·k₂, β₀ + w₁·(n₁-k₁) + w₂·(n₂-k₂))

The weights represent the degree to which each information source influences the final belief. A weight of 2.0 means you treat that evidence as if you had observed twice as many marbles as you actually did (as more reliable than what the current evidence would warrant), while a weight of 0.5 means you treat it as half as informative. From a cognitive perspective, they might reflect judgments about reliability, relevance, or attentional focus.

11.10.2 Implementation

# Weighted Beta-Binomial model for evidence integration
#
# This function extends our basic model by allowing different weights for each
# evidence source. This can represent differences in perceived reliability,
# attention, or individual cognitive tendencies.
#
# Parameters:
#   alpha_prior, beta_prior: Prior parameters (typically 1,1 for uniform prior)
#   blue1, total1: Direct evidence (blue marbles and total)
#   blue2, total2: Social evidence (blue signals and total)
#   weight_direct, weight_social: Relative weights for each evidence source
#
# Returns:
#   List with model results and statistics
weightedBetaBinomial <- function(alpha_prior, beta_prior, 
                                blue1, total1, 
                                blue2, total2,
                                weight_direct, weight_social) {
  
  # Calculate red marbles for each source
  red1 <- total1 - blue1   # Number of red marbles in direct evidence
  red2 <- total2 - blue2   # Number of red signals in social evidence
  
  # Apply weights to evidence (this is the key step)
  # Weighting effectively scales the "sample size" of each information source
  weighted_blue1 <- blue1 * weight_direct    # Weighted blue count from direct evidence
  weighted_red1 <- red1 * weight_direct      # Weighted red count from direct evidence
  weighted_blue2 <- blue2 * weight_social    # Weighted blue count from social evidence
  weighted_red2 <- red2 * weight_social      # Weighted red count from social evidence
  
  # Calculate posterior parameters by adding weighted evidence
  alpha_post <- alpha_prior + weighted_blue1 + weighted_blue2  # Posterior alpha parameter
  beta_post <- beta_prior + weighted_red1 + weighted_red2      # Posterior beta parameter
  
  # Calculate statistics from posterior beta distribution
  expected_rate <- alpha_post / (alpha_post + beta_post)   # Mean of beta distribution
  
  # Calculate variance (lower variance = higher confidence)
  variance <- (alpha_post * beta_post) / 
              ((alpha_post + beta_post)^2 * (alpha_post + beta_post + 1))
  
  # Calculate 95% credible interval
  ci_lower <- qbeta(0.025, alpha_post, beta_post)
  ci_upper <- qbeta(0.975, alpha_post, beta_post)
  
  # Calculate decision and confidence
  decision <- ifelse(rbinom(1, 1, expected_rate) == 1, "Blue", "Red")   # Decision based on most likely color
  confidence <- 1 - (2 * sqrt(variance))                  # Confidence based on certainty
  confidence <- max(0, min(1, confidence))                # Bound between 0 and 1
  
  # Return all calculated parameters in a structured list
  return(list(
    alpha_post = alpha_post,
    beta_post = beta_post,
    expected_rate = expected_rate,
    variance = variance,
    ci_lower = ci_lower,
    ci_upper = ci_upper,
    decision = decision,
    confidence = confidence
  ))
}

11.10.3 Visualizing Weighted Bayesian Integration

Let’s create a comprehensive visualization showing how different weights affect belief formation:

# Create improved visualization using small multiples
weighted_belief_plot <- function() {
  # Define grid of parameters to visualize
  w1_values <- seq(0, 2, by = 0.2)  # Weight for source 1
  w2_values <- seq(0, 2, by = 0.2)  # Weight for source 2
  source1_values <- seq(0, 8, by = 1)  # Source 1 values
  source2_values <- seq(0, 3, by = 1)  # Source 2 values 
  
  # Generate data
  plot_data <- expand_grid(
    w1 = w1_values,
    w2 = w2_values,
    Source1 = source1_values,
    Source2 = source2_values
  ) %>%
  mutate(
    belief = pmap_dbl(list(w1, w2, Source1, Source2), function(w1, w2, s1, s2) {
      
      # Calculate Beta parameters
      alpha_prior <- 1
      beta_prior <- 1
      alpha_post <- alpha_prior + w1 * s1 + w2 * s2
      beta_post <- beta_prior + w1 * (8 - s1) + w2*(3 - s2)
      
      # Return expected value
      alpha_post / (alpha_post + beta_post)
    })
  )
  
  # Create visualization
  p <- ggplot(plot_data, aes(x = Source1, y = belief, color = Source2, group = Source2)) +
    geom_line() +
    facet_grid(w1 ~ w2, labeller = labeller(
      w1 = function(x) paste("w1 =", x),
      w2 = function(x) paste("w2 =", x)
    )) +
    scale_color_viridis_c(option = "plasma") +
    labs(
      title = "Weighted Bayesian Integration of Two Evidence Sources",
      x = "Direct Evidence (Blue Marbles)",
      y = "Belief in the next pick being a blue marble",
      color = "Social Evidence (Blue Marbles)"
    ) +
    theme_minimal() +
    theme(
      strip.background = element_rect(fill = "gray90"),
      strip.text = element_text(size = 10, face = "bold"),
      panel.grid.minor = element_blank(),
      panel.border = element_rect(color = "black", fill = NA)
    )
  
  return(p)
}

# Generate and display the plot
weighted_belief_plot()

The visualization showcases weighted Bayesian integration:

First, when both weights (w1 and w2) are low (top left panels), beliefs remain moderate regardless of the evidence values, representing high uncertainty. As weights increase (moving right and down), beliefs become more extreme, showing increased confidence in the integrated evidence.
Second, the slope of the lines indicates the relative influence of each source. Steeper slopes (bottom right panels) demonstrate that Source1 has stronger influence on belief when both weights are high, while the spacing between lines shows the impact of Source2.
Third, when weights are asymmetric (e.g., high w1 and low w2), the belief is dominated by the source with the higher weight, essentially ignoring evidence from the other source. This illustrates how selective attention to certain evidence sources can be modeled as differential weighting in a Bayesian framework.

11.10.4 Resolving Conflicting Evidence

To further understand how weighted Bayesian integration resolves conflicts between evidence sources, let’s examine two specific conflict scenarios:

# Define conflict scenarios
scenario1 <- list(blue1 = 7, total1 = 8, blue2 = 0, total2 = 3)  # Direct: blue, Social: red
scenario2 <- list(blue1 = 5, total1 = 8, blue2 = 0, total2 = 3)  # Direct: red, Social: blue

# Create function to evaluate scenarios across weight combinations
evaluate_conflict <- function(scenario) {
  weight_grid <- expand_grid(
    weight_direct =  seq(0, 2, by = 0.2),
    weight_social =  seq(0, 2, by = 0.2)
  )
  
  # Calculate results for each weight combination
  results <- pmap_dfr(weight_grid, function(weight_direct, weight_social) {
    result <- weightedBetaBinomial(
      1, 1, 
      scenario$blue1, scenario$total1, 
      scenario$blue2, scenario$total2, 
      weight_direct, weight_social
    )
    
    tibble(
      weight_direct = weight_direct,
      weight_social = weight_social,
      expected_rate = result$expected_rate,
      decision = result$decision
    )
  })
  
  return(results)
}

# Calculate results
conflict1_results <- evaluate_conflict(scenario1)
conflict2_results <- evaluate_conflict(scenario2)

# Create visualizations
p1 <- ggplot(conflict1_results, aes(x = weight_direct, y = weight_social)) +
  geom_tile(aes(fill = expected_rate)) +
  geom_contour(aes(z = expected_rate), breaks = 0.5, color = "black", size = 1) +
  scale_fill_gradient2(
    low = "red", mid = "white", high = "blue", 
    midpoint = 0.5, limits = c(0, 1)
  ) +
  labs(
    title = "Scenario 1: Strong Direct Evidence for Blue (7 out of 8) \nvs. Strong Social Evidence for Red (0/3)",
    subtitle = "Black line shows decision boundary (expected rate = 0.5)",
    x = "Weight for Direct Evidence",
    y = "Weight for Social Evidence",
    fill = "Expected\nRate"
  ) +
  theme_minimal() +
  coord_fixed()

p2 <- ggplot(conflict2_results, aes(x = weight_direct, y = weight_social)) +
  geom_tile(aes(fill = expected_rate)) +
  geom_contour(aes(z = expected_rate), breaks = 0.5, color = "black", size = 1) +
  scale_fill_gradient2(
    low = "red", mid = "white", high = "blue", 
    midpoint = 0.5, limits = c(0, 1)
  ) +
  labs(
    title = "Scenario 1: Weak Direct Evidence for Blue (5 out of 8) \nvs. Strong Social Evidence for Red (0/3)",
    subtitle = "Black line shows decision boundary (expected rate = 0.5)",
    x = "Weight for Direct Evidence",
    y = "Weight for Social Evidence",
    fill = "Expected\nRate"
  ) +
  theme_minimal() +
  coord_fixed()

# Display plots
p1 / p2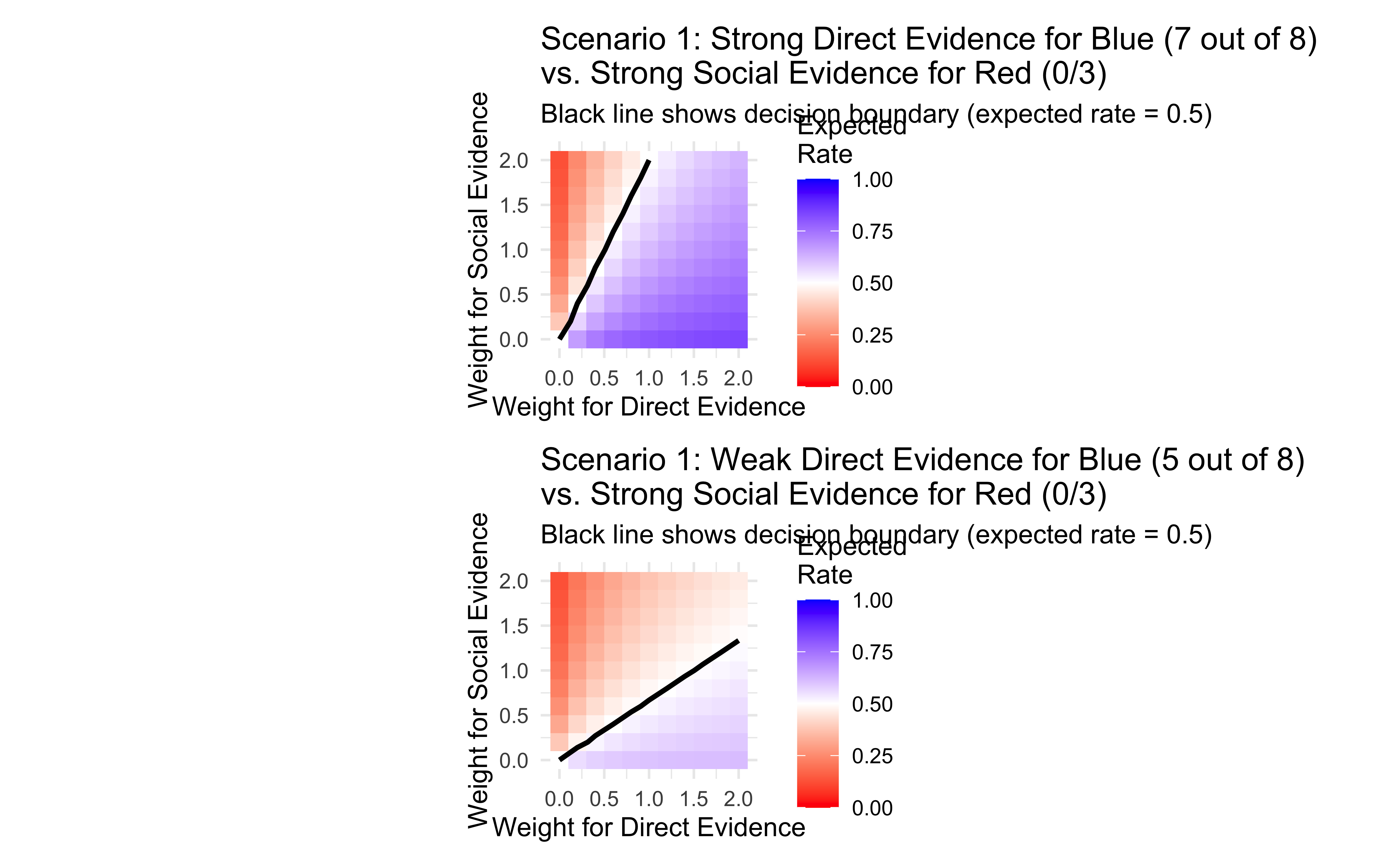

These visualizations illustrate how different weight combinations resolve conflicts between evidence sources:

Decision boundary: The black line represents combinations of weights that lead to equal evidence for red and blue (expected rate = 0.5). Weight combinations above this line lead to a “blue” decision, while those below lead to a “red” decision.
Relative evidence strength: The slope of the decision boundary reflects the relative strength of the evidence sources. A steeper slope indicates that direct evidence is stronger relative to social evidence.
Individual differences: Different individuals might give different weights to evidence sources, leading to different decisions even when faced with identical evidence. This provides a mechanistic explanation for individual variation in decision-making.

11.11 Common Misinterpretations

11.11.1 Weight Interpretation

Weights effectively scale the relative importance of each source of evidence. A weight of 0 means ignoring that evidence source entirely. A weight of 1 means treating the evidence as observed, at face value. Weights above 1 amplify the evidence, while weights below 1 dampen it. A negative weight would make the agent invert the direction of the evidence (if more evidence for red, they’d tend to pick blue). Remember that weights moderate the evidence, so a strong weight doesn’t guarantee a strong influence if the evidence itself is weak.

11.11.2 Integration vs. Averaging

Bayesian integration is not simply the averaging of evidence across sources, because it naturally includes how precise the evidence is (how narrow the distribution). Normally, this would happen when we multiply the distributions involved. The Beta-Binomial model handles this automatically by incorporating sample sizes (the n of marbles).

11.11.3 Interpreting Confidence

There is something tricky in this model when it comes to confidence. We can say that a belief that the next sample is going to be blue with a 0.8 (average) probability more confident than one with a 0.6 (average) probability. We can also say that a belief that the next sample is going to be blue with a 0.8 (95% CIs 0.5-1) probability is less confident than a belief with a 0.6 (95% CIs 0.55-0.65) probability. We need to keep these two aspects separate. The first one is about the average probability, the second one is about the uncertainty around that average probability. In the code above we only call the second confidence and use entropy of the posterior distribution to quantify it.

11.12 Simulating Agents with Different Evidence Weighting Strategies

To prepare for our model fitting, we’ll simulate three distinct agents:

Balanced Agent: This agent treats both direct and social evidence at face value, applying equal weights (w_direct = 1.0, w_social = 1.0). This represents an unbiased integration of information.
Self-Focused Agent: This agent overweights their own direct evidence (w_direct = 1.5) while underweighting social evidence (w_social = 0.5). This represents someone who trusts their own observations more than information from others.
Socially-Influenced Agent: This agent does the opposite, overweighting social evidence (w_social = 2.0) while underweighting their own direct evidence (w_direct = 0.7). This might represent someone who is highly responsive to social information.

Let’s generate decisions for these three agents in an experiment exposing them to all possible evidence combinations and visualize how their different weighting strategies affect their beliefs and choices.

# Simulation of agents with different weighting strategies
# This code generates decisions for three agents with different approaches to weighting evidence

# Define our three agent types with their respective weights
agents <- tibble(
  agent_type = c("Balanced", "Self-Focused", "Socially-Influenced"),
  weight_direct = c(1.0, 1.5, 0.7),   # Weight for direct evidence
  weight_social = c(1.0, 0.5, 2.0)    # Weight for social evidence
)

# Create all possible evidence combinations
# Direct evidence: 0-8 blue marbles out of 8 total
# Social evidence: 0-3 signals (representing confidence levels)
evidence_combinations <- expand_grid(
  blue1 = 0:8,     # Direct evidence: number of blue marbles seen
  blue2 = 0:3      # Social evidence: strength of blue evidence
) %>% mutate(
  total1 = 8,      # Total marbles in direct evidence
  total2 = 3       # Total strength units in social evidence
)

generate_agent_decisions <- function(weight_direct, weight_social, evidence_df, n_samples = 5) {
  # Create a data frame that repeats each evidence combination n_samples times
  repeated_evidence <- evidence_df %>%
    slice(rep(1:n(), each = n_samples)) %>%
    # Add a sample_id to distinguish between repetitions of the same combination
    group_by(blue1, blue2, total1, total2) %>%
    mutate(sample_id = 1:n()) %>%
    ungroup()
  
  # Apply our weighted Bayesian model to each evidence combination
  decisions <- pmap_dfr(repeated_evidence, function(blue1, blue2, total1, total2, sample_id) {
    # Calculate Bayesian integration with the agent's specific weights
    result <- weightedBetaBinomial(
      alpha_prior = 1, beta_prior = 1,
      blue1 = blue1, total1 = total1,
      blue2 = blue2, total2 = total2,
      weight_direct = weight_direct,
      weight_social = weight_social
    )
    
    # Return key decision metrics
    tibble(
      sample_id = sample_id,
      blue1 = blue1,
      blue2 = blue2,
      total1 = total1,
      total2 = total2,
      expected_rate = result$expected_rate,   # Probability the next marble is blue
      choice = result$decision,               # Final decision (Blue or Red)
      choice_binary = ifelse(result$decision == "Blue", 1, 0),
      confidence = result$confidence          # Confidence in decision
    )
  })
  
  return(decisions)
}

# When generating data for weighted Bayesian model simulation
simulation_results <- map_dfr(1:nrow(agents), function(i) {
  # Extract this agent's parameters
  agent_data <- agents[i, ]
  
  # Generate decisions for this agent with multiple samples
  decisions <- generate_agent_decisions(
    agent_data$weight_direct,
    agent_data$weight_social,
    evidence_combinations,
    n_samples = 5  # Generate 5 samples per evidence combination
  )
  
  # Add agent identifier
  decisions$agent_type <- agent_data$agent_type
  
  return(decisions)
})

# Add descriptive labels for visualization
simulation_results <- simulation_results %>%
  mutate(
    # Create descriptive labels for social evidence
    social_evidence = factor(
      blue2,
      levels = 0:3,
      labels = c("Clear Red", "Maybe Red", "Maybe Blue", "Clear Blue")
    ),
    # Create factor for agent type to control plotting order
    agent_type = factor(
      agent_type,
      levels = c("Balanced", "Self-Focused", "Socially-Influenced")
    )
  )

# Let's examine a sample of the generated data
head(simulation_results)

## # A tibble: 6 × 11
##   sample_id blue1 blue2 total1 total2 expected_rate choice choice_binary confidence
##       <int> <int> <int>  <dbl>  <dbl>         <dbl> <chr>          <dbl>      <dbl>
## 1         1     0     0      8      3        0.0769 Red                0      0.858
## 2         2     0     0      8      3        0.0769 Red                0      0.858
## 3         3     0     0      8      3        0.0769 Red                0      0.858
## 4         4     0     0      8      3        0.0769 Red                0      0.858
## 5         5     0     0      8      3        0.0769 Red                0      0.858
## 6         1     0     1      8      3        0.154  Red                0      0.807
## # ℹ 2 more variables: agent_type <fct>, social_evidence <fct>

Now let’s create visualizations to compare how these different agents make decisions based on the same evidence:

# Visualization 1: Expected probability across evidence combinations
p1 <- ggplot(simulation_results, 
             aes(x = blue1, y = expected_rate, color = social_evidence, group = social_evidence)) +
  # Draw a line for each social evidence level
  geom_line(size = 1) +
  # Add points to show discrete evidence combinations
  geom_point(size = 2) +
  # Add a reference line at 0.5 (decision boundary)
  geom_hline(yintercept = 0.5, linetype = "dashed", color = "gray50") +
  # Facet by agent type
  facet_wrap(~ agent_type, ncol = 1) +
  # Customize colors and labels
  scale_color_brewer(palette = "Set1") +
  scale_x_continuous(breaks = 0:8) +
  labs(
    title = "How Different Agents Integrate Evidence",
    subtitle = "Expected probability of blue marble across evidence combinations",
    x = "Number of Blue Marbles in Direct Sample (out of 8)",
    y = "Expected Probability of Blue",
    color = "Social Evidence"
  ) +
  theme_bw() +
  theme(legend.position = "bottom")

# Visualization 2: Decision boundaries for each agent
# Create a simplified dataset showing just the decision (Blue/Red)
decision_data <- simulation_results %>%
  mutate(decision_value = ifelse(choice == "Blue", 1, 0))

p2 <- ggplot(decision_data, aes(x = blue1, y = blue2)) +
  # Create tiles colored by decision
  geom_tile(aes(fill = choice)) +
  # Add decision boundary contour line
  stat_contour(aes(z = decision_value), breaks = 0.5, color = "black", size = 1) +
  # Facet by agent type
  facet_wrap(~ agent_type) +
  # Customize colors and labels
  scale_fill_manual(values = c("Red" = "firebrick", "Blue" = "royalblue")) +
  scale_x_continuous(breaks = 0:8) +
  scale_y_continuous(breaks = 0:3) +
  labs(
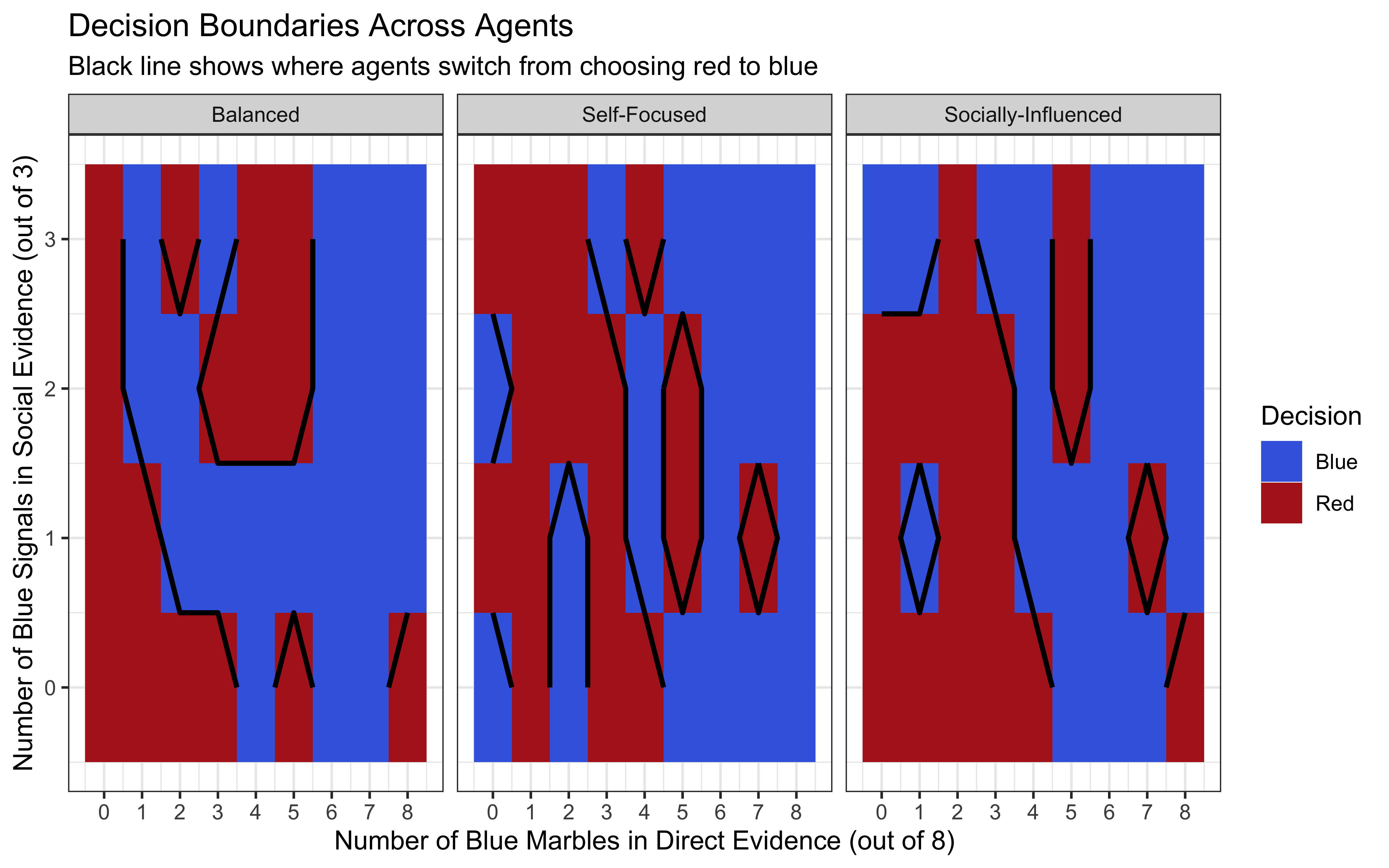
    title = "Decision Boundaries Across Agents",
    subtitle = "Black line shows where agents switch from choosing red to blue",
    x = "Number of Blue Marbles in Direct Evidence (out of 8)",
    y = "Number of Blue Signals in Social Evidence (out of 3)",
    fill = "Decision"
  ) +
  theme_bw()

# Visualization 3: Confidence levels
p3 <- ggplot(simulation_results, aes(x = blue1, y = confidence, color = social_evidence, group = social_evidence)) +
  geom_line(size = 1) +
  geom_point(size = 2) +
  facet_wrap(~ agent_type, ncol = 1) +
  scale_color_brewer(palette = "Set1") +
  scale_x_continuous(breaks = 0:8) +
  labs(
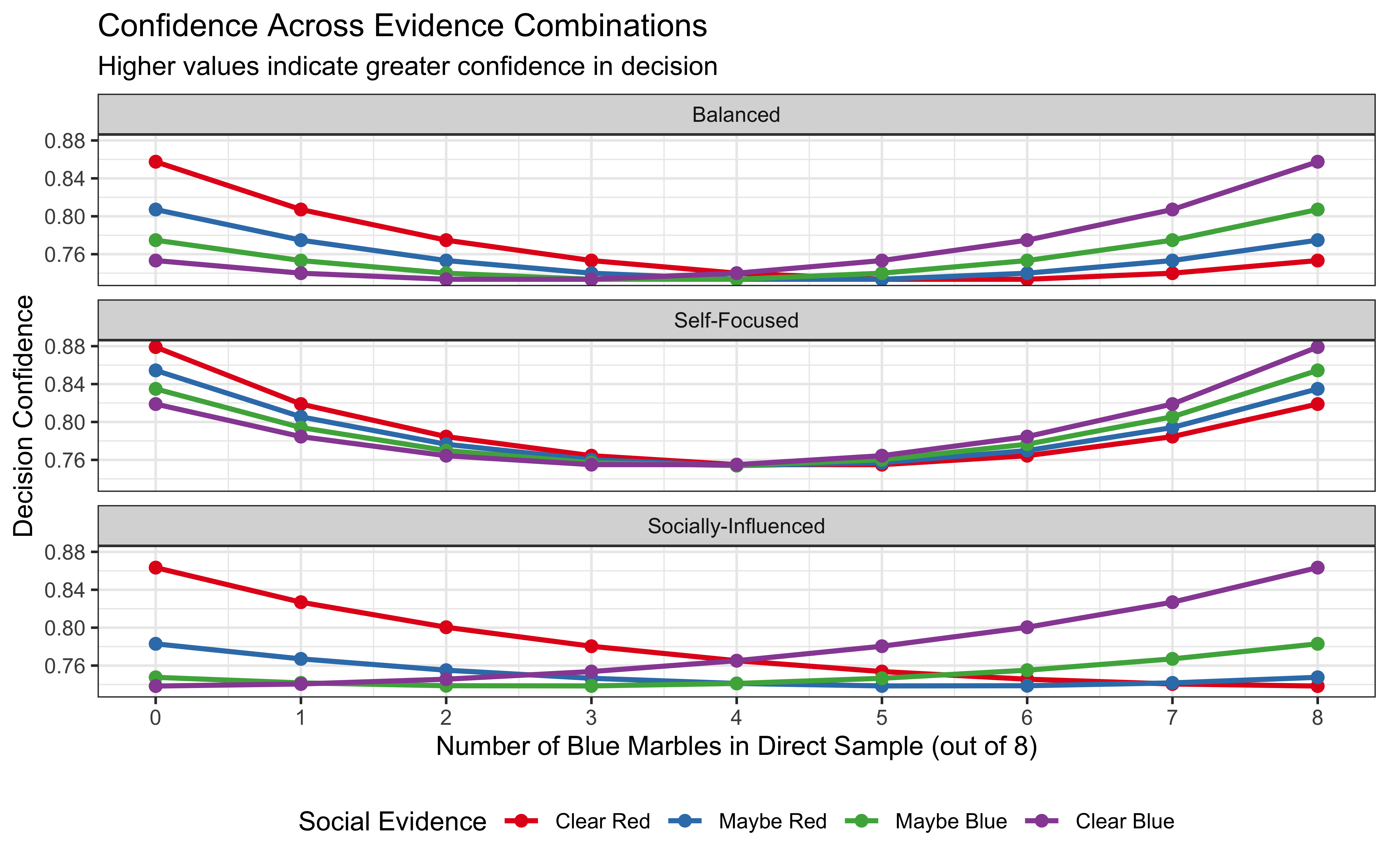
    title = "Confidence Across Evidence Combinations",
    subtitle = "Higher values indicate greater confidence in decision",
    x = "Number of Blue Marbles in Direct Sample (out of 8)",
    y = "Decision Confidence",
    color = "Social Evidence"
  ) +
  theme_bw() +
  theme(legend.position = "bottom")

# Display the visualizations
p1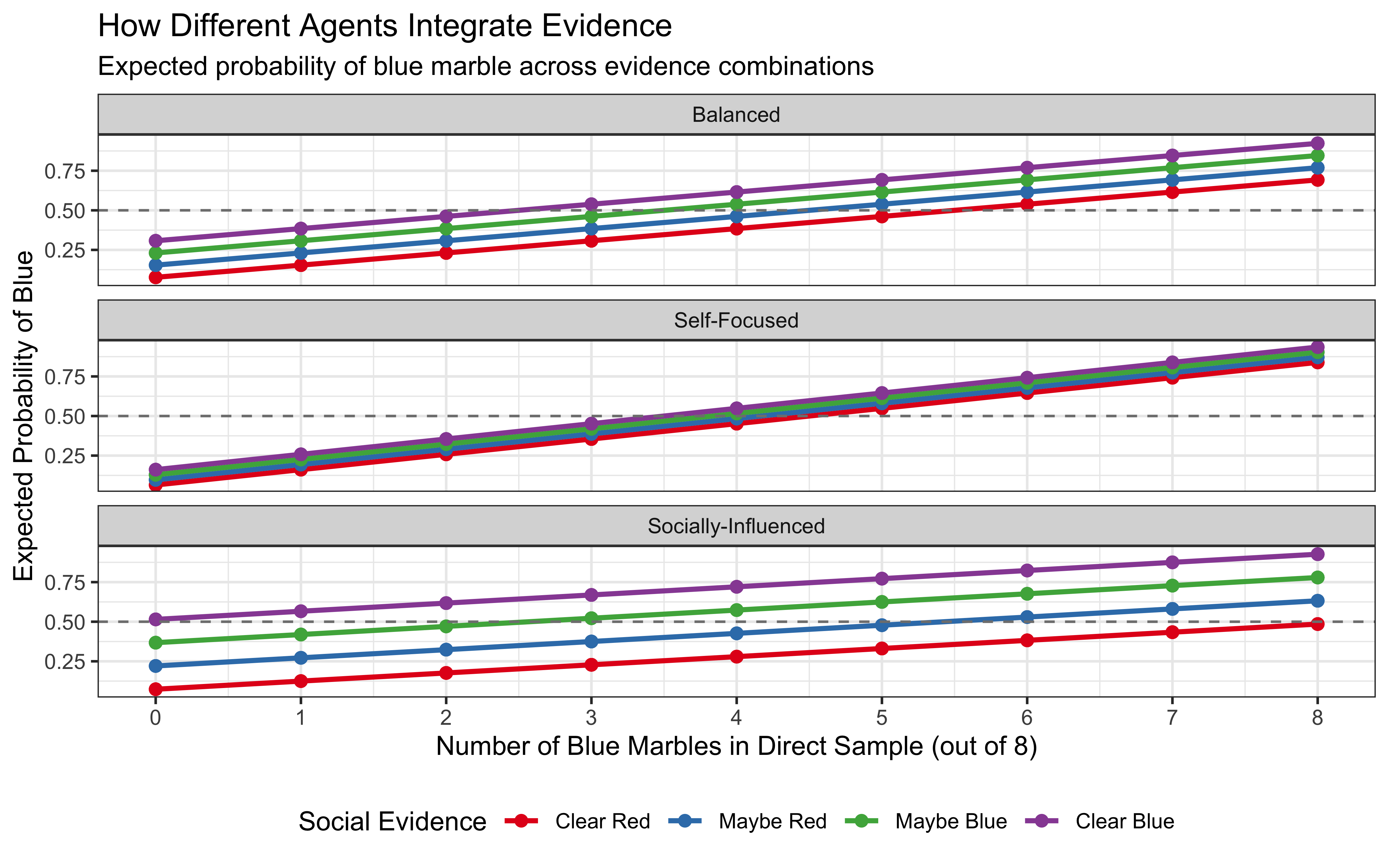

p2

p3

11.13 Key Observations from the Simulation

Our simulation highlights several important aspects of Bayesian evidence integration with different weighting strategies:

Evidence Thresholds: The decision boundaries (Visualization 2) clearly show how much evidence each agent requires to switch from choosing red to blue. The Self-Focused agent needs less direct evidence when social evidence supports blue, compared to the Socially-Influenced agent.
Influence of Social Evidence: In the first visualization, we can observe how the lines for different social evidence levels are spaced. For the Socially-Influenced agent, these lines are widely spaced, indicating that social evidence strongly affects their beliefs. For the Self-Focused agent, the lines are closer together, showing less impact from social evidence.
Confidence Patterns: The third visualization reveals how confidence varies across evidence combinations and agent types. All agents are most confident when evidence is strong and consistent across sources, but they differ in how they handle conflicting evidence.
Decision Regions: The Self-Focused agent has a larger region where they choose blue based primarily on direct evidence, while the Socially-Influenced agent has more regions where social evidence can override moderate direct evidence.

These patterns highlight the profound impact that evidence weighting can have on decision-making, even when agents are all using the same underlying Bayesian integration mechanism. In the next section, we’ll implement these agents in Stan to perform more sophisticated parameter estimation.

Now, let’s define our Stan models to implement: a simple bayesian agent (equivalent to assuming both weights to be 1); and a weighted bayesian agent (explicitly inferring weights for direct and social evidence).

# Simple Beta-Binomial Stan model (no weights)
SimpleAgent_stan <- "
// Bayesian integration model relying on a beta-binomial distribution
// to preserve all uncertainty
// All evidence is taken at face value (equal weights)
data {
  int<lower=1> N;                      // Number of decisions
  array[N] int<lower=0, upper=1> choice; // Choices (0=red, 1=blue)
  array[N] int<lower=0> blue1;         // Direct evidence (blue marbles)
  array[N] int<lower=0> total1;        // Total direct evidence (total marbles)
  array[N] int<lower=0> blue2;         // Social evidence (blue signals)
  array[N] int<lower=0> total2;        // Total social evidence (total signals)
}

parameters{
  real<lower = 0> alpha_prior;                    // Prior alpha parameter
  real<lower = 0> beta_prior;                     // Prior beta parameter
}

model {

  target += lognormal_lpdf(alpha_prior | 0, 1); // Prior on alpha_prior, the agent bias towards blue
  target += lognormal_lpdf(beta_prior | 0, 1);  // Prior on beta_prior, the agent bias towards red

  // Each observation is a separate decision
  for (i in 1:N) {
    // Calculate Beta parameters for posterior belief distribution
    real alpha_post = alpha_prior + blue1[i] + blue2[i];
    real beta_post = beta_prior + (total1[i] - blue1[i]) + (total2[i] - blue2[i]);
    
    // Use beta_binomial distribution which integrates over all possible values
    // of the rate parameter weighted by their posterior probability
    target += beta_binomial_lpmf(choice[i] | 1, alpha_post, beta_post);
  }
}

generated quantities {
  // Log likelihood for model comparison
  vector[N] log_lik;
  
  // Prior and posterior predictive checks
  array[N] int prior_pred_choice;
  array[N] int posterior_pred_choice;
  
  for (i in 1:N) {
    // For prior predictions, use uniform prior (Beta(1,1))
    prior_pred_choice[i] = beta_binomial_rng(1, 1, 1);
    
    // For posterior predictions, use integrated evidence
    real alpha_post = alpha_prior + blue1[i] + blue2[i];
    real beta_post = beta_prior + (total1[i] - blue1[i]) + (total2[i] - blue2[i]);
    
    // Generate predictions using the complete beta-binomial model
    posterior_pred_choice[i] = beta_binomial_rng(1, alpha_post, beta_post);
    
    // Log likelihood calculation using beta-binomial
    log_lik[i] = beta_binomial_lpmf(choice[i] | 1, alpha_post, beta_post);
  }
}
"

# Weighted Beta-Binomial Stan model
WeightedAgent_stan <- "
data {
  int<lower=1> N;                        // Number of decisions
  array[N] int<lower=0, upper=1> choice; // Choices (0=red, 1=blue)
  array[N] int<lower=0> blue1;           // Direct evidence (blue marbles)
  array[N] int<lower=0> total1;          // Total direct evidence
  array[N] int<lower=0> blue2;           // Social evidence (blue signals)
  array[N] int<lower=0> total2;          // Total social evidence
}

parameters {
  real<lower = 0> alpha_prior;                    // Prior alpha parameter
  real<lower = 0> beta_prior;                     // Prior beta parameter
  real<lower=0> total_weight;         // Total influence of all evidence
  real<lower=0, upper=1> weight_prop; // Proportion of weight for direct evidence
}

transformed parameters {
  real<lower=0> weight_direct = total_weight * weight_prop;
  real<lower=0> weight_social = total_weight * (1 - weight_prop);
}

model {
  // Priors
  target += lognormal_lpdf(alpha_prior | 0, 1); // Prior on alpha_prior
  target += lognormal_lpdf(beta_prior | 0, 1);  // Prior on beta_prior
  target += lognormal_lpdf(total_weight | .8, .4);  // Centered around 2 with reasonable spread and always positive
  target += beta_lpdf(weight_prop | 1, 1);    // Uniform prior on proportion
  
  // Each observation is a separate decision
  for (i in 1:N) {
    // For this specific decision:
    real weighted_blue1 = blue1[i] * weight_direct;
    real weighted_red1 = (total1[i] - blue1[i]) * weight_direct;
    real weighted_blue2 = blue2[i] * weight_social;
    real weighted_red2 = (total2[i] - blue2[i]) * weight_social;
    
    // Calculate Beta parameters for this decision
    real alpha_post = alpha_prior + weighted_blue1 + weighted_blue2;
    real beta_post = beta_prior + weighted_red1 + weighted_red2;
    
    // Use beta_binomial distribution to integrate over the full posterior
    target += beta_binomial_lpmf(choice[i] | 1, alpha_post, beta_post);
  }
}

generated quantities {
  // Log likelihood and predictions
  vector[N] log_lik;
  array[N] int posterior_pred_choice;
  array[N] int prior_pred_choice;
  
  // Sample the agent's preconceptions
  real alpha_prior_prior = lognormal_rng(0, 1);
  real beta_prior_prior = lognormal_rng(0, 1);
  
  // Sample from priors for the reparameterized model
  real<lower = 0> total_weight_prior = lognormal_rng(.8, .4);
  real weight_prop_prior = beta_rng(1, 1);
  
  // Derive the implied direct and social weights from the prior samples
  real weight_direct_prior = total_weight_prior * weight_prop_prior;
  real weight_social_prior = total_weight_prior * (1 - weight_prop_prior);
  
  // Posterior predictions and log-likelihood
  for (i in 1:N) {
    // Posterior predictions using the weighted evidence
    real weighted_blue1 = blue1[i] * weight_direct;
    real weighted_red1 = (total1[i] - blue1[i]) * weight_direct;
    real weighted_blue2 = blue2[i] * weight_social;
    real weighted_red2 = (total2[i] - blue2[i]) * weight_social;
    
    real alpha_post = alpha_prior + weighted_blue1 + weighted_blue2;
    real beta_post = beta_prior + weighted_red1 + weighted_red2;
    
    // Log likelihood using beta_binomial
    log_lik[i] = beta_binomial_lpmf(choice[i] | 1, alpha_post, beta_post);
    
    // Generate predictions from the full posterior
    posterior_pred_choice[i] = beta_binomial_rng(1, alpha_post, beta_post);
    
    // Prior predictions using the prior-derived weights
    real prior_weighted_blue1 = blue1[i] * weight_direct_prior;
    real prior_weighted_red1 = (total1[i] - blue1[i]) * weight_direct_prior;
    real prior_weighted_blue2 = blue2[i] * weight_social_prior;
    real prior_weighted_red2 = (total2[i] - blue2[i]) * weight_social_prior;
    
    real alpha_prior_preds = alpha_prior + prior_weighted_blue1 + prior_weighted_blue2;
    real beta_prior_preds = beta_prior + prior_weighted_red1 + prior_weighted_red2;
    
    // Generate predictions from the prior
    prior_pred_choice[i] = beta_binomial_rng(1, alpha_prior, beta_prior);
  }
}
"

# Write the models to files
write_stan_file(
  SimpleAgent_stan,
  dir = "stan/",
  basename = "W10 _beta_binomial.stan"
)

## [1] "/Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/stan/W10 _beta_binomial.stan"

write_stan_file(
  WeightedAgent_stan,
  dir = "stan/",
  basename = "W10 _weighted_beta_binomial.stan"
)

## [1] "/Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/stan/W10 _weighted_beta_binomial.stan"

# Prepare simulation data for Stan fitting
# Convert 'Blue' and 'Red' choices to binary format (1 for Blue, 0 for Red)
sim_data_for_stan <- simulation_results %>%
  mutate(
    choice_binary = as.integer(choice == "Blue"),
    total1 = 8,  # Total marbles in direct evidence (constant)
    total2 = 3   # Total signals in social evidence (constant)
  )

# Split data by agent type
balanced_data <- sim_data_for_stan %>% filter(agent_type == "Balanced")
self_focused_data <- sim_data_for_stan %>% filter(agent_type == "Self-Focused")
socially_influenced_data <- sim_data_for_stan %>% filter(agent_type == "Socially-Influenced")

# Function to prepare data for Stan
prepare_stan_data <- function(df) {
  list(
    N = nrow(df),
    choice = df$choice_binary,
    blue1 = df$blue1,
    total1 = df$total1,
    blue2 = df$blue2,
    total2 = df$total2
  )
}

# Prepare Stan data for each agent
stan_data_balanced <- prepare_stan_data(balanced_data)
stan_data_self_focused <- prepare_stan_data(self_focused_data)
stan_data_socially_influenced <- prepare_stan_data(socially_influenced_data)

# Compile the Stan models
file_simple <- file.path("stan/W10 _beta_binomial.stan")
file_weighted <- file.path("stan/W10 _weighted_beta_binomial.stan")

# Check if we need to regenerate simulation results
if (regenerate_simulations) {
  # Compile models
  mod_simple <- cmdstan_model(file_simple, cpp_options = list(stan_threads = TRUE))
  mod_weighted <- cmdstan_model(file_weighted, cpp_options = list(stan_threads = TRUE))
  
  # Fit simple model to each agent's data
  fit_simple_balanced <- mod_simple$sample(
    data = stan_data_balanced,
    seed = 123,
    chains = 2,
    parallel_chains = 2,
    threads_per_chain = 1,
    iter_warmup = 1000,
    iter_sampling = 1000,
    refresh = 0  # Set to 500 or so to see progress
  )
  
  fit_simple_self_focused <- mod_simple$sample(
    data = stan_data_self_focused,
    seed = 124,
    chains = 2,
    parallel_chains = 2,
    threads_per_chain = 1,
    iter_warmup = 1000,
    iter_sampling = 1000,
    refresh = 0
  )
  
  fit_simple_socially_influenced <- mod_simple$sample(
    data = stan_data_socially_influenced,
    seed = 125,
    chains = 2,
    parallel_chains = 2,
    threads_per_chain = 1,
    iter_warmup = 1000,
    iter_sampling = 1000,
    refresh = 0
  )
  
  # Fit weighted model to each agent's data
  fit_weighted_balanced <- mod_weighted$sample(
    data = stan_data_balanced,
    seed = 124,
    chains = 2,
    parallel_chains = 2,
    threads_per_chain = 1,
    iter_warmup = 1000,
    iter_sampling = 1000,
    refresh = 0
  )
  
  fit_weighted_self_focused <- mod_weighted$sample(
    data = stan_data_self_focused,
    seed = 127,
    chains = 2,
    parallel_chains = 2,
    threads_per_chain = 1,
    iter_warmup = 1000,
    iter_sampling = 1000,
    refresh = 0
  )
  
  fit_weighted_socially_influenced <- mod_weighted$sample(
    data = stan_data_socially_influenced,
    seed = 128,
    chains = 2,
    parallel_chains = 2,
    threads_per_chain = 1,
    iter_warmup = 1000,
    iter_sampling = 1000,
    refresh = 0
  )
  
  # Save model fits for future use
  fit_simple_balanced$save_object("simmodels/fit_simple_balanced.rds")
  fit_simple_self_focused$save_object("simmodels/fit_simple_self_focused.rds")
  fit_simple_socially_influenced$save_object("simmodels/fit_simple_socially_influenced.rds")
  fit_weighted_balanced$save_object("simmodels/fit_weighted_balanced.rds")
  fit_weighted_self_focused$save_object("simmodels/fit_weighted_self_focused.rds")
  fit_weighted_socially_influenced$save_object("simmodels/fit_weighted_socially_influenced.rds")
  
  cat("Generated and saved new model fits\n")
} else {
  # Load existing model fits
  fit_simple_balanced <- readRDS("simmodels/fit_simple_balanced.rds")
  fit_simple_self_focused <- readRDS("simmodels/fit_simple_self_focused.rds")
  fit_simple_socially_influenced <- readRDS("simmodels/fit_simple_socially_influenced.rds")
  fit_weighted_balanced <- readRDS("simmodels/fit_weighted_balanced.rds")
  fit_weighted_self_focused <- readRDS("simmodels/fit_weighted_self_focused.rds")
  fit_weighted_socially_influenced <- readRDS("simmodels/fit_weighted_socially_influenced.rds")
  
  cat("Loaded existing model fits\n")
}

## Loaded existing model fits

11.14 Model Quality Checks

11.14.1 Overview

Model quality checks are crucial for understanding how well our Bayesian models capture the underlying data-generating process. We’ll use three primary techniques:

Prior Predictive Checks
Posterior Predictive Checks
Prior-Posterior Update Visualization

# Function to create trace and rank plots for a model
create_diagnostic_plots <- function(fit, model_name) {
  # Extract posterior draws
  draws <- as_draws_df(fit$draws()) 
  
  trace_data <- data.frame(
    Iteration = rep(1:(nrow(draws)/length(unique(draws$.chain))), 
                    length(unique(draws$.chain))),
    Chain = draws$.chain,
    weight_direct = draws$weight_direct,
    weight_social = draws$weight_social,
    total_weight = draws$total_weight,
    weight_prop = draws$weight_prop
  )
  
  # Create trace plot
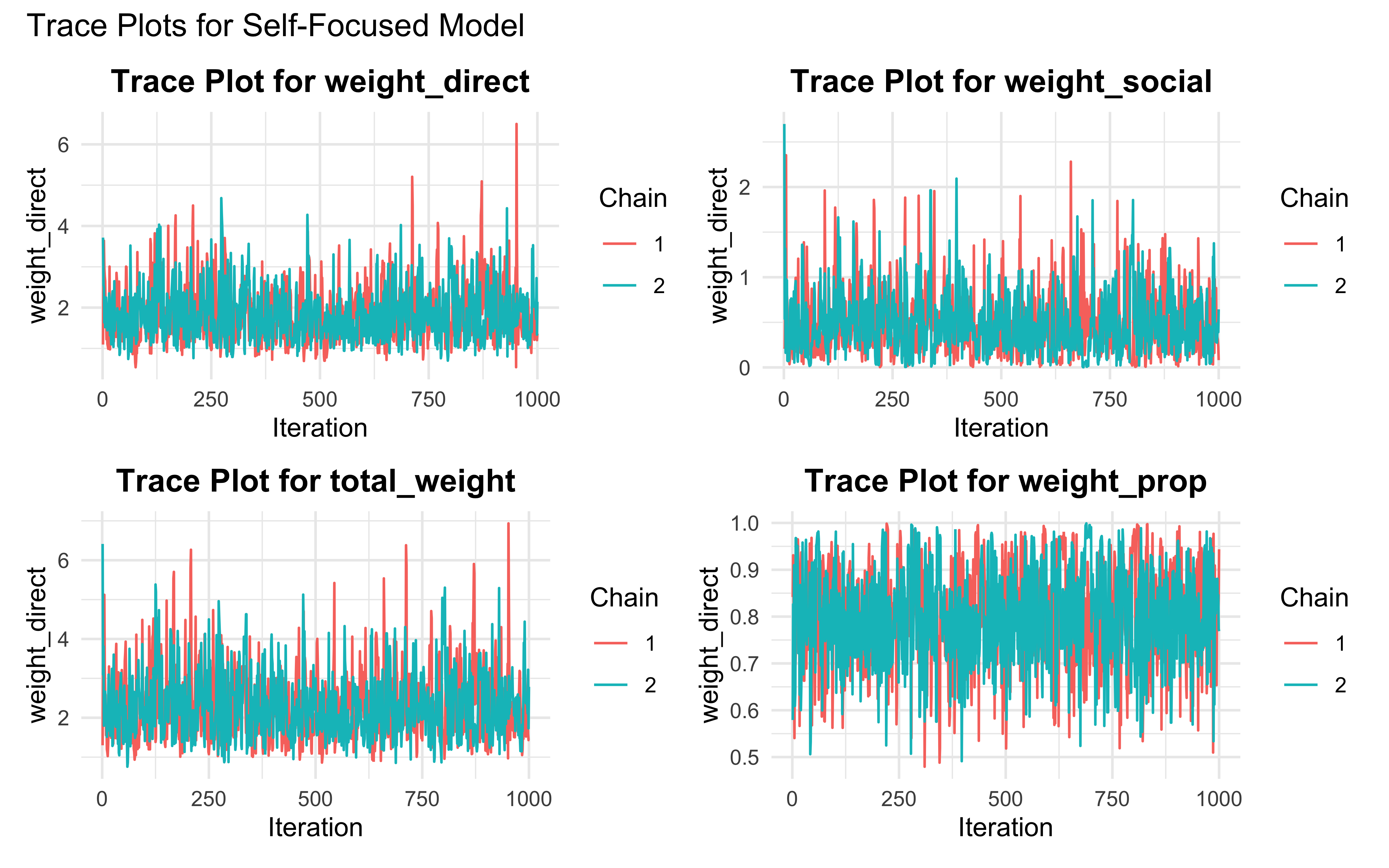
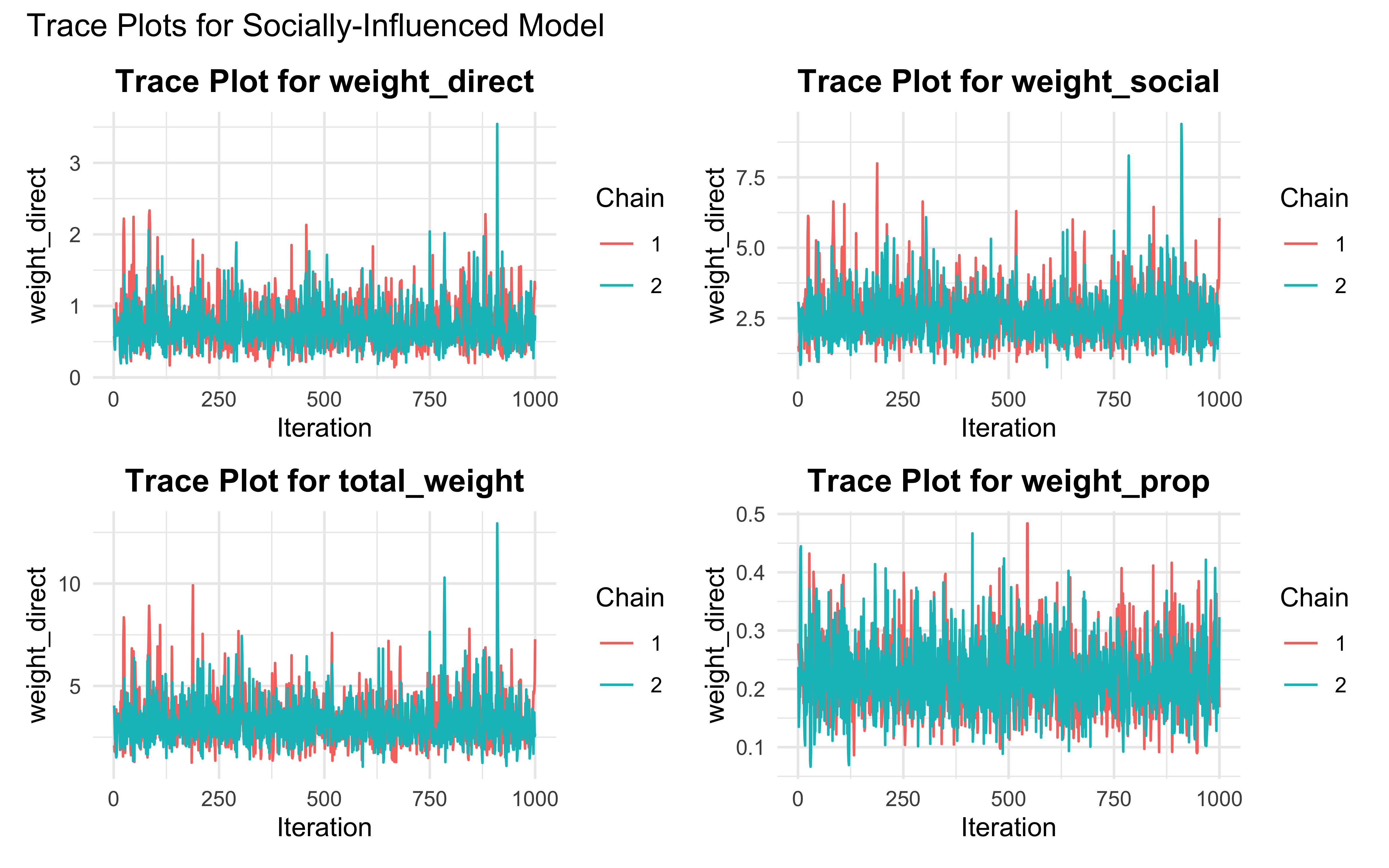
  trace_plot1 <- ggplot(trace_data, aes(x = Iteration, y = weight_direct, color = factor(Chain))) +
    geom_line() +
    labs(title = paste("Trace Plot for weight_direct"),
         x = "Iteration",
         y = "weight_direct",
         color = "Chain") +
    theme_minimal() +
    theme(plot.title = element_text(hjust = 0.5, face = "bold"))
  
  trace_plot2 <- ggplot(trace_data, aes(x = Iteration, y = weight_social, color = factor(Chain))) +
    geom_line() +
    labs(title = paste("Trace Plot for weight_social"),
         x = "Iteration",
         y = "weight_direct",
         color = "Chain") +
    theme_minimal() +
    theme(plot.title = element_text(hjust = 0.5, face = "bold"))
  
  trace_plot3 <- ggplot(trace_data, aes(x = Iteration, y = total_weight, color = factor(Chain))) +
    geom_line() +
    labs(title = paste("Trace Plot for total_weight"),
         x = "Iteration",
         y = "weight_direct",
         color = "Chain") +
    theme_minimal() +
    theme(plot.title = element_text(hjust = 0.5, face = "bold"))
  
  trace_plot4 <- ggplot(trace_data, aes(x = Iteration, y = weight_prop, color = factor(Chain))) +
    geom_line() +
    labs(title = paste("Trace Plot for weight_prop"),
         x = "Iteration",
         y = "weight_direct",
         color = "Chain") +
    theme_minimal() +
    theme(plot.title = element_text(hjust = 0.5, face = "bold"))
  
  # Combine plots using patchwork
  combined_trace_plot <- (trace_plot1 + trace_plot2) / (trace_plot3 + trace_plot4) +
    plot_annotation(title = paste("Trace Plots for", model_name))
  
  
  # Return the plots
  return(combined_trace_plot)
}

# Generate diagnostic plots for each model
create_diagnostic_plots(fit_weighted_balanced, "Balanced Model")

create_diagnostic_plots(fit_weighted_self_focused, "Self-Focused Model")

create_diagnostic_plots(fit_weighted_socially_influenced, "Socially-Influenced Model")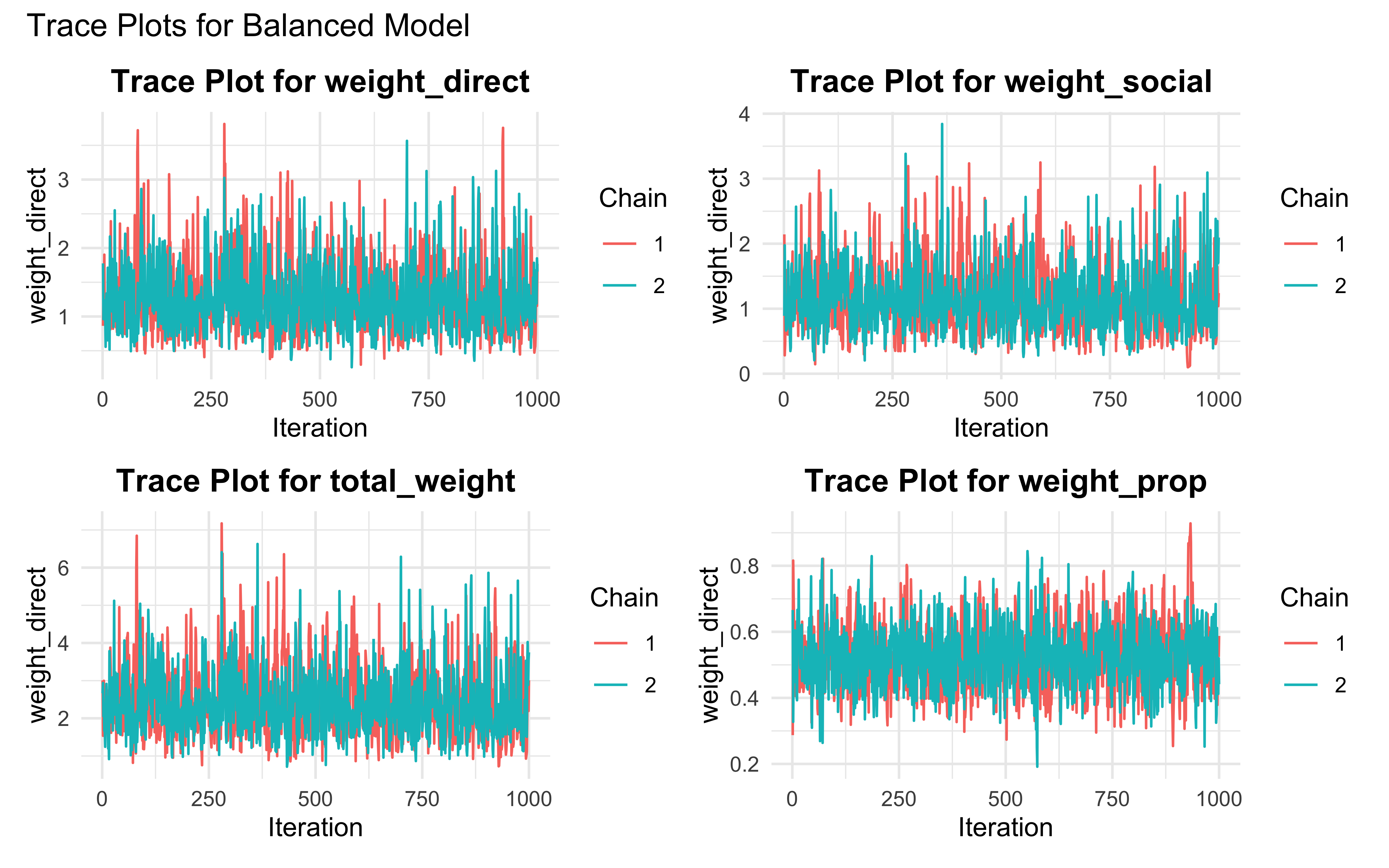

11.14.2 Prior and Posterior Predictive Checks

Prior predictive checks help us understand what our model assumes about the world before seeing any data. They answer the question: “What kind of data would we expect to see if we only used our prior beliefs?” Posterior predictive checks are the same, but after having seen the data. This helps us assess whether the model can generate data that looks similar to our observed data.

plot_predictive_checks <- function(stan_fit, 
                                   simulation_results, 
                                   model_name = "Simple Balanced", 
                                   param_name = "prior_pred_choice") {
  # Extract predictive samples
  pred_samples <- stan_fit$draws(param_name, format = "data.frame")
  
  # Get the number of samples and observations
  n_samples <- nrow(pred_samples)
  n_obs <- ncol(pred_samples) - 3  # Subtract chain, iteration, and draw columns
  
  # Convert to long format
  long_pred <- pred_samples %>%
    dplyr::select(-.chain, -.iteration, -.draw) %>%  # Remove metadata columns
    pivot_longer(
      cols = everything(),
      names_to = "obs_id",
      values_to = "choice"
    ) %>%
    mutate(obs_id = parse_number(obs_id))  # Extract observation number
  
  # Join with the original simulation data to get evidence levels
  # First, add an observation ID to the simulation data
  sim_with_id <- simulation_results %>%
    mutate(obs_id = row_number())
  
  # Join predictions with evidence levels
  long_pred_with_evidence <- long_pred %>%
    left_join(
      sim_with_id %>% dplyr::select(obs_id, blue1, blue2),
      by = "obs_id"
    )
  
  # Summarize proportion of 1s per evidence combination
  pred_summary <- long_pred_with_evidence %>%
    group_by(blue1, blue2) %>%
    summarize(
      proportion = mean(choice, na.rm = TRUE), 
      n = n(),  
      se = sqrt((proportion * (1 - proportion)) / n),  # Binomial SE
      lower = proportion - 1.96 * se,  
      upper = proportion + 1.96 * se,  
      .groups = "drop"
    )

  # Generate title based on parameter name
  title <- ifelse(param_name == "prior_pred_choice", 
                  paste0("Prior Predictive Check for ", model_name),
                  paste0("Posterior Predictive Check for ", model_name))
  
  # Create plot
  ggplot(pred_summary, aes(x = blue1, y = proportion, color = factor(blue2), group = blue2)) +
    geom_line() +
    geom_point() +
    geom_ribbon(aes(ymin = lower, ymax = upper, fill = factor(blue2)), alpha = 0.2, color = NA) +
    ylim(0, 1) +
    labs(title = title,
         x = "Direct Evidence (Blue Marbles)",
         y = "Proportion of Choice = Blue",
         color = "Social Evidence",
         fill = "Social Evidence") +
    theme_minimal()
}

# Generate all plots
prior_simple_balanced <- plot_predictive_checks(fit_simple_balanced, simulation_results, "Simple Balanced", "prior_pred_choice")
prior_simple_self_focused <- plot_predictive_checks(fit_simple_self_focused, simulation_results, "Simple Self Focused", "prior_pred_choice")
prior_simple_socially_influenced <- plot_predictive_checks(fit_simple_socially_influenced, simulation_results, "Simple Socially Influenced", "prior_pred_choice")

#prior_weighted_balanced <- plot_predictive_checks(fit_weighted_balanced, simulation_results, "Weighted Balanced", "prior_pred_choice")
#prior_weighted_self_focused <- plot_predictive_checks(fit_weighted_self_focused, simulation_results, "Weighted Self Focused", "prior_pred_choice")
#prior_weighted_socially_influenced <- plot_predictive_checks(fit_weighted_socially_influenced, simulation_results, "Weighted Socially Influenced", "prior_pred_choice")

posterior_simple_balanced <- plot_predictive_checks(fit_simple_balanced, simulation_results, "Simple Balanced", "posterior_pred_choice")
posterior_simple_self_focused <- plot_predictive_checks(fit_simple_self_focused, simulation_results, "Simple Self Focused", "posterior_pred_choice")
posterior_simple_socially_influenced <- plot_predictive_checks(fit_simple_socially_influenced, simulation_results, "Simple Socially Influenced", "posterior_pred_choice")

posterior_weighted_balanced <- plot_predictive_checks(fit_weighted_balanced, simulation_results, "Weighted Balanced", "posterior_pred_choice")
posterior_weighted_self_focused <- plot_predictive_checks(fit_weighted_self_focused, simulation_results, "Weighted Self Focused", "posterior_pred_choice")
posterior_weighted_socially_influenced <- plot_predictive_checks(fit_weighted_socially_influenced, simulation_results, "Weighted Socially Influenced", "posterior_pred_choice")

# Arrange Prior Predictive Checks in a Grid
prior_grid <- (prior_simple_balanced + prior_simple_self_focused + prior_simple_socially_influenced) +#/  (prior_weighted_balanced + prior_weighted_self_focused + prior_weighted_socially_influenced) +
              plot_annotation(title = "Prior Predictive Checks")

# Arrange Posterior Predictive Checks in a Grid
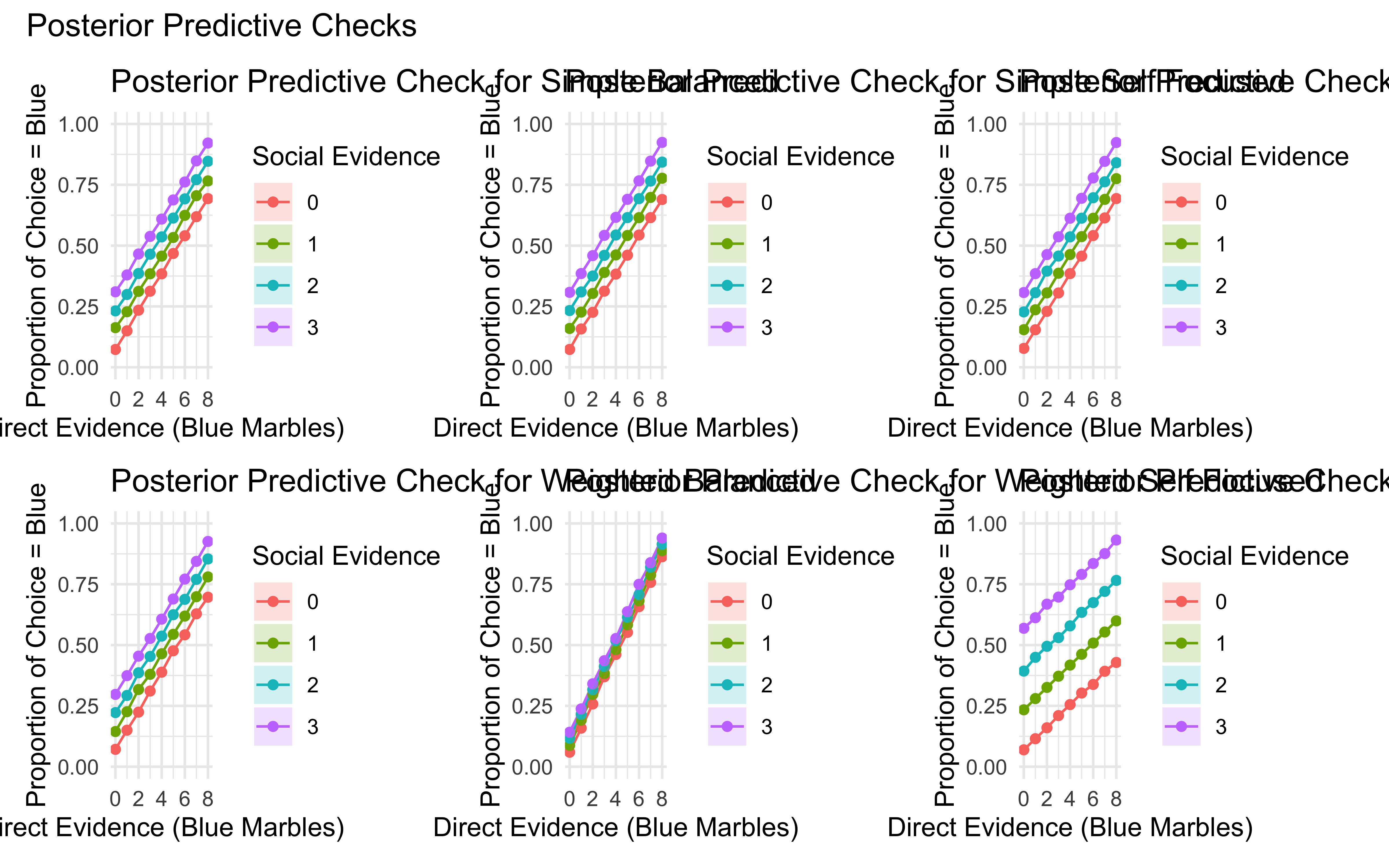
posterior_grid <- (posterior_simple_balanced + posterior_simple_self_focused + posterior_simple_socially_influenced) /
                  (posterior_weighted_balanced + posterior_weighted_self_focused + posterior_weighted_socially_influenced) +
                  plot_annotation(title = "Posterior Predictive Checks")

# Display the grids
print(prior_grid)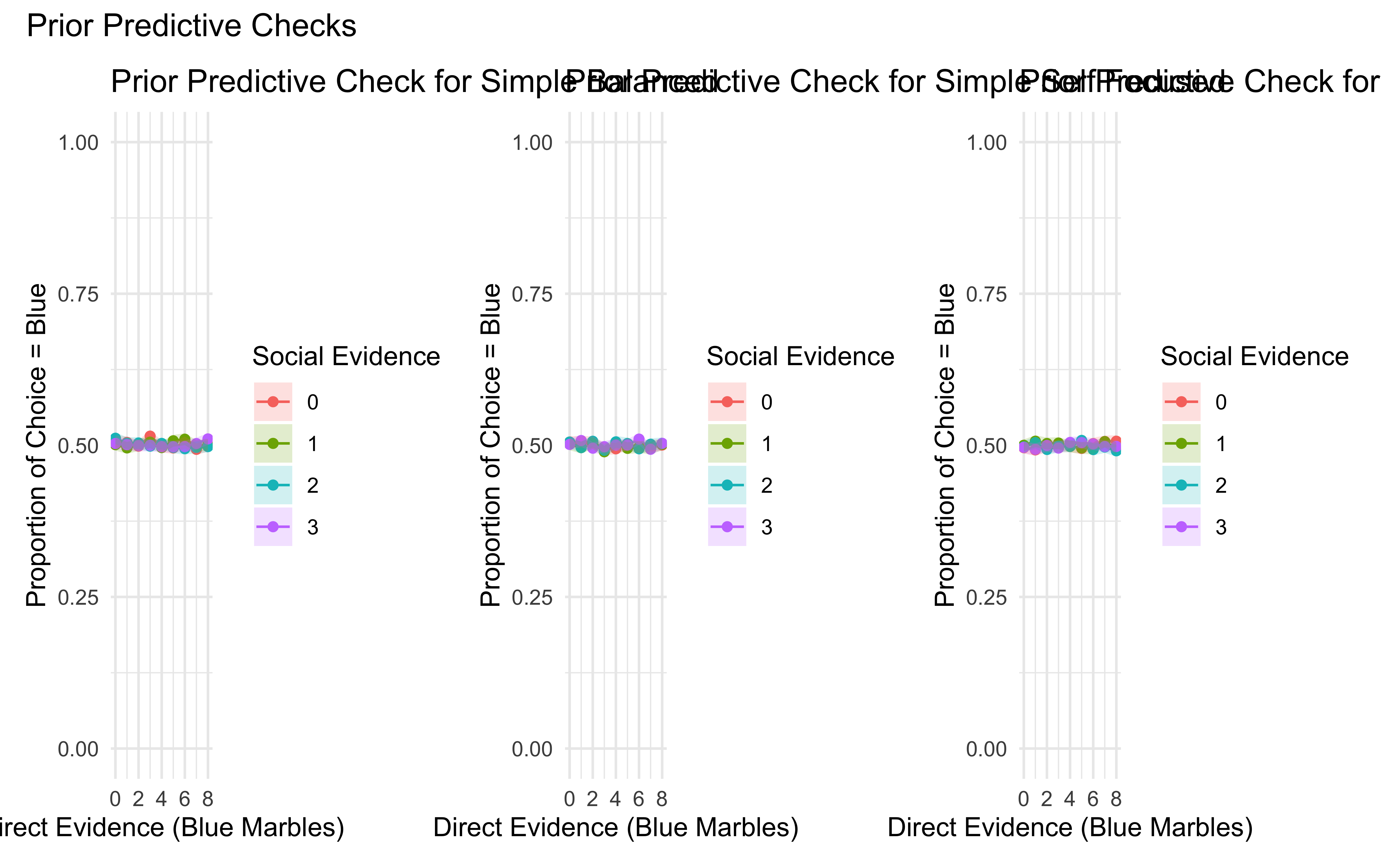

print(posterior_grid)

11.15 Prior-Posterior Update Visualization

This visualization shows how our beliefs change after observing data, comparing the prior and posterior distributions for key parameters.

# Function to plot prior-posterior updates for reparameterized model
plot_reparameterized_updates <- function(fit_list, true_params_list, model_names) {
  # Create dataframe for posterior values
  posterior_df <- tibble()
  
  # Process each model
  for (i in seq_along(fit_list)) {
    fit <- fit_list[[i]]
    model_name <- model_names[i]
    
    # Extract posterior draws
    draws_df <- as_draws_df(fit$draws())
    
    # Check which parameterization is used (old or new)
    if (all(c("total_weight", "weight_prop") %in% names(draws_df))) {
      # New parameterization - extract parameters directly
      temp_df <- tibble(
        model_name = model_name,
        parameter = "total_weight",
        value = draws_df$total_weight,
        distribution = "Posterior"
      )
      posterior_df <- bind_rows(posterior_df, temp_df)
      
      temp_df <- tibble(
        model_name = model_name,
        parameter = "weight_prop",
        value = draws_df$weight_prop,
        distribution = "Posterior"
      )
      posterior_df <- bind_rows(posterior_df, temp_df)
      
      # Also calculate the derived parameters for comparison with true values
      temp_df <- tibble(
        model_name = model_name,
        parameter = "weight_direct",
        value = draws_df$total_weight * draws_df$weight_prop,
        distribution = "Posterior (derived)"
      )
      posterior_df <- bind_rows(posterior_df, temp_df)
      
      temp_df <- tibble(
        model_name = model_name,
        parameter = "weight_social",
        value = draws_df$total_weight * (1 - draws_df$weight_prop),
        distribution = "Posterior (derived)"
      )
      posterior_df <- bind_rows(posterior_df, temp_df)
      
    } else if (all(c("weight_direct", "weight_social") %in% names(draws_df))) {
      # Old parameterization - extract and calculate equivalent new parameters
      temp_df <- tibble(
        model_name = model_name,
        parameter = "weight_direct",
        value = draws_df$weight_direct,
        distribution = "Posterior"
      )
      posterior_df <- bind_rows(posterior_df, temp_df)
      
      temp_df <- tibble(
        model_name = model_name,
        parameter = "weight_social",
        value = draws_df$weight_social,
        distribution = "Posterior"
      )
      posterior_df <- bind_rows(posterior_df, temp_df)
      
      # Calculate the equivalent new parameters
      total_weight <- draws_df$weight_direct + draws_df$weight_social
      weight_prop <- draws_df$weight_direct / total_weight
      
      temp_df <- tibble(
        model_name = model_name,
        parameter = "total_weight",
        value = total_weight,
        distribution = "Posterior (derived)"
      )
      posterior_df <- bind_rows(posterior_df, temp_df)
      
      temp_df <- tibble(
        model_name = model_name,
        parameter = "weight_prop",
        value = weight_prop,
        distribution = "Posterior (derived)"
      )
      posterior_df <- bind_rows(posterior_df, temp_df)
    } else {
      warning(paste("Unknown parameterization in model", model_name))
    }
  }
  
  # Generate prior samples based on recommended priors for new parameterization
  prior_df <- tibble()
  
  for (i in seq_along(model_names)) {
    model_name <- model_names[i]
    
    # Number of prior samples to match posterior
    n_samples <- 2000
    
    # Generate prior samples - gamma(2,1) for total_weight and beta(1,1) for weight_prop
    total_weight_prior <- rgamma(n_samples, shape = 2, rate = 1)
    weight_prop_prior <- rbeta(n_samples, 1, 1)
    
    # For the new parameterization
    temp_df <- tibble(
      model_name = model_name,
      parameter = "total_weight",
      value = total_weight_prior,
      distribution = "Prior"
    )
    prior_df <- bind_rows(prior_df, temp_df)
    
    temp_df <- tibble(
      model_name = model_name,
      parameter = "weight_prop",
      value = weight_prop_prior,
      distribution = "Prior"
    )
    prior_df <- bind_rows(prior_df, temp_df)
    
    # Calculate derived parameters for the old parameterization
    weight_direct_prior <- total_weight_prior * weight_prop_prior
    weight_social_prior <- total_weight_prior * (1 - weight_prop_prior)
    
    temp_df <- tibble(
      model_name = model_name,
      parameter = "weight_direct",
      value = weight_direct_prior,
      distribution = "Prior (derived)"
    )
    prior_df <- bind_rows(prior_df, temp_df)
    
    temp_df <- tibble(
      model_name = model_name,
      parameter = "weight_social",
      value = weight_social_prior,
      distribution = "Prior (derived)"
    )
    prior_df <- bind_rows(prior_df, temp_df)
  }
  
  # Combine prior and posterior
  combined_df <- bind_rows(prior_df, posterior_df)
  
  # Convert true parameter values
  true_values_df <- map2_dfr(true_params_list, model_names, function(params, model_name) {
    # Extract original parameters
    weight_direct <- params$weight_direct
    weight_social <- params$weight_social
    
    # Calculate new parameterization
    total_weight <- weight_direct + weight_social
    weight_prop <- weight_direct / total_weight
    
    tibble(
      model_name = model_name,
      parameter = c("weight_direct", "weight_social", "total_weight", "weight_prop"),
      value = c(weight_direct, weight_social, total_weight, weight_prop)
    )
  })
  
  # Create plots for different parameter sets
  
  # 1. New parameterization (total_weight and weight_prop)
  p1 <- combined_df %>% 
    filter(parameter %in% c("total_weight", "weight_prop")) %>%
    ggplot(aes(x = value, fill = distribution, color = distribution)) +
    geom_density(alpha = 0.3, linewidth = 1.2) +
    facet_grid(model_name ~ parameter, scales = "free") +
    scale_fill_manual(values = c("Prior" = "#E63946", 
                                "Prior (derived)" = "#E67946",
                                "Posterior" = "#1D3557", 
                                "Posterior (derived)" = "#1D5587")) +  
    scale_color_manual(values = c("Prior" = "#E63946", 
                                 "Prior (derived)" = "#E67946", 
                                 "Posterior" = "#1D3557", 
                                 "Posterior (derived)" = "#1D5587")) +
    geom_vline(data = true_values_df %>% filter(parameter %in% c("total_weight", "weight_prop")),
               aes(xintercept = value),
               color = "#2A9D8F", linetype = "dashed", linewidth = 1.2) +
    labs(title = "Prior vs. Posterior: New Parameterization",
         subtitle = "Green dashed lines indicate true parameter values",
         x = "Parameter Value",
         y = "Density",
         fill = "Distribution",
         color = "Distribution") +
    theme_minimal(base_size = 14) +
    theme(legend.position = "top")
  
  # 2. Original parameterization (weight_direct and weight_social)
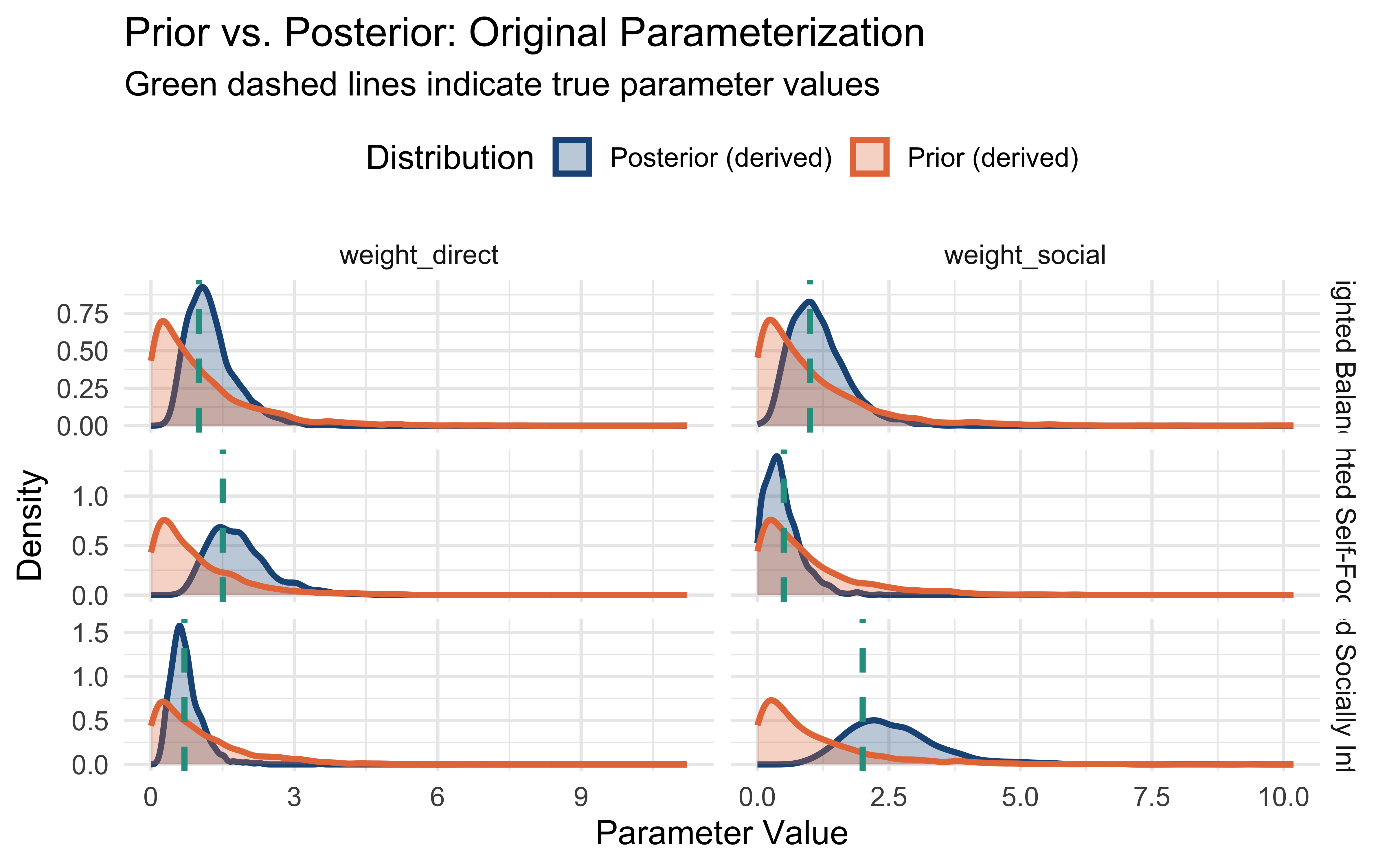
  p2 <- combined_df %>% 
    filter(parameter %in% c("weight_direct", "weight_social")) %>%
    ggplot(aes(x = value, fill = distribution, color = distribution)) +
    geom_density(alpha = 0.3, linewidth = 1.2) +
    facet_grid(model_name ~ parameter, scales = "free") +
    scale_fill_manual(values = c("Prior" = "#E63946", 
                                "Prior (derived)" = "#E67946",
                                "Posterior" = "#1D3557", 
                                "Posterior (derived)" = "#1D5587")) +  
    scale_color_manual(values = c("Prior" = "#E63946", 
                                 "Prior (derived)" = "#E67946", 
                                 "Posterior" = "#1D3557", 
                                 "Posterior (derived)" = "#1D5587")) +
    geom_vline(data = true_values_df %>% filter(parameter %in% c("weight_direct", "weight_social")),
               aes(xintercept = value),
               color = "#2A9D8F", linetype = "dashed", linewidth = 1.2) +
    labs(title = "Prior vs. Posterior: Original Parameterization",
         subtitle = "Green dashed lines indicate true parameter values",
         x = "Parameter Value",
         y = "Density",
         fill = "Distribution",
         color = "Distribution") +
    theme_minimal(base_size = 14) +
    theme(legend.position = "top")
  
  # Return both plots
  return(list(new_params = p1, old_params = p2))
}

fit_list <- list(
  fit_weighted_balanced,
  fit_weighted_self_focused,
  fit_weighted_socially_influenced
)

true_params_list <- list(
  list(weight_direct = 1, weight_social = 1),
  list(weight_direct = 1.5, weight_social = 0.5),
  list(weight_direct = 0.7, weight_social = 2)
)

model_names <- c("Weighted Balanced", "Weighted Self-Focused", "Weighted Socially Influenced")

# Generate the plots
plots <- plot_reparameterized_updates(fit_list, true_params_list, model_names)

# Display the plots
print(plots$new_params)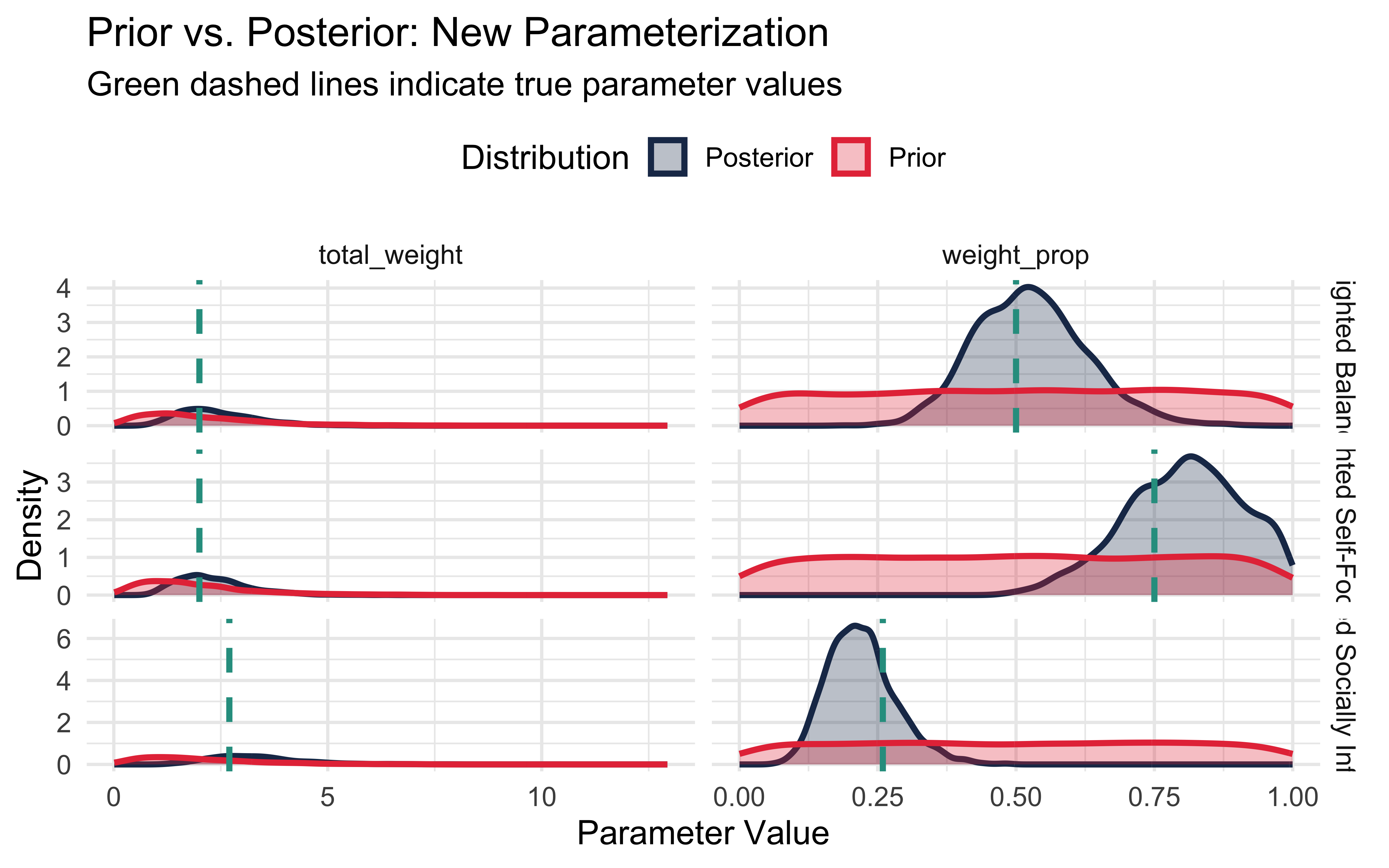

print(plots$old_params)

# Save the plots
ggsave("prior_posterior_new_params.pdf", plots$new_params, width = 12, height = 10)
ggsave("prior_posterior_old_params.pdf", plots$old_params, width = 12, height = 10)

11.16 Parameter recovery

## Parameter recovery
# Set random seed for reproducibility
set.seed(123)

## Set up parallel processing
future::plan(multisession, workers = parallel::detectCores() - 1)

# Define parameter grid for thorough testing
weight_values <- c(0, 0.2, 0.4, 0.6, 0.8, 1, 1.2, 1.4, 1.6, 1.8, 2)
n_trials <- c(1, 2, 3, 4, 5) # Number of times full combination of levels is repeated

# Create a grid of all parameter combinations to test
param_grid <- expand_grid(w1 = weight_values, w2 = weight_values, trials = n_trials)

# Define evidence combinations
evidence_combinations <- expand_grid(
  blue1 = 0:8,     # Direct evidence: number of blue marbles seen
  blue2 = 0:3,     # Social evidence: strength of blue evidence
  total1 = 8,      # Total marbles in direct evidence (constant)
  total2 = 3       # Total strength units in social evidence (constant)
)

# Function to generate decisions across all evidence combinations for a given agent
generate_agent_decisions <- function(weight_direct, weight_social, evidence_df, n_samples = 5) {
  # Create a data frame that repeats each evidence combination n_samples times
  repeated_evidence <- evidence_df %>%
    slice(rep(1:n(), each = n_samples)) %>%
    # Add a sample_id to distinguish between repetitions of the same combination
    group_by(blue1, blue2, total1, total2) %>%
    mutate(sample_id = 1:n()) %>%
    ungroup()
  
  # Apply our weighted Bayesian model to each evidence combination
  decisions <- pmap_dfr(repeated_evidence, function(blue1, blue2, total1, total2, sample_id) {
    # Calculate Bayesian integration with the agent's specific weights
    result <- weightedBetaBinomial(
      alpha_prior = 1, beta_prior = 1,
      blue1 = blue1, total1 = total1,
      blue2 = blue2, total2 = total2,
      weight_direct = weight_direct,
      weight_social = weight_social
    )
    
    # Return key decision metrics
    tibble(
      sample_id = sample_id,
      blue1 = blue1,
      blue2 = blue2,
      total1 = total1,
      total2 = total2,
      expected_rate = result$expected_rate,   # Probability the next marble is blue
      choice = result$decision,               # Final decision (Blue or Red)
      choice_binary = ifelse(result$decision == "Blue", 1, 0),
      confidence = result$confidence          # Confidence in decision
    )
  })
  
  return(decisions)
}

# Function to prepare Stan data
prepare_stan_data <- function(df) {
  list(
    N = nrow(df),
    choice = df$choice_binary,
    blue1 = df$blue1,
    total1 = df$total1,
    blue2 = df$blue2,
    total2 = df$total2
  )
}

# Compile the Stan model 
file_weighted <- file.path("stan/W10 _weighted_beta_binomial.stan")
mod_weighted <- cmdstan_model(file_weighted, cpp_options = list(stan_threads = TRUE))

# Function to fit model using cmdstanr
fit_model <- function(data) {
  stan_data <- prepare_stan_data(data)
  fit <- mod_weighted$sample(
    data = stan_data,
    seed = 126,
    chains = 2,
    parallel_chains = 2,
    threads_per_chain = 1,
    iter_warmup = 1000,
    iter_sampling = 1000,
    refresh = 0
  )
  return(fit)
}

# Run simulations and model fitting in parallel
results <- param_grid %>%
  mutate(
    # Generate synthetic data for each parameter combination
    data = future_pmap(list(w1, w2, trials), function(w1, w2, t) {
      generate_agent_decisions(w1, w2, evidence_combinations, t)
    }, .options = furrr_options(seed = TRUE)),
    
    # Fit model to each dataset
    fit = future_map(data, fit_model, .progress = TRUE)
  )

## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 1.2 seconds.
## Chain 2 finished in 1.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.2 seconds.
## Total execution time: 1.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.5 seconds.
## Chain 1 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 1.0 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.8 seconds.
## Chain 1 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 1.0 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 1.0 seconds.
## Chain 2 finished in 1.1 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.5 seconds.
## Chain 1 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.5 seconds.
## Chain 1 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.8 seconds.
## Chain 1 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.9 seconds.
## Chain 1 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.2 seconds.
## Chain 1 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 1.0 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.7 seconds.
## Chain 1 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.

## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.7 seconds.
## Chain 1 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 1.0 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.7 seconds.
## Chain 1 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 1.0 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.9 seconds.
## Chain 1 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.5 seconds.
## Chain 1 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.9 seconds.
## Chain 1 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.5 seconds.
## Chain 1 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.8 seconds.
## Chain 1 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.7 seconds.
## Chain 1 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.8 seconds.
## Chain 1 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.2 seconds.
## Chain 1 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.9 seconds.
## Chain 1 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.

## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.9 seconds.
## Chain 1 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 1.0 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.8 seconds.
## Chain 1 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.5 seconds.
## Chain 1 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.5 seconds.
## Chain 1 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 1.1 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 1.0 seconds.
## Chain 2 finished in 1.1 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.7 seconds.
## Chain 1 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.

## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.9 seconds.
## Chain 1 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.6 seconds.
## Chain 1 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.8 seconds.
## Chain 1 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.8 seconds.
## Chain 1 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.9 seconds.
## Chain 1 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.7 seconds.
## Chain 1 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.

## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.6 seconds.
## Chain 1 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.5 seconds.
## Chain 1 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.6 seconds.
## Chain 1 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.5 seconds.
## Chain 1 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.6 seconds.
## Chain 1 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.

## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.5 seconds.
## Chain 1 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.9 seconds.
## Chain 1 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.6 seconds.
## Chain 1 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.6 seconds.
## Chain 1 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 1.0 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.

## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.3 seconds.
## Chain 1 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.3 seconds.
## Chain 1 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.3 seconds.
## Chain 1 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 1.0 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.6 seconds.
## Chain 1 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.5 seconds.
## Chain 1 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.6 seconds.
## Chain 1 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.

## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.8 seconds.
## Chain 1 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.9 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.1 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 1.2 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.4 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.3 seconds.
## Chain 1 finished in 0.4 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.3 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.3 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 2 finished in 0.5 seconds.
## Chain 1 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.7 seconds.
## Chain 2 finished in 0.7 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.7 seconds.
## Total execution time: 0.8 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.9 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 1.0 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.4 seconds.
## Chain 2 finished in 0.3 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.4 seconds.
## Total execution time: 0.5 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.5 seconds.
## Chain 2 finished in 0.5 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.5 seconds.
## Total execution time: 0.6 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.7 seconds.
## 
## Running MCMC with 2 parallel chains, with 1 thread(s) per chain...
## 
## Chain 1 finished in 0.8 seconds.
## Chain 2 finished in 0.8 seconds.
## 
## Both chains finished successfully.
## Mean chain execution time: 0.8 seconds.
## Total execution time: 0.9 seconds.

# Extract both old and new parameterization results
results <- results %>%
  mutate(
    # First extract parameters in the new parameterization
    total_weight_est = map_dbl(fit, ~mean(as_draws_df(.x$draws())$total_weight)),
    weight_prop_est = map_dbl(fit, ~mean(as_draws_df(.x$draws())$weight_prop)),
    
    # Calculate the traditional parameters from the new parameterization
    weight_direct_est = total_weight_est * weight_prop_est,
    weight_social_est = total_weight_est * (1 - weight_prop_est),
    
    # Calculate the true parameters in the new parameterization 
    true_total_weight = w1 + w2,
    true_weight_prop = w1 / (w1 + w2),
    
    # Also extract uncertainty estimates
    total_weight_sd = map_dbl(fit, ~sd(as_draws_df(.x$draws())$total_weight)),
    weight_prop_sd = map_dbl(fit, ~sd(as_draws_df(.x$draws())$weight_prop)),
    weight_direct_sd = map_dbl(fit, function(x) {
      draws <- as_draws_df(x$draws())
      sd(draws$total_weight * draws$weight_prop)
    }),
    weight_social_sd = map_dbl(fit, function(x) {
      draws <- as_draws_df(x$draws())
      sd(draws$total_weight * (1 - draws$weight_prop))
    })
  )

# Create functions to visualize parameter recovery for both parameterizations
plot_recovery_original <- function(results_df) {
  # Visualize direct weight recovery
  p1 <- results_df %>%
    ggplot(aes(x = w1, y = weight_direct_est, color = factor(trials))) +
    geom_point() +
    geom_errorbar(aes(ymin = weight_direct_est - weight_direct_sd, 
                      ymax = weight_direct_est + weight_direct_sd), 
                  width = 0.1, alpha = 0.5) +
    geom_abline(slope = 1, intercept = 0, linetype = "dashed") +
    facet_wrap(~ w2, labeller = labeller(w2 = function(x) paste("Social Weight =", x))) +
    labs(title = "Direct Weight Parameter Recovery", 
         x = "True Direct Weight", 
         y = "Estimated Direct Weight",
         color = "Number of\nTrials per\nCondition") +
    theme_minimal() +
    theme(legend.position = "right")

  # Visualize social weight recovery
  p2 <- results_df %>%
    ggplot(aes(x = w2, y = weight_social_est, color = factor(trials))) +
    geom_point() +
    geom_errorbar(aes(ymin = weight_social_est - weight_social_sd, 
                      ymax = weight_social_est + weight_social_sd), 
                  width = 0.1, alpha = 0.5) +
    geom_abline(slope = 1, intercept = 0, linetype = "dashed") +
    facet_wrap(~ w1, labeller = labeller(w1 = function(x) paste("Direct Weight =", x))) +
    labs(title = "Social Weight Parameter Recovery", 
         x = "True Social Weight", 
         y = "Estimated Social Weight",
         color = "Number of\nTrials per\nCondition") +
    theme_minimal() +
    theme(legend.position = "right")
    
  return(list(direct = p1, social = p2))
}

plot_recovery_new <- function(results_df) {
  # Visualize total weight recovery
  # First, create discrete categories for weight proportion to avoid using continuous variable in facet_wrap
  results_with_categories <- results_df %>%
    filter(true_total_weight > 0) %>% # Avoid division by zero issues
    mutate(weight_prop_cat = cut(true_weight_prop, 
                               breaks = c(0, 0.25, 0.5, 0.75, 1.0),
                               labels = c("0-0.25", "0.25-0.5", "0.5-0.75", "0.75-1.0"),
                               include.lowest = TRUE))
  
  p1 <- results_with_categories %>%
    ggplot(aes(x = true_total_weight, y = total_weight_est, color = factor(trials))) +
    geom_point() +
    geom_errorbar(aes(ymin = total_weight_est - total_weight_sd, 
                      ymax = total_weight_est + total_weight_sd), 
                  width = 0.1, alpha = 0.5) +
    geom_abline(slope = 1, intercept = 0, linetype = "dashed") +
    facet_wrap(~ weight_prop_cat, labeller = labeller(
      weight_prop_cat = function(x) paste("Weight Proportion =", x)
    )) +
    labs(title = "Total Weight Parameter Recovery", 
         x = "True Total Weight", 
         y = "Estimated Total Weight",
         color = "Number of\nTrials per\nCondition") +
    theme_minimal() +
    theme(legend.position = "right")

  # Visualize weight proportion recovery
  # Create discrete categories for total weight
  results_with_categories <- results_df %>%
    filter(true_total_weight > 0) %>% # Avoid division by zero issues
    mutate(total_weight_cat = cut(true_total_weight, 
                                breaks = c(0, 0.5, 1.0, 1.5, 2.0),
                                labels = c("0-0.5", "0.5-1.0", "1.0-1.5", "1.5-2.0"),
                                include.lowest = TRUE))
  
  p2 <- results_with_categories %>%
    ggplot(aes(x = true_weight_prop, y = weight_prop_est, color = factor(trials))) +
    geom_point() +
    geom_errorbar(aes(ymin = weight_prop_est - weight_prop_sd, 
                      ymax = weight_prop_est + weight_prop_sd), 
                  width = 0.01, alpha = 0.5) +
    geom_abline(slope = 1, intercept = 0, linetype = "dashed") +
    facet_wrap(~ total_weight_cat, labeller = labeller(
      total_weight_cat = function(x) paste("Total Weight =", x)
    )) +
    labs(title = "Weight Proportion Parameter Recovery", 
         x = "True Weight Proportion", 
         y = "Estimated Weight Proportion",
         color = "Number of\nTrials per\nCondition") +
    theme_minimal() +
    theme(legend.position = "right")
    
  return(list(total = p1, prop = p2))
}

# Generate plots
original_recovery_plots <- plot_recovery_original(results)
new_recovery_plots <- plot_recovery_new(results)

# Display plots for new parameterization
new_recovery_plots$total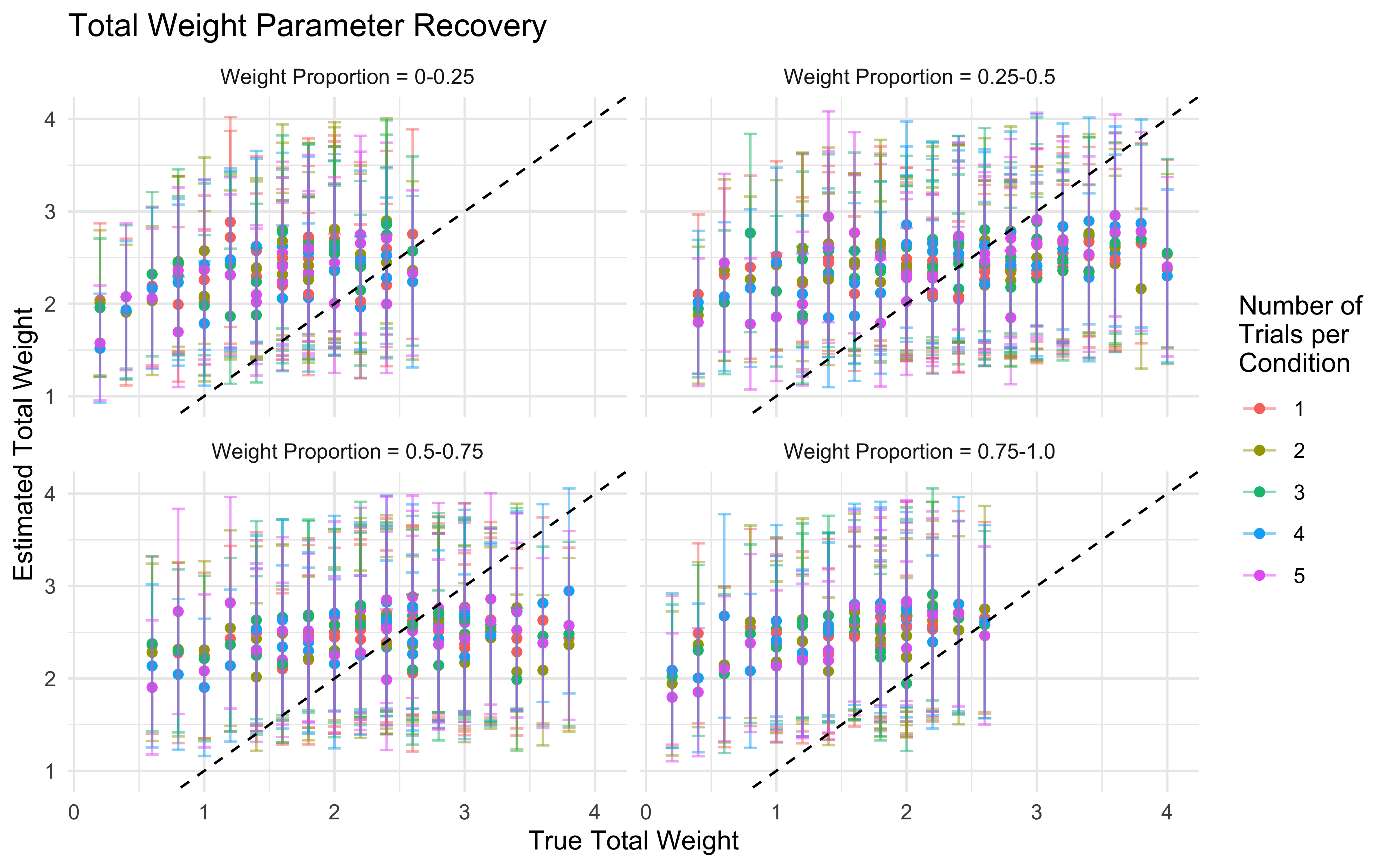

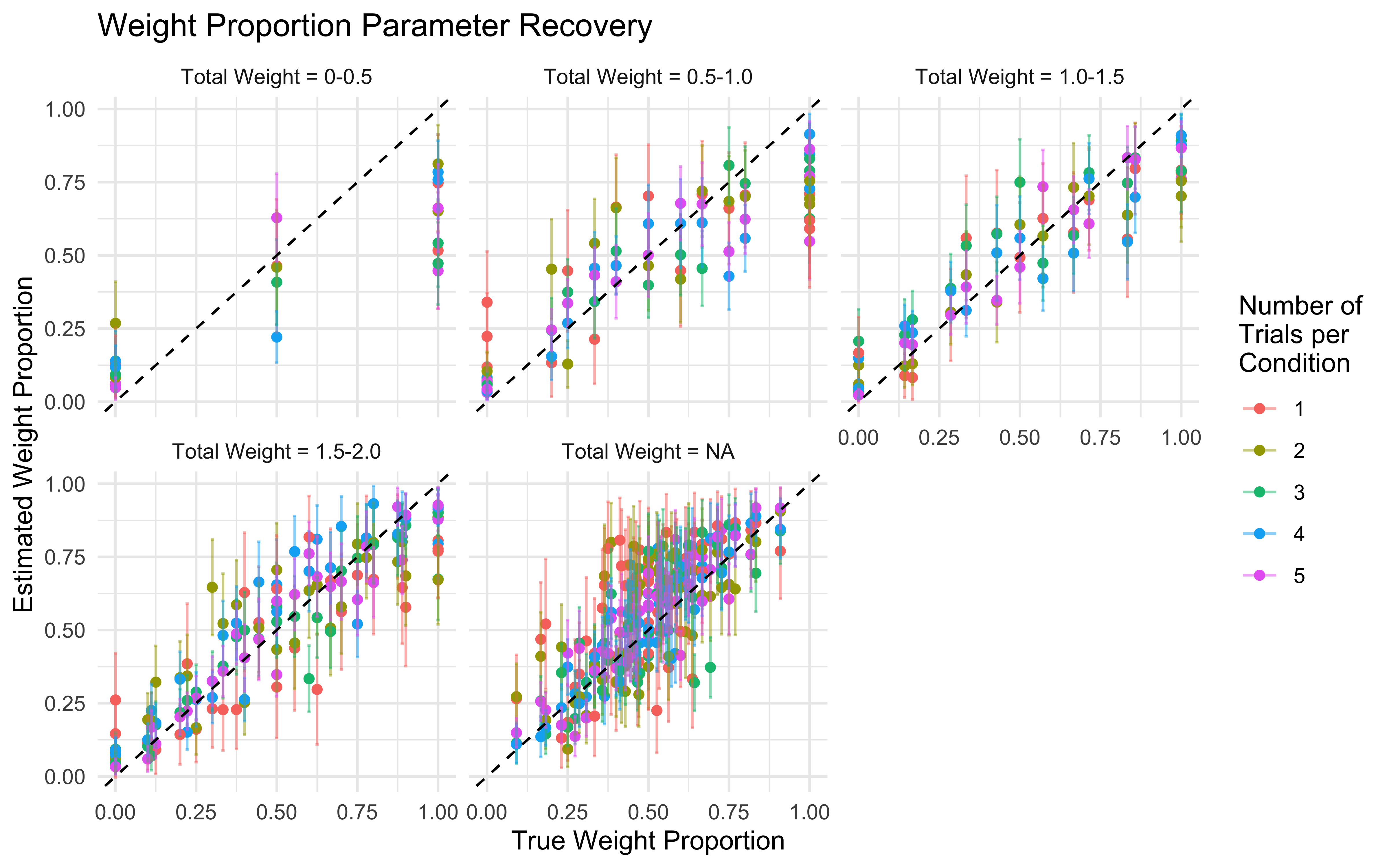
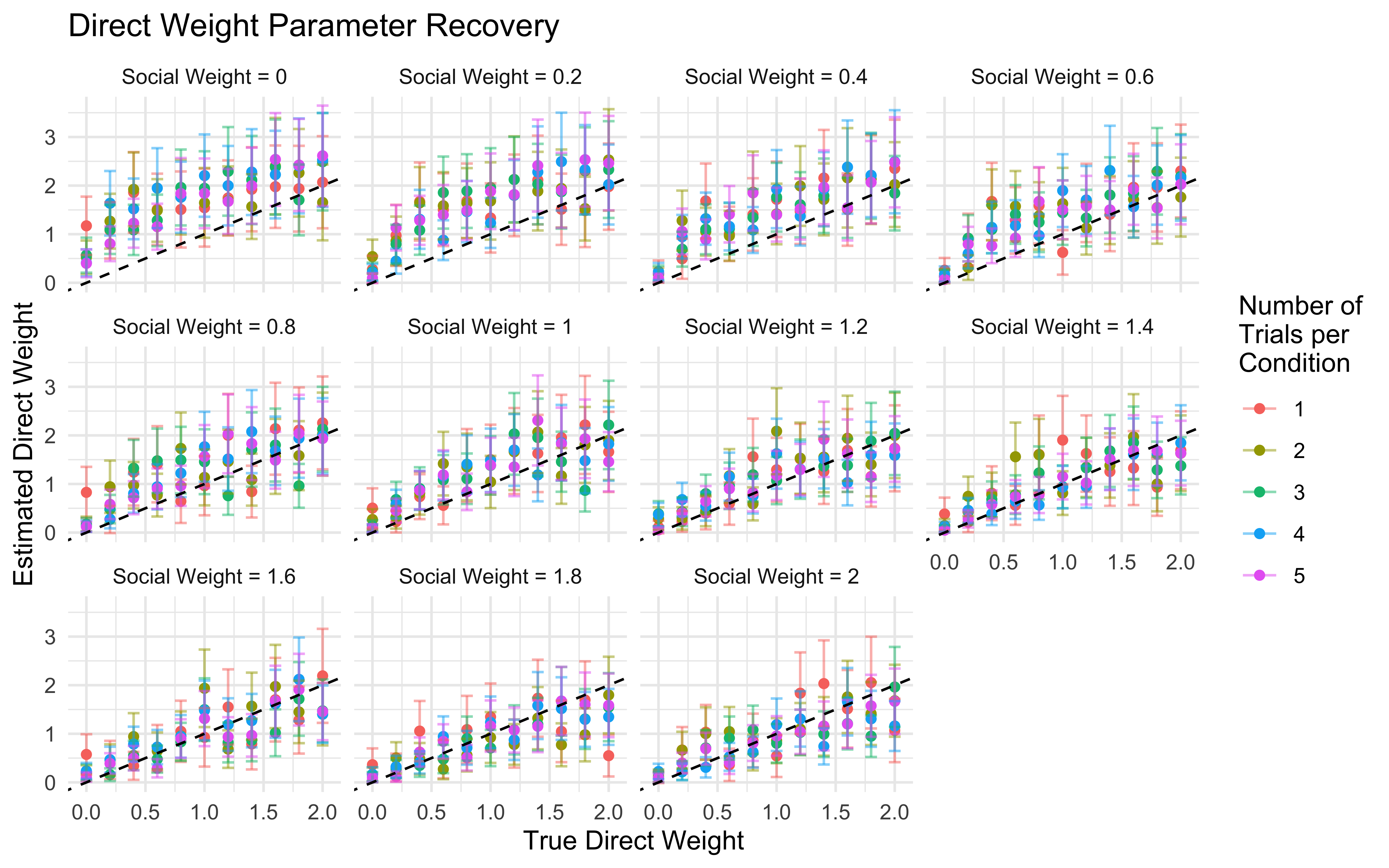
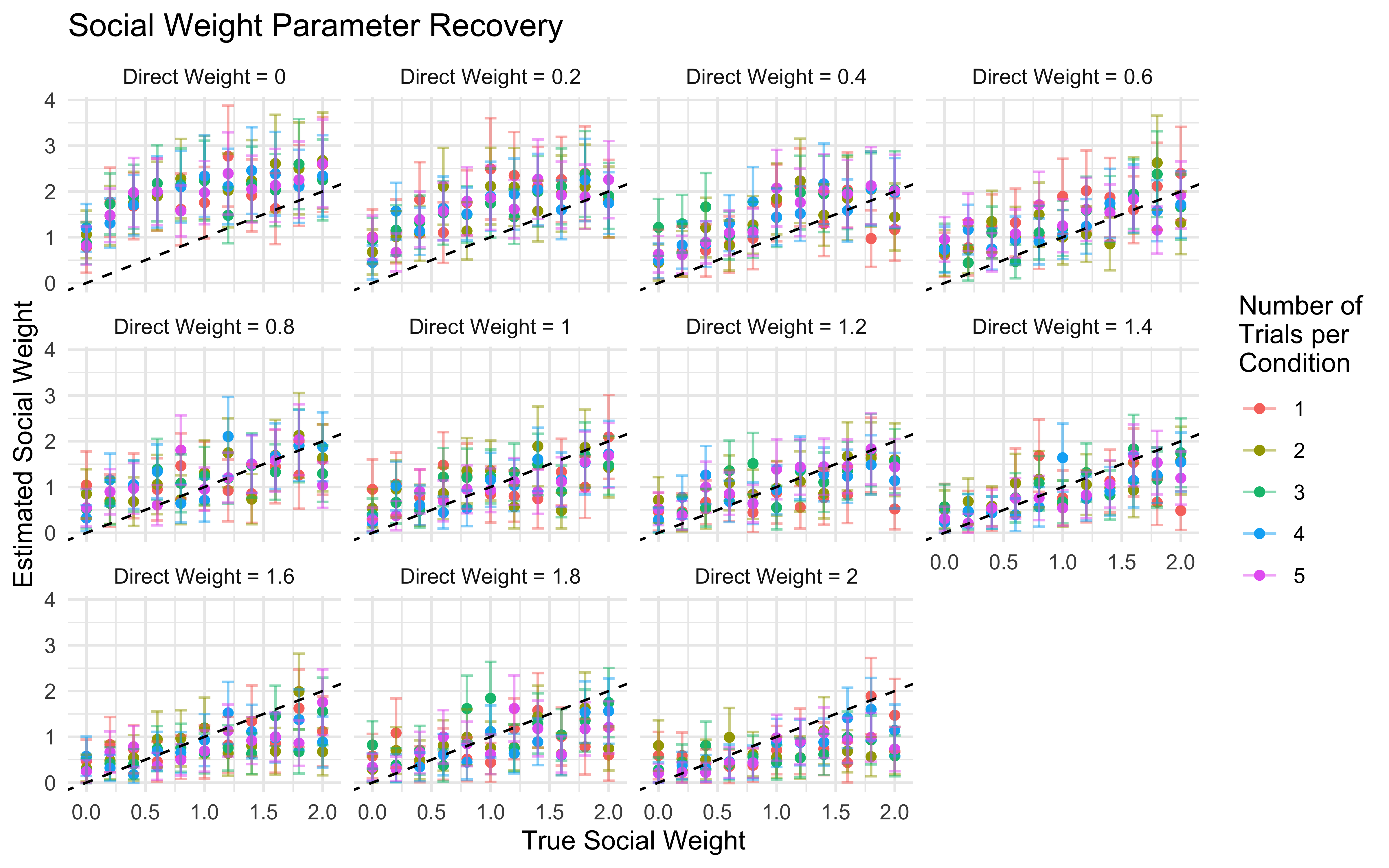
new_recovery_plots$prop

# Display plots for original parameterization
original_recovery_plots$direct

original_recovery_plots$social

# Analysis of recovery quality by parameter combination
recovery_summary <- results %>%
  mutate(
    # Calculate error metrics for original parameterization
    error_direct = abs(weight_direct_est - w1),
    error_social = abs(weight_social_est - w2),
    rel_error_direct = ifelse(w1 > 0, error_direct / w1, NA),
    rel_error_social = ifelse(w2 > 0, error_social / w2, NA),
    
    # Calculate error metrics for new parameterization
    error_total = abs(total_weight_est - true_total_weight),
    error_prop = abs(weight_prop_est - true_weight_prop),
    rel_error_total = ifelse(true_total_weight > 0, error_total / true_total_weight, NA),
    rel_error_prop = ifelse(true_weight_prop > 0, error_prop / true_weight_prop, NA)
  ) %>%
  group_by(trials) %>%
  summarize(
    mean_error_direct = mean(error_direct, na.rm = TRUE),
    mean_error_social = mean(error_social, na.rm = TRUE),
    mean_rel_error_direct = mean(rel_error_direct, na.rm = TRUE),
    mean_rel_error_social = mean(rel_error_social, na.rm = TRUE),
    mean_error_total = mean(error_total, na.rm = TRUE),
    mean_error_prop = mean(error_prop, na.rm = TRUE),
    mean_rel_error_total = mean(rel_error_total, na.rm = TRUE),
    mean_rel_error_prop = mean(rel_error_prop, na.rm = TRUE),
    .groups = "drop"
  )

# Display summary table
knitr::kable(recovery_summary, 
             digits = 3,
             caption = "Parameter Recovery Quality by Number of Trials")

Table 11.1: Parameter Recovery Quality by Number of Trials
trials	mean_error_direct	mean_error_social	mean_rel_error_direct	mean_rel_error_social	mean_error_total	mean_error_prop	mean_rel_error_total	mean_rel_error_prop
1	0.436	0.560	0.652	0.833	0.784	0.151	0.774	0.339
2	0.431	0.524	0.742	0.742	0.795	0.126	0.768	0.315
3	0.404	0.487	0.627	0.740	0.780	0.102	0.764	0.211
4	0.389	0.442	0.611	0.736	0.740	0.097	0.719	0.208
5	0.350	0.451	0.569	0.666	0.721	0.087	0.690	0.184

# Create a summary visualization showing how recovery improves with more trials
p_summary <- recovery_summary %>%
  pivot_longer(
    cols = starts_with("mean_"),
    names_to = "metric",
    values_to = "value"
  ) %>%
  mutate(
    parameter_type = case_when(
      grepl("direct", metric) ~ "Direct Weight",
      grepl("social", metric) ~ "Social Weight",
      grepl("total", metric) ~ "Total Weight",
      grepl("prop", metric) ~ "Weight Proportion"
    ),
    error_type = case_when(
      grepl("rel_error", metric) ~ "Relative Error",
      TRUE ~ "Absolute Error"
    )
  ) %>%
  ggplot(aes(x = trials, y = value, color = parameter_type, linetype = error_type)) +
  geom_line(size = 1) +
  geom_point(size = 3) +
  facet_wrap(~ error_type, scales = "free_y") +
  labs(
    title = "Parameter Recovery Improvement with Increased Trials",
    x = "Number of Trials per Evidence Combination",
    y = "Mean Error",
    color = "Parameter",
    linetype = "Error Type"
  ) +
  theme_minimal()

p_summary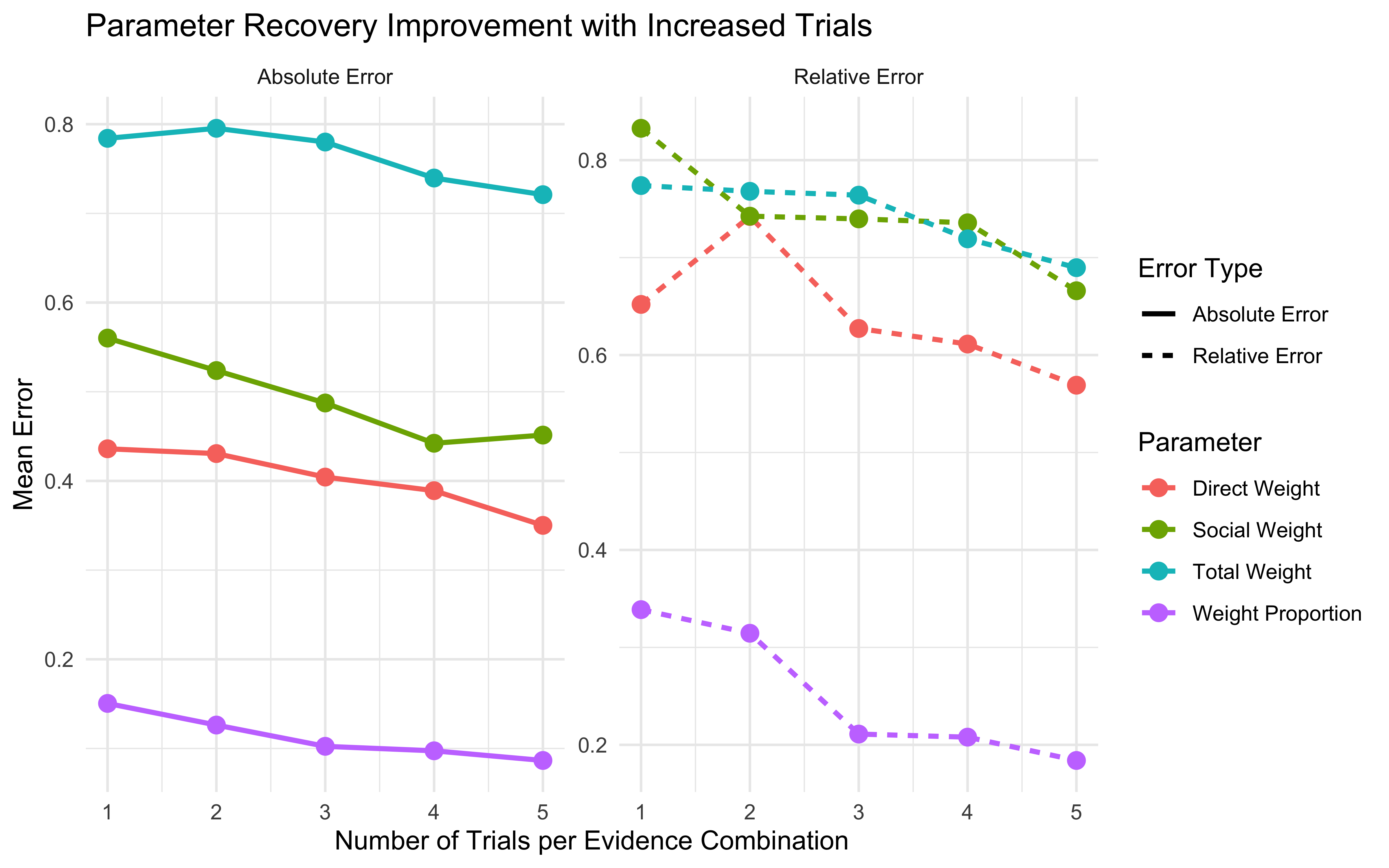

11.17 Model comparison

11.18 Leave-One-Out Cross-Validation and Model Comparison

In this section, we’ll explore how to compare the simple Bayesian agent (where weights are equal) and the weighted Bayesian agent (where weights can differ) using Leave-One-Out Cross-Validation (LOO-CV). We’ll leverage the models we’ve already fitted to our three simulated agent types: Balanced, Self-Focused, and Socially-Influenced.

11.18.1 Understanding LOO Cross-Validation in Bayesian Framework

LOO-CV is a powerful method for model comparison that estimates how well a model will predict new, unseen data. At its core, LOO-CV works by:

Leaving out one observation at a time
Fitting the model on all remaining observations
Predicting the left-out observation using that model
Repeating for all observations and aggregating the results

In a Bayesian context, exact LOO-CV would require refitting our model N times (where N is the number of observations), which is computationally expensive. Instead, we use Pareto-Smoothed Importance Sampling (PSIS-LOO), which approximates LOO-CV from a single model fit.

The key insight of PSIS-LOO is that we can use importance sampling to approximate how the posterior would change if an observation were removed:

\[p(\theta | y_{-i}) \approx \frac{p(\theta | y)}{p(y_i | \theta)} \propto \frac{p(\theta | y)}{p(y_i | \theta)}\]

where \(p(\theta | y_{-i})\) is the posterior without observation \(i\), and \(p(\theta | y)\) is the full posterior.

11.18.2 Step-by-Step Implementation of LOO-CV

Let’s apply LOO-CV to compare our models across the three scenarios.

# Load the loo package
library(loo)

# Function to extract log-likelihood and compute LOO
compute_loo <- function(model_fit) {
  # Extract log-likelihood values
  log_lik <- model_fit$draws("log_lik", format = "matrix")
  
  # Compute LOO-CV using PSIS
  loo_result <- loo(log_lik)
  return(loo_result)
}

# Compute LOO for each model and scenario
loo_simple_balanced <- compute_loo(fit_simple_balanced)
loo_simple_self_focused <- compute_loo(fit_simple_self_focused)
loo_simple_socially_influenced <- compute_loo(fit_simple_socially_influenced)

loo_weighted_balanced <- compute_loo(fit_weighted_balanced)
loo_weighted_self_focused <- compute_loo(fit_weighted_self_focused)
loo_weighted_socially_influenced <- compute_loo(fit_weighted_socially_influenced)

11.18.3 Understanding PSIS-LOO Diagnostics

Before we compare models, it’s important to check the reliability of our LOO estimates. PSIS-LOO provides diagnostics through the Pareto k values:

# Function to check Pareto k diagnostics
check_pareto_k <- function(loo_result, model_name) {
  # Extract Pareto k values
  pareto_k <- loo_result$diagnostics$pareto_k
  
  # Count problematic k values
  n_k_high <- sum(pareto_k > 0.7)
  n_k_medium <- sum(pareto_k > 0.5 & pareto_k <= 0.7)
  
  # Proportion of problematic observations
  prop_problematic <- (n_k_high + n_k_medium) / length(pareto_k)
  
  # Create diagnostic summary
  summary_df <- tibble(
    model = model_name,
    total_obs = length(pareto_k),
    k_high = n_k_high,
    k_medium = n_k_medium,
    prop_problematic = prop_problematic,
    reliability = case_when(
      prop_problematic == 0 ~ "Excellent",
      prop_problematic < 0.05 ~ "Good",
      prop_problematic < 0.1 ~ "Fair",
      TRUE ~ "Poor"
    )
  )
  
  return(summary_df)
}

# Check diagnostics for all models
diagnostics <- bind_rows(
  check_pareto_k(loo_simple_balanced, "Simple - Balanced"),
  check_pareto_k(loo_simple_self_focused, "Simple - Self-Focused"),
  check_pareto_k(loo_simple_socially_influenced, "Simple - Socially-Influenced"),
  check_pareto_k(loo_weighted_balanced, "Weighted - Balanced"),
  check_pareto_k(loo_weighted_self_focused, "Weighted - Self-Focused"),
  check_pareto_k(loo_weighted_socially_influenced, "Weighted - Socially-Influenced")
)

# Display diagnostics table
knitr::kable(diagnostics, 
             digits = 3,
             caption = "PSIS-LOO Reliability Diagnostics")

Table 11.2: PSIS-LOO Reliability Diagnostics
model	total_obs	k_high	prop_problematic	reliability
Simple - Balanced	180	180	1	Poor
Simple - Self-Focused	180	180	1	Poor
Simple - Socially-Influenced	180	180	1	Poor
Weighted - Balanced	180	0	0	Excellent
Weighted - Self-Focused	180	0	0	Excellent
Weighted - Socially-Influenced	180	0	0	Excellent

11.18.4 Model Comparison for Each Scenario

Now we can compare the models within each scenario:

# Function to compare models and create visualization
compare_scenario_models <- function(loo_simple, loo_weighted, scenario_name) {
  # Compare models
  comparison <- loo_compare(loo_simple, loo_weighted)
  
  # Calculate model weights
  weights <- loo_model_weights(list(
    "Simple Bayesian" = loo_simple,
    "Weighted Bayesian" = loo_weighted
  ))
  
  # Print comparison
  cat("\nModel comparison for", scenario_name, "scenario:\n")
  print(comparison)
  
  # Print weights
  cat("\nModel weights for", scenario_name, "scenario:\n")
  print(weights)
  
  # Create comparison dataframe
  comparison_df <- as.data.frame(comparison)
  comparison_df$model <- rownames(comparison_df)
  rownames(comparison_df) <- NULL
  comparison_df$scenario <- scenario_name
  
  # Create weights dataframe
  weights_df <- tibble(
    model = names(weights),
    weight = as.numeric(weights),
    scenario = scenario_name
  )
  
  # Return both dataframes
  return(list(comparison = comparison_df, weights = weights_df))
}

# Perform comparisons for each scenario
balanced_comparison <- compare_scenario_models(
  loo_simple_balanced, loo_weighted_balanced, "Balanced"
)

## 
## Model comparison for Balanced scenario:
##        elpd_diff se_diff
## model1  0.0       0.0   
## model2 -1.0       0.3   
## 
## Model weights for Balanced scenario:
## Method: stacking
## ------
##                   weight
## Simple Bayesian   1.000 
## Weighted Bayesian 0.000

self_focused_comparison <- compare_scenario_models(
  loo_simple_self_focused, loo_weighted_self_focused, "Self-Focused"
)

## 
## Model comparison for Self-Focused scenario:
##        elpd_diff se_diff
## model2  0.0       0.0   
## model1 -3.1       2.6   
## 
## Model weights for Self-Focused scenario:
## Method: stacking
## ------
##                   weight
## Simple Bayesian   0.085 
## Weighted Bayesian 0.915

socially_influenced_comparison <- compare_scenario_models(
  loo_simple_socially_influenced, loo_weighted_socially_influenced, "Socially-Influenced"
)

## 
## Model comparison for Socially-Influenced scenario:
##        elpd_diff se_diff
## model2  0.0       0.0   
## model1 -6.2       3.5   
## 
## Model weights for Socially-Influenced scenario:
## Method: stacking
## ------
##                   weight
## Simple Bayesian   0.000 
## Weighted Bayesian 1.000

# Combine comparison results
all_comparisons <- bind_rows(
  balanced_comparison$comparison,
  self_focused_comparison$comparison,
  socially_influenced_comparison$comparison
)

all_weights <- bind_rows(
  balanced_comparison$weights,
  self_focused_comparison$weights,
  socially_influenced_comparison$weights
)

11.18.5 Visualizing the Comparison Results

Let’s create informative visualizations to better understand the comparison results:

# Plot ELPD differences
p1 <- ggplot(all_comparisons, 
             aes(x = model, y = elpd_diff, fill = model)) +
  geom_col() +
  geom_errorbar(aes(ymin = elpd_diff - se_diff, 
                    ymax = elpd_diff + se_diff), 
                width = 0.2) +
  facet_wrap(~ scenario, scales = "free_y") +
  labs(
    title = "Model Comparison via LOO-CV",
    subtitle = "Higher ELPD difference is better; error bars show ±1 SE",
    x = NULL,
    y = "ELPD Difference"
  ) +
  scale_fill_brewer(palette = "Set1") +
  theme_minimal() +
  theme(legend.position = "bottom")

# Plot model weights
p2 <- ggplot(all_weights, 
             aes(x = model, y = weight, fill = model)) +
  geom_col() +
  geom_text(aes(label = scales::percent(weight, accuracy = 0.1)), 
            vjust = -0.5, size = 4) +
  facet_wrap(~ scenario) +
  labs(
    title = "Model Weights Based on LOO-CV",
    subtitle = "Higher weights indicate better predictive performance",
    x = NULL,
    y = "Model Weight"
  ) +
  scale_fill_brewer(palette = "Set1") +
  theme_minimal() +
  theme(legend.position = "bottom") +
  ylim(0, 1)

# Display plots
p1 + p2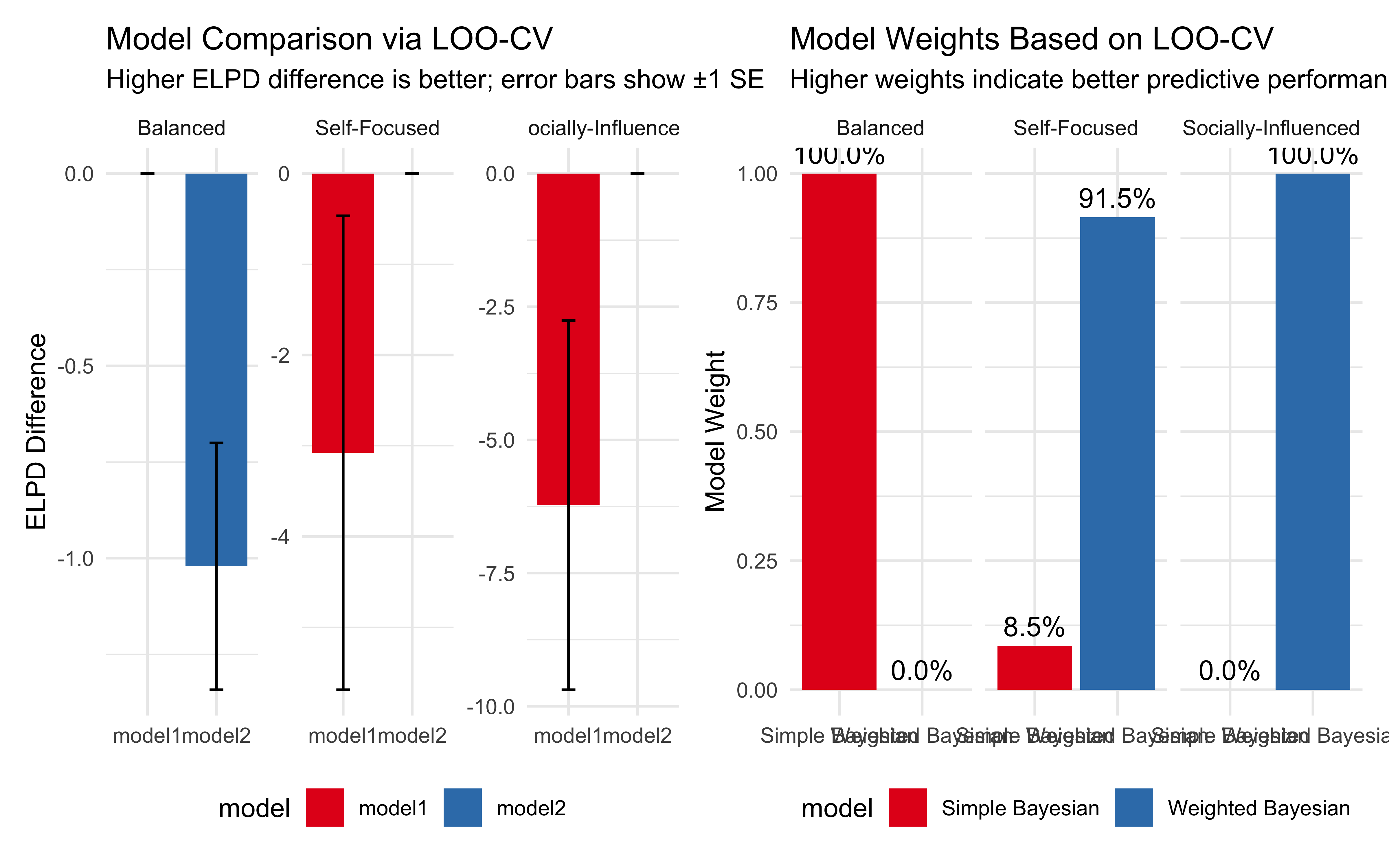

# Create a summary table of results
summary_table <- all_weights %>%
  pivot_wider(names_from = model, values_from = weight) %>%
  mutate(
    winning_model = case_when(
      `Simple Bayesian` > `Weighted Bayesian` ~ "Simple Bayesian",
      `Weighted Bayesian` > `Simple Bayesian` ~ "Weighted Bayesian",
      TRUE ~ "Tie"
    ),
    weight_difference = abs(`Simple Bayesian` - `Weighted Bayesian`),
    evidence_strength = case_when(
      weight_difference < 0.1 ~ "Weak",
      weight_difference < 0.3 ~ "Moderate",
      weight_difference < 0.6 ~ "Strong",
      TRUE ~ "Very Strong"
    )
  )

# Display summary table
knitr::kable(summary_table, 
             digits = 3,
             caption = "Summary of Model Comparison Results")

Table 11.3: Summary of Model Comparison Results
scenario	Simple Bayesian	Weighted Bayesian	winning_model	weight_difference	evidence_strength
Balanced	1.000	0.000	Simple Bayesian	1.00	Very Strong
Self-Focused	0.085	0.915	Weighted Bayesian	0.83	Very Strong
Socially-Influenced	0.000	1.000	Weighted Bayesian	1.00	Very Strong

11.18.6 Understanding the Results

Now let’s take a deeper look at what these LOO comparisons tell us:

11.18.6.1 1. Balanced Agent Scenario

In the Balanced Agent scenario (where both direct and social evidence are weighted equally), we expect the simple Bayesian model to perform well, since it assumes equal weights by design. If our LOO comparison shows the weighted model doesn’t provide much advantage, this confirms our expectations - the additional complexity of differential weighting isn’t justified when the true process gives equal weight to evidence sources.

11.18.6.2 2. Self-Focused Agent Scenario

For the Self-Focused Agent (who overweights direct evidence and underweights social evidence), we expect the weighted Bayesian model to outperform the simple model. If the LOO comparison shows a substantial advantage for the weighted model, it suggests that capturing the differential weighting of evidence is important for predicting this agent’s behavior.

11.18.6.3 3. Socially-Influenced Agent Scenario

Similarly, for the Socially-Influenced Agent (who overweights social evidence), we expect the weighted model to have an advantage. The size of this advantage indicates how crucial it is to account for the specific weighting pattern to understand this agent’s decision-making process.

11.18.7 The Mathematics Behind LOO-CV

Let’s look at the mathematical foundations of LOO-CV to better understand what’s happening:

Log Predictive Density: For each observation \(i\), the log predictive density is:

\[\log p(y_i | y_{-i}) = \log \int p(y_i | \theta) p(\theta | y_{-i}) d\theta\]

This represents how well we can predict observation \(i\) using a model trained on all other observations.
PSIS-LOO Approximation: Since we don’t want to refit our model for each observation, we use importance sampling:

\[\log p(y_i | y_{-i}) \approx \log \frac{\sum_{j=1}^S w_i^j p(y_i | \theta^j)}{\sum_{j=1}^S w_i^j}\]

where \(w_i^j \propto \frac{1}{p(y_i | \theta^j)}\) are importance weights and \(\theta^j\) are samples from the full posterior.
Expected Log Predictive Density (ELPD): The overall measure of model predictive accuracy is:

\[\text{ELPD} = \sum_{i=1}^N \log p(y_i | y_{-i})\]

Higher ELPD values indicate better predictive performance.

11.18.8 Examining Pointwise Contributions to LOO

To understand where model differences arise, we can look at the pointwise contributions to LOO:

# Extract pointwise values
pointwise_balanced <- tibble(
  observation = 1:length(loo_simple_balanced$pointwise[,"elpd_loo"]),
  simple = loo_simple_balanced$pointwise[,"elpd_loo"],
  weighted = loo_weighted_balanced$pointwise[,"elpd_loo"],
  difference = weighted - simple,
  scenario = "Balanced"
)

pointwise_self_focused <- tibble(
  observation = 1:length(loo_simple_self_focused$pointwise[,"elpd_loo"]),
  simple = loo_simple_self_focused$pointwise[,"elpd_loo"],
  weighted = loo_weighted_self_focused$pointwise[,"elpd_loo"],
  difference = weighted - simple,
  scenario = "Self-Focused"
)

pointwise_socially_influenced <- tibble(
  observation = 1:length(loo_simple_socially_influenced$pointwise[,"elpd_loo"]),
  simple = loo_simple_socially_influenced$pointwise[,"elpd_loo"],
  weighted = loo_weighted_socially_influenced$pointwise[,"elpd_loo"],
  difference = weighted - simple,
  scenario = "Socially-Influenced"
)

# Combine pointwise data
all_pointwise <- bind_rows(
  pointwise_balanced,
  pointwise_self_focused,
  pointwise_socially_influenced
)

# Plot pointwise differences
ggplot(all_pointwise, aes(x = observation, y = difference)) +
  geom_col(aes(fill = difference > 0)) +
  geom_hline(yintercept = 0, linetype = "dashed") +
  facet_wrap(~ scenario, scales = "free_x") +
  scale_fill_manual(values = c("TRUE" = "green4", "FALSE" = "firebrick"),
                   name = "Weighted Better?") +
  labs(
    title = "Pointwise Differences in ELPD Between Models",
    subtitle = "Green bars indicate observations where the weighted model performs better",
    x = "Observation",
    y = "ELPD Difference (Weighted - Simple)"
  ) +
  theme_minimal() +
  theme(legend.position = "bottom")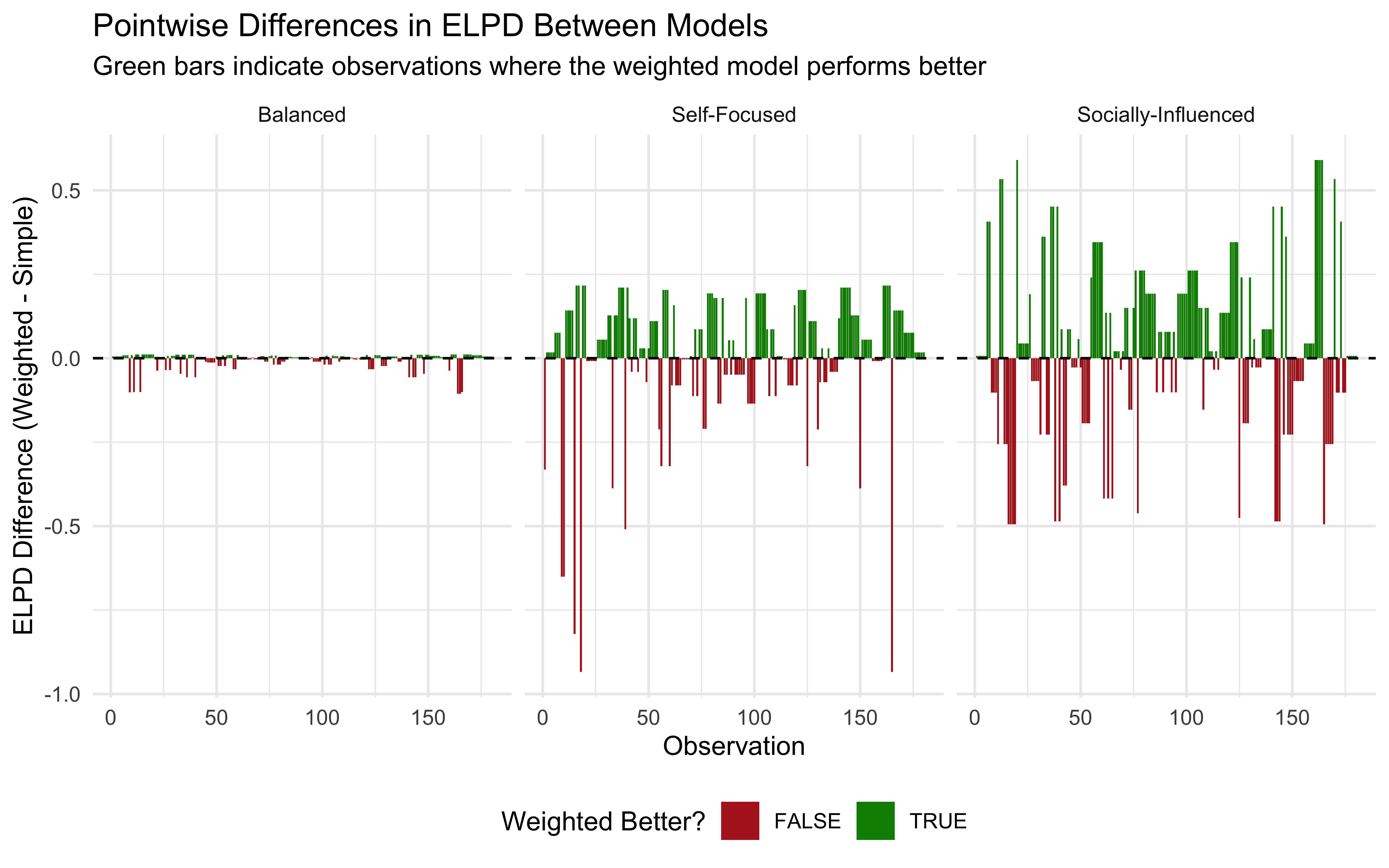

11.19 Multilevel Bayesian Models

In the previous sections, we explored how individuals integrate direct and social evidence using Bayesian principles. However, our models assumed that all individuals use the same weighting strategy. In reality, people vary in how they weigh different sources of information - some may trust their own observations more, while others may be more influenced by social information.

Multilevel (hierarchical) models allow us to capture this individual variation while still leveraging the commonalities across individuals. They offer several advantages:

They model individual differences explicitly
They improve parameter estimation for individuals with limited data
They allow us to examine correlations between individual parameters
They provide population-level insights about general tendencies

In this section, we’ll develop multilevel versions of both our simple beta-binomial and weighted beta-binomial models.

11.19.1 Simulating Data from Multiple Agents

First, let’s simulate a population of agents with varying evidence-weighting parameters:

# Simulation parameters
n_agents <- 20        # Number of agents per model
n_trials_per_agent <- 36  # Number of evidence combinations per agent

# Define population parameters for simple model (equal weights with varying scaling)
simple_population_scaling_mean <- 1.0    # Mean scaling factor (log-scale)
simple_population_scaling_sd <- 0.3      # SD of scaling factor (log-scale)

# Define population parameters for weighted model
weighted_population_scaling_mean <- 1.5   # Mean scaling factor (log-scale)
weighted_population_scaling_sd <- 0.3     # SD of scaling factor (log-scale)
weighted_population_ratio_mean <- 1     # Mean weight ratio (log-scale, 0 = equal weights)
weighted_population_ratio_sd <- 0.5       # SD of weight ratio (log-scale)

# Generate agent parameters for simple model
simple_agents <- tibble(
  agent_id = 1:n_agents,
  model_type = "simple",
  # Generate log-normal scaling factors
  log_scaling = rnorm(n_agents, simple_population_scaling_mean, simple_population_scaling_sd),
  scaling_factor = exp(log_scaling),
  # For simple model, weight ratio is always 1 (equal weights)
  weight_ratio = rep(1, n_agents),
  # Calculate the actual weights
  weight_direct = scaling_factor * weight_ratio / (1 + weight_ratio),
  weight_social = scaling_factor / (1 + weight_ratio)
)

# Generate agent parameters for weighted model
weighted_agents <- tibble(
  agent_id = n_agents + (1:n_agents),  # Continue numbering from simple agents
  model_type = "weighted",
  # Generate log-normal scaling factors
  log_scaling = rnorm(n_agents, weighted_population_scaling_mean, weighted_population_scaling_sd),
  scaling_factor = exp(log_scaling),
  # Generate log-normal weight ratios
  log_weight_ratio = rnorm(n_agents, weighted_population_ratio_mean, weighted_population_ratio_sd),
  weight_ratio = exp(log_weight_ratio),
  # Calculate the actual weights
  weight_direct = scaling_factor * weight_ratio / (1 + weight_ratio),
  weight_social = scaling_factor / (1 + weight_ratio)
)

# Combine agent parameters
all_agents <- bind_rows(simple_agents, weighted_agents)

# Print summary of agent parameters
agent_summary <- all_agents %>%
  group_by(model_type) %>%
  summarize(
    n = n(),
    mean_scaling = mean(scaling_factor),
    sd_scaling = sd(scaling_factor),
    mean_ratio = mean(weight_ratio),
    sd_ratio = sd(weight_ratio),
    mean_direct = mean(weight_direct),
    sd_direct = sd(weight_direct),
    mean_social = mean(weight_social),
    sd_social = sd(weight_social)
  )

print(agent_summary)

## # A tibble: 2 × 10
##   model_type     n mean_scaling sd_scaling mean_ratio sd_ratio mean_direct sd_direct
##   <chr>      <int>        <dbl>      <dbl>      <dbl>    <dbl>       <dbl>     <dbl>
## 1 simple        20         2.94      0.878       1        0           1.47     0.439
## 2 weighted      20         4.56      1.08        3.28     1.67        3.37     0.881
## # ℹ 2 more variables: mean_social <dbl>, sd_social <dbl>

# Create all possible evidence combinations
evidence_combinations <- expand_grid(
  blue1 = 0:8,     # Direct evidence: 0-8 blue marbles out of 8
  blue2 = 0:3,     # Social evidence: 0-3 blue signals out of 3
  total1 = 8,      # Total marbles in direct evidence (constant)
  total2 = 3       # Total signals in social evidence (constant)
)

# Function to generate agent decisions based on their parameters
generate_agent_decisions <- function(agent_data, evidence_df, n_samples = 5) {
  # Extract agent parameters
  agent_id <- agent_data$agent_id
  model_type <- agent_data$model_type
  weight_direct <- agent_data$weight_direct
  weight_social <- agent_data$weight_social
  
  # Create a data frame that repeats each evidence combination n_samples times
  repeated_evidence <- evidence_df %>%
    slice(rep(1:n(), each = n_samples)) %>%
    group_by(blue1, blue2, total1, total2) %>%
    mutate(sample_id = 1:n()) %>%
    ungroup()
  
  # Generate decisions for each evidence combination
  decisions <- pmap_dfr(repeated_evidence, function(blue1, blue2, total1, total2, sample_id) {
    # Calculate weighted evidence
    weighted_blue1 <- blue1 * weight_direct
    weighted_red1 <- (total1 - blue1) * weight_direct
    weighted_blue2 <- blue2 * weight_social
    weighted_red2 <- (total2 - blue2) * weight_social
    
    # Calculate Beta parameters
    alpha_post <- 1 + weighted_blue1 + weighted_blue2
    beta_post <- 1 + weighted_red1 + weighted_red2
    
    # Expected probability
    expected_rate <- alpha_post / (alpha_post + beta_post)
    
    # Make choice
    choice <- rbinom(1, 1, expected_rate)
    
    # Return decision data
    tibble(
      agent_id = agent_id,
      model_type = model_type,
      sample_id = sample_id,
      blue1 = blue1,
      blue2 = blue2,
      total1 = total1,
      total2 = total2,
      expected_rate = expected_rate,
      choice = choice,
      
      # Include true parameter values for reference
      true_weight_direct = weight_direct,
      true_weight_social = weight_social,
      true_weight_ratio = weight_direct / weight_social,
      true_scaling_factor = weight_direct + weight_social
    )
  })
  
  return(decisions)
}

# Generate decisions for all agents
multilevel_sim_data <- map_dfr(1:nrow(all_agents), function(i) {
  generate_agent_decisions(all_agents[i, ], evidence_combinations)
})

# Add descriptive labels
multilevel_sim_data <- multilevel_sim_data %>%
  mutate(
    social_evidence = factor(
      blue2,
      levels = 0:3,
      labels = c("Clear Red", "Weak Red", "Weak Blue", "Clear Blue")
    )
  )

# Visualize decision patterns for selected agents
# Take a sample of agents from each model type
selected_simple_agents <- sample(unique(simple_agents$agent_id), 3)
selected_weighted_agents <- sample(unique(weighted_agents$agent_id), 3)
selected_agents <- c(selected_simple_agents, selected_weighted_agents)

# Create plot
decision_plot <- multilevel_sim_data %>%
  filter(agent_id %in% selected_agents) %>%
  ggplot(aes(x = blue1, y = expected_rate, color = social_evidence, group = social_evidence)) +
  geom_line(size = 1) +
  geom_point(size = 2) +
  geom_hline(yintercept = 0.5, linetype = "dashed", color = "gray50") +
  facet_wrap(~ model_type + agent_id, ncol = 3) +
  labs(
    title = "Decision Patterns: Simple vs. Weighted Integration",
    subtitle = "Simple model shows parallel curves (equal weights), weighted model shows varying influence of social evidence",
    x = "Blue Marbles in Direct Evidence (out of 8)",
    y = "Probability of Choosing Blue",
    color = "Social Evidence"
  ) +
  theme_bw() +
  theme(legend.position = "bottom")

# Display plot
print(decision_plot)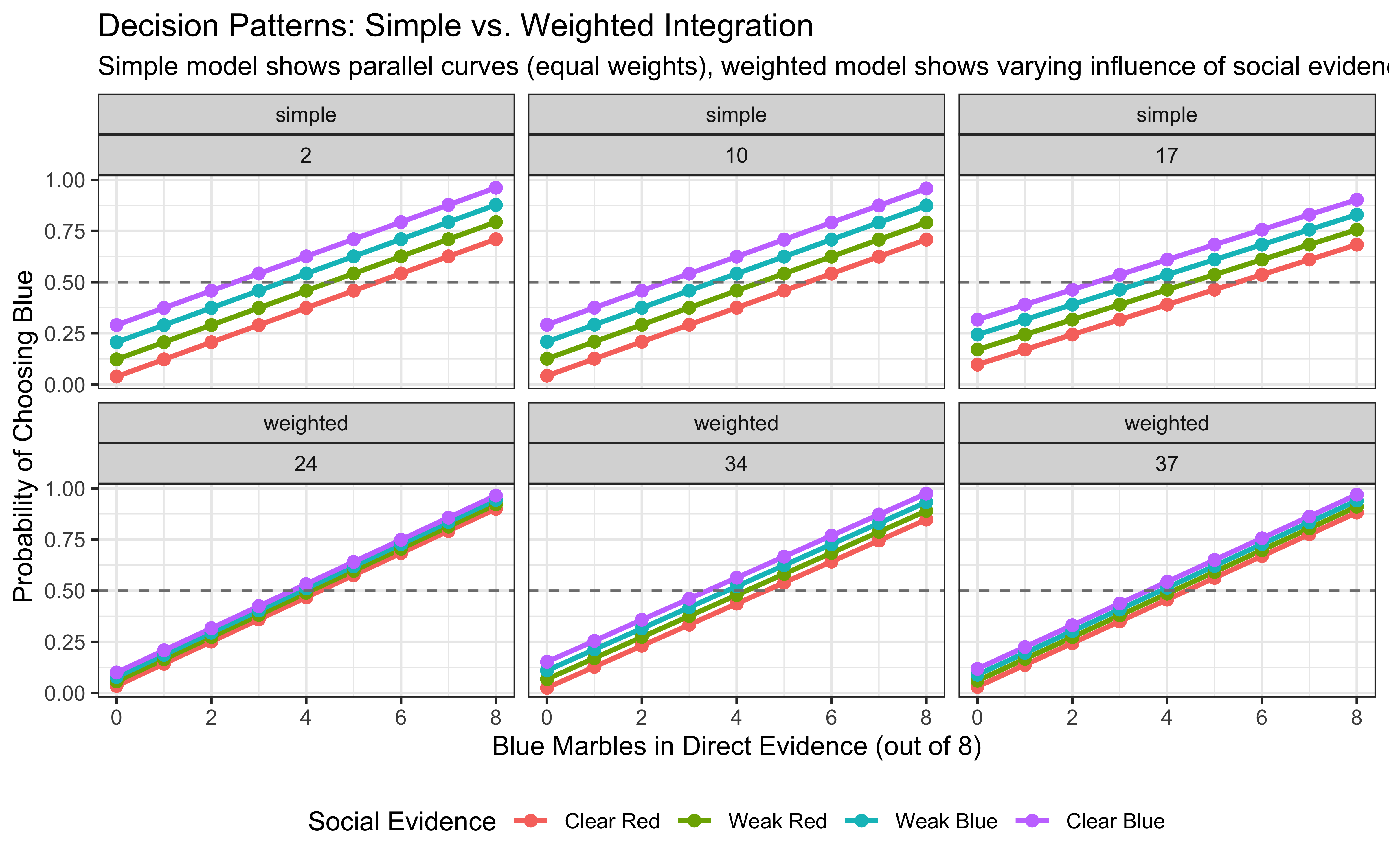

# Print summary of dataset
cat("Generated", nrow(multilevel_sim_data), "observations from", 
    n_agents * 2, "agents (", n_agents, "per model type)\n")

## Generated 7200 observations from 40 agents ( 20 per model type)

# Create data structure for Stan fitting
stan_data_multilevel <- list(
  N = nrow(multilevel_sim_data),
  J = n_agents * 2,
  agent_id = multilevel_sim_data$agent_id,
  choice = multilevel_sim_data$choice,
  blue1 = multilevel_sim_data$blue1,
  total1 = multilevel_sim_data$total1,
  blue2 = multilevel_sim_data$blue2,
  total2 = multilevel_sim_data$total2
)

11.19.2 Understanding the Simulated Data

The simulation generates data from two types of agents:

Simple Integration Agents: These agents weight direct and social evidence equally, but with varying overall scaling factors. This creates individual differences in how strongly evidence affects beliefs, but without preferential weighting of sources.
Weighted Integration Agents: These agents can weight direct and social evidence differently. Some might trust their direct evidence more, others might be more influenced by social information.

The key visual difference in their decision patterns is:

Simple integration agents show parallel curves for different social evidence levels. The spacing between curves is consistent across all levels of direct evidence, indicating equal influence.
Weighted integration agents show varying spacing between curves. When an agent weights social evidence more heavily, the curves are more separated; when direct evidence is weighted more, the curves converge.

By generating data from both models, we can:

Verify our model-fitting procedure can recover the true parameters
Test whether our model comparison methods correctly identify which integration strategy generated each dataset
Assess how robustly we can detect differential weighting of evidence sources

In the next section, we’ll fit both our multilevel models to this data and compare their performance..

Looking at these visualizations, we can see clear individual differences in how agents integrate evidence:

Some agents give more weight to direct evidence, requiring less direct evidence to choose “blue” regardless of social evidence
Others are more influenced by social information, showing greater spacing between the different social evidence lines
These differences create unique decision boundaries for each agent, where they transition from choosing red to blue

11.20 Multilevel Bayesian Models for Evidence Integration

In this section, we implement two multilevel Bayesian models that capture different hypotheses about how individuals integrate evidence from multiple sources. Both models allow for individual differences, but they differ in what aspects of evidence integration can vary across individuals.

11.20.1 Model 1: Simple Evidence Integration with Individual Scaling

Our first model implements a cognitively simple integration strategy where all evidence sources are weighted equally (taken at “face value”), but the overall impact of evidence can vary across individuals:

Each information source (direct and social evidence) receives equal relative weight in the integration process
However, the overall scaling of evidence can vary between individuals
This represents individuals who treat all evidence sources as equally reliable, but differ in how strongly any evidence influences their beliefs

Mathematically, this means that for individual j: - Direct evidence weight = scaling_factor[j] × 0.5 - Social evidence weight = scaling_factor[j] × 0.5

This model captures the hypothesis that individuals differ in their overall sensitivity to evidence, but not in how they relatively weight different sources. Some individuals might be more conservative (low scaling factor), requiring more evidence to shift their beliefs, while others might be more responsive to evidence overall (high scaling factor).

11.20.2 Model 2: Weighted Evidence Integration

Our second model implements a more complex integration strategy where both the overall impact of evidence and the relative weighting of different evidence sources can vary across individuals:

Each individual can give different weights to direct versus social evidence
The overall scaling of evidence can also vary between individuals
This represents individuals who may trust certain evidence sources more than others

We parameterize this model using two key parameters for each individual j: - scaling_factor[j]: The total weight given to all evidence - weight_ratio[j]: The ratio of direct evidence weight to social evidence weight

From these, we derive the actual weights: - Direct evidence weight = scaling_factor[j] × weight_ratio[j] / (1 + weight_ratio[j]) - Social evidence weight = scaling_factor[j] / (1 + weight_ratio[j])

This parameterization ensures that the sum of weights equals the scaling factor, while the ratio between weights is determined by the weight ratio.

11.20.3 Why Allow Scaling to Vary in the Simple Model?

Including individual variation in the scaling factor for the simple model serves several important purposes:

Fair Comparison: It ensures that the comparison between models focuses specifically on differential weighting rather than just the presence of individual differences. The key question becomes “Do individuals weight evidence sources differently?” rather than “Do individuals vary in how they use evidence?”
Statistical Control: The scaling parameter serves as a statistical control, ensuring that any evidence for differential weighting isn’t just capturing overall differences in evidence sensitivity.
Nested Model Structure: It creates a proper nested model relationship - the simple model is a special case of the weighted model where the weight ratio is constrained to be 1.0 (equal weights) for everyone.

This approach allows us to conduct a more precise test of our cognitive hypothesis about differential weighting of evidence sources, while accounting for individual differences in overall evidence use that likely exist regardless of weighting strategy.

11.21 From Single-Agent to Multilevel: Extending Bayesian Cognitive Models

When moving from single-agent to multilevel modeling, we need to extend our Stan code to capture both population-level patterns and individual differences. This transformation requires careful consideration of parameter structure, prior specification, and computational efficiency. Let’s explore how we adapted our single-agent models into multilevel versions.

11.21.1 Key Components of the Multilevel Extension

Parameterizing Individual Differences

In our single-agent models, we had straightforward parameters like total_weight and weight_prop (for the weighted model) or just a scaling factor (for the simple model). For multilevel modeling, we need to create parameters that vary across individuals while maintaining population coherence.

For the simple integration model:

// Single-agent version
parameters {
  real<lower=0> total_weight;         // Overall scaling of evidence
}

// Multilevel version
parameters {
  real mu_scaling;                    // Population mean (log scale)
  real<lower=0> sigma_scaling;        // Population SD
  vector[J] z_scaling;                // Standardized individual deviations
}

transformed parameters {
  vector<lower=0>[J] scaling_factor;  // Individual scaling factors
  
  for (j in 1:J) {
    scaling_factor[j] = exp(mu_scaling + z_scaling[j] * sigma_scaling);
  }
}

Note several key changes:

We now have population-level parameters (mu_scaling, sigma_scaling) that describe the distribution from which individual parameters are drawn
We use non-centered parameterization with standardized z-scores to improve sampling efficiency
We work in log space to ensure positive scaling factors

11.21.2 2. Hierarchical Prior Structure

Priors also need to be restructured in a hierarchical fashion:


// Single-agent version
target += lognormal_lpdf(total_weight | .8, .4);  // Prior for scaling

// Multilevel version
target += normal_lpdf(mu_scaling | 0, 1);        // Prior for population mean
target += exponential_lpdf(sigma_scaling | 2);   // Prior for between-subject variability
target += std_normal_lpdf(z_scaling);            // Prior for standardized deviations

The prior structure now has:

Priors on population means
Priors on population variances
Standard normal priors on the standardized individual deviations

This creates a proper hierarchical structure where individual parameters are partially pooled toward the population mean, with the degree of pooling determined by the population variance.

11.21.3 3. Handling Data from Multiple Individuals

The data structure must be modified to associate observations with specific individuals:

// Single-agent version
data {
  int<lower=1> N;                    // Number of observations
  array[N] int<lower=0, upper=1> choice; // Choices (0=red, 1=blue)
  // Other data...
}

// Multilevel version
data {
  int<lower=1> N;                    // Number of observations
  int<lower=1> J;                    // Number of subjects
  array[N] int<lower=1, upper=J> agent_id; // Agent ID for each observation
  array[N] int<lower=0, upper=1> choice;   // Choices (0=red, 1=blue)
  // Other data...
}

The key addition is agent_id, which maps each observation to its corresponding agent. This allows us to apply the correct individual-level parameters to each observation.

11.21.4 4. Likelihood Specification

The likelihood must be adapted to use the appropriate individual-level parameters:

// Single-agent version
for (i in 1:N) {
  real weighted_blue1 = blue1[i] * weight_direct;
  // ...additional code...
  choice[i] ~ bernoulli(expected_prob);
}

// Multilevel version
for (i in 1:N) {
  real w_direct = weight_direct[agent_id[i]];  // Get parameters for this individual
  real w_social = weight_social[agent_id[i]];
  
  real weighted_blue1 = blue1[i] * w_direct;
  // ...additional code...
  choice[i] ~ bernoulli(expected_prob);
}

We now index individual parameters by agent_id[i] to ensure each observation uses the correct agent’s parameters.

11.21.5 Why These Changes Matter

11.21.5.1 Computational Efficiency: Non-Centered Parameterization

The non-centered parameterization (using z-scores) is critical for efficient sampling in hierarchical models. When individual parameters are close to the population mean or when population variance is small, direct parameterization can cause the sampler to get stuck in a difficult geometry called the “funnel” problem.

By separating the individual effects into standardized z-scores, we create better sampling geometry and improve convergence.

This is why we use:

scaling_factor[j] = exp(mu_scaling + z_scaling[j] * sigma_scaling);

instead of directly sampling individual parameters.

11.21.5.2 Working in Log Space for Bounded Parameters

For parameters that must be positive (like scaling factors), working in log space ensures we maintain proper bounds while allowing the parameter to vary freely on the unconstrained scale:

// This ensures scaling_factor is always positive
scaling_factor[j] = exp(mu_scaling + z_scaling[j] * sigma_scaling);

Similarly, for parameters constrained between 0 and 1 (like weight_prop), we use the logit transformation.

Now we are ready for the full implementation of our multilevel Bayesian models for evidence integration.

# Stan model for multilevel simple beta-binomial
multilevel_simple_stan <- "
// Multilevel Simple Beta-Binomial Model
// This model assumes equal weights for evidence sources (taking evidence at face value)
// but allows for individual variation in overall responsiveness

data {
  int<lower=1> N;                        // Total number of observations
  int<lower=1> J;                        // Number of subjects
  array[N] int<lower=1, upper=J> agent_id;  // Agent ID for each observation
  array[N] int<lower=0, upper=1> choice; // Choices (0=red, 1=blue)
  array[N] int<lower=0> blue1;           // Direct evidence (blue marbles)
  array[N] int<lower=0> total1;          // Total direct evidence
  array[N] int<lower=0> blue2;           // Social evidence (blue signals)
  array[N] int<lower=0> total2;          // Total social evidence
}

parameters {
  // Population-level parameters for agents' preconceptions
  real mu_alpha_prior;                   // Population mean for alpha prior
  real<lower=0> sigma_alpha_prior;       // Population SD for alpha prior
  real mu_beta_prior;                    // Population mean for beta prior
  real<lower=0> sigma_beta_prior;        // Population SD for beta prior
  
  // Population-level parameter for overall scaling
  real mu_scaling;                       // Population mean scaling factor (log scale)
  real<lower=0> sigma_scaling;           // Population SD of scaling
  
  // Individual-level (random) effects
  vector[J] z_alpha_prior;               // Standardized individual deviations for alpha prior
  vector[J] z_beta_prior;                // Standardized individual deviations for beta prior
  vector[J] z_scaling;                   // Standardized individual deviations
  
}

transformed parameters {
  // Individual-level parameters
  vector<lower=0>[J] scaling_factor;     // Individual scaling factors
  vector<lower=0>[J] alpha_prior;        // Individual alpha prior
  vector<lower=0>[J] beta_prior;         // Individual beta prior
  
  // Non-centered parameterization for scaling factor
  for (j in 1:J) {
    alpha_prior[j] = exp(mu_alpha_prior + z_alpha_prior[j] * sigma_alpha_prior);
    beta_prior[j] = exp(mu_beta_prior + z_beta_prior[j] * sigma_beta_prior);
    scaling_factor[j] = exp(mu_scaling + z_scaling[j] * sigma_scaling);
  }
}

model {
  // Priors for population parameters
  target += lognormal_lpdf(mu_alpha_prior | 0, 1);         // Prior for population mean of alpha prior
  target += exponential_lpdf(sigma_alpha_prior | 1);       // Prior for population SD of alpha prior
  target += lognormal_lpdf(mu_beta_prior | 0, 1);          // Prior for population mean of beta prior
  target += exponential_lpdf(sigma_beta_prior | 1);        // Prior for population SD of beta prior
  target += normal_lpdf(mu_scaling | 0, 1);             // Prior for log scaling factor
  target += exponential_lpdf(sigma_scaling | 2);        // Prior for between-subject variability
  
  // Prior for standardized random effects
  z_scaling ~ std_normal();              // Standard normal prior
  z_alpha_prior ~ std_normal();          // Standard normal prior
  z_beta_prior ~ std_normal();           // Standard normal prior
  
  // Likelihood
  for (i in 1:N) {
    // Calculate the individual scaling factor
    real scale = scaling_factor[agent_id[i]];
    
    // Simple integration - weights both evidence sources equally but applies individual scaling
    // Both direct and social evidence get weight = 1.0 * scaling_factor
    real weighted_blue1 = blue1[i] * scale;
    real weighted_red1 = (total1[i] - blue1[i]) * scale;
    real weighted_blue2 = blue2[i] * scale;
    real weighted_red2 = (total2[i] - blue2[i]) * scale;
    
    // Calculate Beta parameters for posterior
    real alpha_post = alpha_prior[agent_id[i]] + weighted_blue1 + weighted_blue2;
    real beta_post = beta_prior[agent_id[i]] + weighted_red1 + weighted_red2;
    
    // Use beta-binomial distribution to model the choice
    target += beta_binomial_lpmf(choice[i] | 1, alpha_post, beta_post);
  }
}

generated quantities {
  // Population parameters on natural scale
  real population_scaling = exp(mu_scaling);
  
  // Log likelihood for model comparison
  vector[N] log_lik;
  
  // Population and individual predictions
  array[N] int pred_choice;
  
  for (i in 1:N) {
    // Calculate the individual scaling factor
    real scale = scaling_factor[agent_id[i]];
    
    // Calculate weighted evidence
    real weighted_blue1 = blue1[i] * scale;
    real weighted_red1 = (total1[i] - blue1[i]) * scale;
    real weighted_blue2 = blue2[i] * scale;
    real weighted_red2 = (total2[i] - blue2[i]) * scale;
    
    // Calculate Beta parameters
    real alpha_post = alpha_prior[agent_id[i]] + weighted_blue1 + weighted_blue2;
    real beta_post = beta_prior[agent_id[i]] + weighted_red1 + weighted_red2;
    
    // Generate predictions using beta-binomial
    pred_choice[i] = beta_binomial_rng(1, alpha_post, beta_post);
    
    // Calculate log likelihood
    log_lik[i] = beta_binomial_lpmf(choice[i] | 1, alpha_post, beta_post);
  }
}
"

# Write the model to a file
write_stan_file(
  multilevel_simple_stan,
  dir = "stan/",
  basename = "W10_multilevel_simple_beta_binomial.stan"
)

## [1] "/Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/stan/W10_multilevel_simple_beta_binomial.stan"

11.21.6 Implementing the Multilevel Weighted Beta-Binomial Model in Stan

Now let’s implement the multilevel weighted beta-binomial model, which allows both population-level estimates of evidence weights and individual variations around these population means.

multilevel_weighted_stan <- "
// Multilevel Weighted Beta-Binomial Model
// This model allows different weights for different evidence sources
// Using total_weight and weight_prop parameterization

data {
  int<lower=1> N;                        // Total number of observations
  int<lower=1> J;                        // Number of subjects
  array[N] int<lower=1, upper=J> agent_id;  // Agent ID for each observation
  array[N] int<lower=0, upper=1> choice; // Choices (0=red, 1=blue)
  array[N] int<lower=0> blue1;           // Direct evidence (blue marbles)
  array[N] int<lower=0> total1;          // Total direct evidence
  array[N] int<lower=0> blue2;           // Social evidence (blue signals)
  array[N] int<lower=0> total2;          // Total social evidence
}

parameters {
  
  // Population-level parameters for agents' preconceptions
  real mu_alpha_prior;                   // Population mean for alpha prior
  real<lower=0> sigma_alpha_prior;       // Population SD for alpha prior
  real mu_beta_prior;                    // Population mean for beta prior
  real<lower=0> sigma_beta_prior;        // Population SD for beta prior
  
  // Population-level parameters
  real mu_weight_ratio;                  // Population mean for relative weight (direct/social) - log scale
  real mu_scaling;                       // Population mean for overall scaling - log scale
  
  // Population-level standard deviations
  real<lower=0> sigma_weight_ratio;      // Between-subject variability in relative weighting
  real<lower=0> sigma_scaling;           // Between-subject variability in scaling
  
  // Individual-level (random) effects
  vector[J] z_weight_ratio;              // Standardized individual weight ratio deviations
  vector[J] z_scaling;                   // Standardized individual scaling deviations
}

transformed parameters {
  // Individual-level parameters
  vector<lower=0>[J] weight_ratio;       // Individual relative weights (direct/social)
  vector<lower=0>[J] scaling_factor;     // Individual overall scaling factors
  vector<lower=0>[J] weight_direct;      // Individual weights for direct evidence
  vector<lower=0>[J] weight_social;      // Individual weights for social evidence
  
  // Non-centered parameterization
  for (j in 1:J) {
    // Transform standardized parameters to natural scale
    weight_ratio[j] = exp(mu_weight_ratio + z_weight_ratio[j] * sigma_weight_ratio);
    scaling_factor[j] = exp(mu_scaling + z_scaling[j] * sigma_scaling);
    
    // Calculate individual weights
    // The sum of weights is determined by the scaling factor
    // The ratio between weights is determined by weight_ratio
    weight_direct[j] = scaling_factor[j] * weight_ratio[j] / (1 + weight_ratio[j]);
    weight_social[j] = scaling_factor[j] / (1 + weight_ratio[j]);
  }
}

model {
  // Priors for population parameters
  mu_weight_ratio ~ normal(0, 1);        // Prior for log weight ratio centered at 0 (equal weights)
  mu_scaling ~ normal(0, 1);             // Prior for log scaling factor
  
  sigma_weight_ratio ~ exponential(2);   // Prior for between-subject variability
  sigma_scaling ~ exponential(2);        // Prior for scaling variability
  
  // Priors for individual random effects
  z_weight_ratio ~ std_normal();         // Standard normal prior for weight ratio z-scores
  z_scaling ~ std_normal();              // Standard normal prior for scaling z-scores
  z_alpha_prior ~ std_normal();          // Standard normal prior
  z_beta_prior ~ std_normal();           // Standard normal prior
  
  // Likelihood
  for (i in 1:N) {
    // Get weights for this person
    real w_direct = weight_direct[agent_id[i]];
    real w_social = weight_social[agent_id[i]];
    
    // Calculate weighted evidence
    real weighted_blue1 = blue1[i] * w_direct;
    real weighted_red1 = (total1[i] - blue1[i]) * w_direct;
    real weighted_blue2 = blue2[i] * w_social;
    real weighted_red2 = (total2[i] - blue2[i]) * w_social;
    
    // Calculate Beta parameters for Bayesian integration
    real alpha_post = alpha_prior[agent_id[i]] + weighted_blue1 + weighted_blue2;
    real beta_post = beta_prior[agent_id[i]] + weighted_red1 + weighted_red2;
    
    // Use beta-binomial distribution to model the choice
    target += beta_binomial_lpmf(choice[i] | 1, alpha_post, beta_post);
  }
}

generated quantities {
  // Convert population parameters to original weight scale for interpretation
  real population_ratio = exp(mu_weight_ratio);
  real population_scaling = exp(mu_scaling);
  real population_weight_direct = population_scaling * population_ratio / (1 + population_ratio);
  real population_weight_social = population_scaling / (1 + population_ratio);
  
  // Log likelihood for model comparison
  vector[N] log_lik;
  
  // Population and individual predictions
  array[N] int pred_choice;
  
  for (i in 1:N) {
    // Get weights for this person
    real w_direct = weight_direct[agent_id[i]];
    real w_social = weight_social[agent_id[i]];
    
    // Calculate weighted evidence
    real weighted_blue1 = blue1[i] * w_direct;
    real weighted_red1 = (total1[i] - blue1[i]) * w_direct;
    real weighted_blue2 = blue2[i] * w_social;
    real weighted_red2 = (total2[i] - blue2[i]) * w_social;
    
    // Calculate Beta parameters
    real alpha_post = alpha_prior[agent_id[i]] + weighted_blue1 + weighted_blue2;
    real beta_post = beta_prior[agent_id[i]] + weighted_red1 + weighted_red2;
    
    // Generate predictions using beta-binomial
    pred_choice[i] = beta_binomial_rng(1, alpha_post, beta_post);
    
    // Calculate log likelihood
    log_lik[i] = beta_binomial_lpmf(choice[i] | 1, alpha_post, beta_post);
  }
}
"
# Write the model to a file
write_stan_file(
  multilevel_weighted_stan,
  dir = "stan/",
  basename = "W10_multilevel_weighted_beta_binomial.stan"
)

## [1] "/Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/stan/W10_multilevel_weighted_beta_binomial.stan"

11.22 Fitting the Multilevel Models

Now that we’ve generated data from both simple and weighted integration strategies, we can fit our two multilevel models to this data. This will allow us to:

Evaluate our ability to recover the true parameters
Compare the models to determine which better explains the observed decisions
Assess whether we can correctly identify which cognitive strategy generated each agent’s data

We’ll fit both models to the full dataset, which contains a mixture of simple and weighted integration agents. This represents a realistic scenario where we don’t know in advance which strategy each individual is using.

# Fitting the Multilevel Models to Simulated Data
# We'll fit both the simple and weighted integration models to our simulated data

# Create file paths for Stan models
file_simple_ml <- file.path("stan/W10_multilevel_simple_beta_binomial.stan")
file_weighted_ml <- file.path("stan/W10_multilevel_weighted_beta_binomial.stan")

# Check if we need to regenerate model fits or load existing ones
if (regenerate_simulations) {
  # Compile Stan models
  mod_simple_ml <- cmdstan_model(
    file_simple_ml, 
    cpp_options = list(stan_threads = TRUE)
  )
  
  mod_weighted_ml <- cmdstan_model(
    file_weighted_ml, 
    cpp_options = list(stan_threads = TRUE)
  )
  
  # Fit the simple multilevel model
  # This model assumes equal weights for evidence sources but allows individual scaling
  cat("Fitting the simple multilevel model...\n")
  
  fit_simple_ml <- mod_simple_ml$sample(
    data = stan_data_multilevel,     # Data for all agents (both types)
    seed = 242,                       # Seed for reproducibility
    chains = 2,                      # Number of MCMC chains
    parallel_chains = 2,             # Run chains in parallel
    threads_per_chain = 1,           # Stan threading
    iter_warmup = 1000,              # Warmup iterations
    iter_sampling = 1000,            # Sampling iterations
    refresh = 100,                   # Progress update frequency
    adapt_delta = 0.9,               # Adaptation parameter for HMC
    max_treedepth = 12               # Maximum tree depth for HMC
  )
  
  # Fit the weighted multilevel model
  # This model allows different weights for different evidence sources
  cat("Fitting the weighted multilevel model...\n")
  
  fit_weighted_ml <- mod_weighted_ml$sample(
    data = stan_data_multilevel,     # Same data as simple model
    seed = 143,                       # Different seed
    chains = 2,                      # Number of MCMC chains
    parallel_chains = 2,             # Run chains in parallel
    threads_per_chain = 1,           # Stan threading
    iter_warmup = 1000,              # Warmup iterations
    iter_sampling = 1000,            # Sampling iterations
    refresh = 100,                   # Progress update frequency
    adapt_delta = 0.95,              # Higher adapt_delta for stability
    max_treedepth = 12               # Maximum tree depth for HMC
  )
  
  # Save model fits for future use
  fit_simple_ml$save_object("simmodels/fit_multilevel_simple_mixed.rds")
  fit_weighted_ml$save_object("simmodels/fit_multilevel_weighted_mixed.rds")
  
  cat("Models fitted and saved.\n")
} else {
  # Load existing model fits
  fit_simple_ml <- readRDS("simmodels/fit_multilevel_simple_mixed.rds")
  fit_weighted_ml <- readRDS("simmodels/fit_multilevel_weighted_mixed.rds")
  
  cat("Loaded existing model fits.\n")
}

## Loaded existing model fits.

# Check for convergence issues
# For simple model
simple_summary <- fit_simple_ml$summary()
simple_rhat_issues <- simple_summary %>%
  filter(rhat > 1.05) %>%
  nrow()

# For weighted model
weighted_summary <- fit_weighted_ml$summary()
weighted_rhat_issues <- weighted_summary %>%
  filter(rhat > 1.05) %>%
  nrow()

# Print convergence summary
cat("Convergence check:\n")

## Convergence check:

cat("Simple model parameters with Rhat > 1.05:", simple_rhat_issues, "out of", nrow(simple_summary), "\n")

## Simple model parameters with Rhat > 1.05: 0 out of 14484

cat("Weighted model parameters with Rhat > 1.05:", weighted_rhat_issues, "out of", nrow(weighted_summary), "\n")

## Weighted model parameters with Rhat > 1.05: 0 out of 14649

# Extract posterior samples for key parameters
# From simple model
draws_simple <- as_draws_df(fit_simple_ml$draws())
population_scaling_simple <- mean(exp(draws_simple$mu_scaling))
population_scaling_sd_simple <- mean(draws_simple$sigma_scaling)

# From weighted model
draws_weighted <- as_draws_df(fit_weighted_ml$draws())
population_ratio_weighted <- mean(exp(draws_weighted$mu_weight_ratio))
population_scaling_weighted <- mean(exp(draws_weighted$mu_scaling))
population_ratio_sd_weighted <- mean(draws_weighted$sigma_weight_ratio)
population_scaling_sd_weighted <- mean(draws_weighted$sigma_scaling)

# Print population-level parameter estimates
cat("\nPopulation parameter estimates:\n")

## 
## Population parameter estimates:

cat("Simple model:\n")

## Simple model:

cat("  Mean scaling factor:", round(population_scaling_simple, 2), "\n")

##   Mean scaling factor: 2.3

cat("  SD of log scaling:", round(population_scaling_sd_simple, 2), "\n\n")

##   SD of log scaling: 0.19

cat("Weighted model:\n")

## Weighted model:

cat("  Mean scaling factor:", round(population_scaling_weighted, 2), "\n")

##   Mean scaling factor: 3.29

cat("  Mean weight ratio (direct/social):", round(population_ratio_weighted, 2), "\n")

##   Mean weight ratio (direct/social): 1.56

cat("  SD of log scaling:", round(population_scaling_sd_weighted, 2), "\n")

##   SD of log scaling: 0.18

cat("  SD of log weight ratio:", round(population_ratio_sd_weighted, 2), "\n")

##   SD of log weight ratio: 0.4

11.22.1 Parameter Recovery Analysis

Now that we’ve fitted both models, let’s examine how well we can recover the true individual parameters. This is a crucial step in validating our models - if we can’t recover the parameters that generated our data, we might need to refine our models or collect more data.

# Extract individual parameter estimates from both models
# For simple model (scaling factor only)
scaling_factor_simple <- matrix(NA, nrow = nrow(draws_simple), ncol = n_agents * 2)
for (j in 1:(n_agents * 2)) {
  scaling_factor_simple[, j] <- draws_simple[[paste0("scaling_factor[", j, "]")]]
}

# Calculate posterior means
scaling_factor_simple_est <- colMeans(scaling_factor_simple)

# For weighted model (scaling factor and weight ratio)
scaling_factor_weighted <- matrix(NA, nrow = nrow(draws_weighted), ncol = n_agents * 2)
weight_ratio_weighted <- matrix(NA, nrow = nrow(draws_weighted), ncol = n_agents * 2)
weight_direct_weighted <- matrix(NA, nrow = nrow(draws_weighted), ncol = n_agents * 2)
weight_social_weighted <- matrix(NA, nrow = nrow(draws_weighted), ncol = n_agents * 2)

for (j in 1:(n_agents * 2)) {
  scaling_factor_weighted[, j] <- draws_weighted[[paste0("scaling_factor[", j, "]")]]
  weight_ratio_weighted[, j] <- draws_weighted[[paste0("weight_ratio[", j, "]")]]
  weight_direct_weighted[, j] <- draws_weighted[[paste0("weight_direct[", j, "]")]]
  weight_social_weighted[, j] <- draws_weighted[[paste0("weight_social[", j, "]")]]
}

# Calculate posterior means
scaling_factor_weighted_est <- colMeans(scaling_factor_weighted)
weight_ratio_weighted_est <- colMeans(weight_ratio_weighted)
weight_direct_weighted_est <- colMeans(weight_direct_weighted)
weight_social_weighted_est <- colMeans(weight_social_weighted)

# Create dataframe for recovery analysis
recovery_data <- tibble(
  agent_id = 1:(n_agents * 2),
  model_type = all_agents$model_type,
  
  # True parameters
  true_scaling_factor = all_agents$scaling_factor,
  true_weight_ratio = all_agents$weight_ratio,
  true_weight_direct = all_agents$weight_direct,
  true_weight_social = all_agents$weight_social,
  
  # Estimated from simple model
  est_scaling_simple = scaling_factor_simple_est,
  
  # Estimated from weighted model
  est_scaling_weighted = scaling_factor_weighted_est,
  est_ratio_weighted = weight_ratio_weighted_est,
  est_direct_weighted = weight_direct_weighted_est,
  est_social_weighted = weight_social_weighted_est
)

# Calculate recovery accuracy metrics
recovery_data <- recovery_data %>%
  mutate(
    # Error in scaling factor estimates
    error_scaling_simple = est_scaling_simple - true_scaling_factor,
    pct_error_scaling_simple = 100 * error_scaling_simple / true_scaling_factor,
    
    error_scaling_weighted = est_scaling_weighted - true_scaling_factor,
    pct_error_scaling_weighted = 100 * error_scaling_weighted / true_scaling_factor,
    
    # Error in weight ratio estimates (only for weighted model)
    error_ratio_weighted = est_ratio_weighted - true_weight_ratio,
    pct_error_ratio_weighted = 100 * error_ratio_weighted / true_weight_ratio,
    
    # Error in direct/social weight estimates
    error_direct_weighted = est_direct_weighted - true_weight_direct,
    pct_error_direct_weighted = 100 * error_direct_weighted / true_weight_direct,
    
    error_social_weighted = est_social_weighted - true_weight_social,
    pct_error_social_weighted = 100 * error_social_weighted / true_weight_social
  )

# Summarize recovery errors by agent type
recovery_summary <- recovery_data %>%
  group_by(model_type) %>%
  summarize(
    # Simple model scaling recovery
    mean_abs_error_scaling_simple = mean(abs(error_scaling_simple)),
    mean_abs_pct_error_scaling_simple = mean(abs(pct_error_scaling_simple)),
    
    # Weighted model param recovery
    mean_abs_error_scaling_weighted = mean(abs(error_scaling_weighted)),
    mean_abs_pct_error_scaling_weighted = mean(abs(pct_error_scaling_weighted)),
    
    mean_abs_error_ratio_weighted = mean(abs(error_ratio_weighted)),
    mean_abs_pct_error_ratio_weighted = mean(abs(pct_error_ratio_weighted)),
    
    mean_abs_error_direct_weighted = mean(abs(error_direct_weighted)),
    mean_abs_pct_error_direct_weighted = mean(abs(pct_error_direct_weighted)),
    
    mean_abs_error_social_weighted = mean(abs(error_social_weighted)),
    mean_abs_pct_error_social_weighted = mean(abs(pct_error_social_weighted)),
    .groups = "drop"
  )

# Print recovery summary
knitr::kable(recovery_summary, digits = 2, caption = "Parameter Recovery Accuracy by Agent Type")

Table 11.4: Parameter Recovery Accuracy by Agent Type
model_type	mean_abs_error_scaling_simple	mean_abs_pct_error_scaling_simple	mean_abs_error_scaling_weighted	mean_abs_pct_error_scaling_weighted	mean_abs_error_ratio_weighted	mean_abs_pct_error_ratio_weighted	mean_abs_error_direct_weighted	mean_abs_pct_error_direct_weighted	mean_abs_error_social_weighted	mean_abs_pct_error_social_weighted
simple	0.80	24.90	0.82	33.42	0.45	45.02	0.57	47.45	0.35	25.37
weighted	2.15	44.02	1.24	24.22	1.49	37.50	1.27	35.13	0.41	45.28

# Create visualizations of parameter recovery

# 1. Scaling factor recovery
p1 <- ggplot(recovery_data, aes(x = true_scaling_factor, y = est_scaling_simple, color = model_type)) +
  geom_point(size = 3, alpha = 0.7) +
  geom_abline(intercept = 0, slope = 1, linetype = "dashed") +
  labs(
    title = "Scaling Factor Recovery (Simple Model)",
    subtitle = "How well can the simple model recover the true scaling factors?",
    x = "True Scaling Factor",
    y = "Estimated Scaling Factor",
    color = "Agent Type"
  ) +
  theme_minimal()

p2 <- ggplot(recovery_data, aes(x = true_scaling_factor, y = est_scaling_weighted, color = model_type)) +
  geom_point(size = 3, alpha = 0.7) +
  geom_abline(intercept = 0, slope = 1, linetype = "dashed") +
  labs(
    title = "Scaling Factor Recovery (Weighted Model)",
    subtitle = "How well can the weighted model recover the true scaling factors?",
    x = "True Scaling Factor",
    y = "Estimated Scaling Factor",
    color = "Agent Type"
  ) +
  theme_minimal()

# 2. Weight ratio recovery (weighted model only)
p3 <- ggplot(recovery_data, aes(x = true_weight_ratio, y = est_ratio_weighted, color = model_type)) +
  geom_point(size = 3, alpha = 0.7) +
  geom_abline(intercept = 0, slope = 1, linetype = "dashed") +
  labs(
    title = "Weight Ratio Recovery (Weighted Model)",
    subtitle = "How well can the weighted model recover the true weight ratios?",
    x = "True Weight Ratio (Direct/Social)",
    y = "Estimated Weight Ratio",
    color = "Agent Type"
  ) +
  theme_minimal()

# Arrange plots
recovery_plots <- p1 + p2 + p3 + plot_layout(ncol = 2)
print(recovery_plots)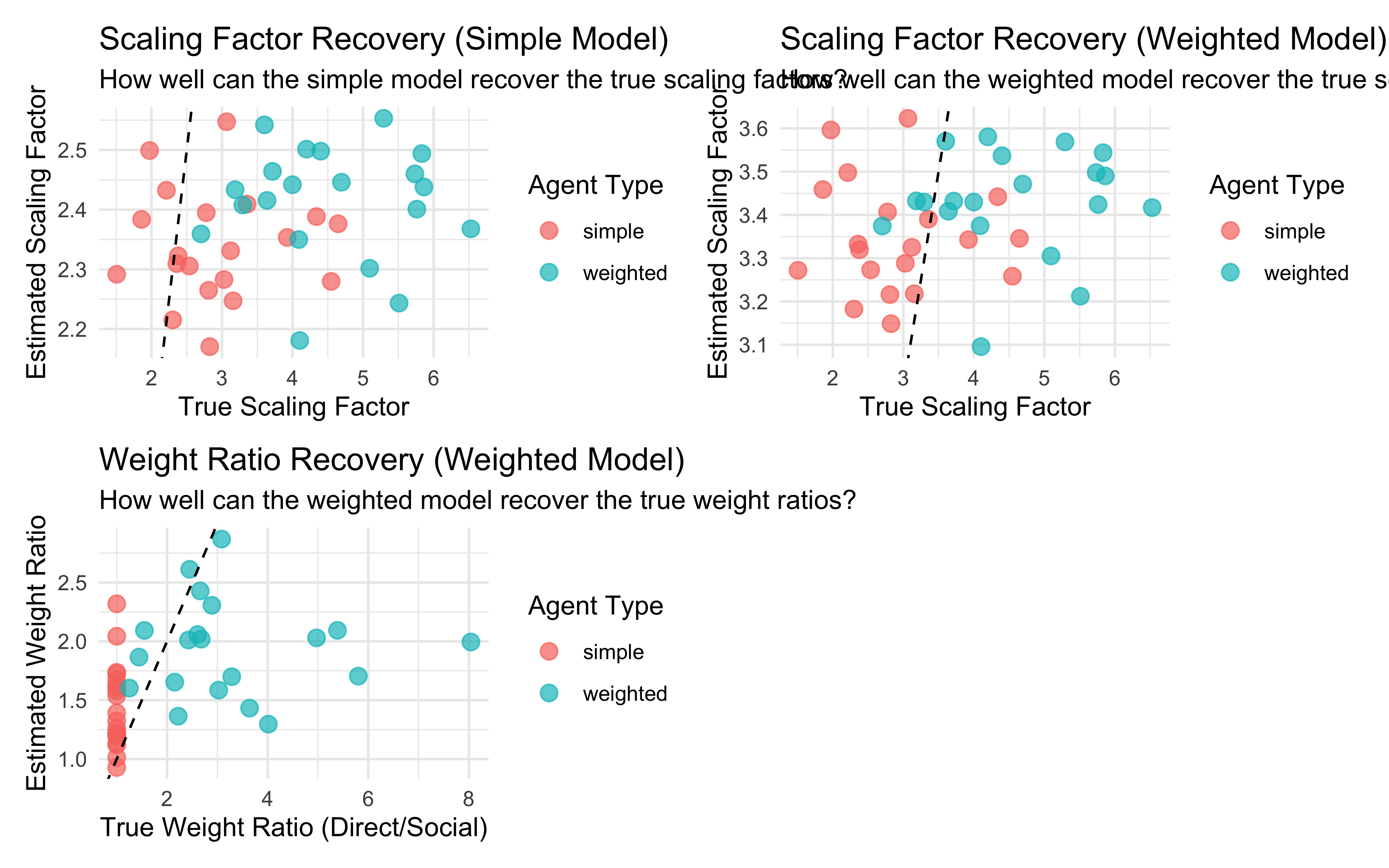

11.22.2 Model Comparison

Now that we’ve fitted both models, we can formally compare them to see which better explains the observed data. We’ll use Leave-One-Out Cross-Validation (LOO-CV) to estimate each model’s predictive accuracy.

In a real application, we wouldn’t know in advance whether individuals use simple or weighted integration strategies. Model comparison helps us determine which cognitive model is more consistent with observed behavior.

# Calculate LOO-CV for model comparison
# This evaluates how well each model predicts held-out data

# For simple model
loo_simple <- fit_simple_ml$loo()

# For weighted model
loo_weighted <- fit_weighted_ml$loo()

# Compare models
loo_comparison <- loo_compare(loo_simple, loo_weighted)
print(loo_comparison)

##        elpd_diff se_diff
## model2   0.0       0.0  
## model1 -21.6       6.7

# Calculate model weights
model_weights <- loo_model_weights(list(
  "Simple Integration" = loo_simple,
  "Weighted Integration" = loo_weighted
))

# Print model weights
print(model_weights)

## Method: stacking
## ------
##                      weight
## Simple Integration   0.028 
## Weighted Integration 0.972

# Create a visualization of model comparison
model_comp_data <- tibble(
  model = names(model_weights),
  weight = as.numeric(model_weights)
)

p_model_comp <- ggplot(model_comp_data, aes(x = model, y = weight, fill = model)) +
  geom_col() +
  geom_text(aes(label = scales::percent(weight, accuracy = 0.1)), 
            vjust = -0.5, size = 5) +
  labs(
    title = "Model Comparison Using LOO-CV",
    subtitle = "Higher weights indicate better predictive performance",
    x = NULL,
    y = "Model Weight"
  ) +
  scale_fill_brewer(palette = "Set1") +
  theme_minimal() +
  theme(legend.position = "none")

print(p_model_comp)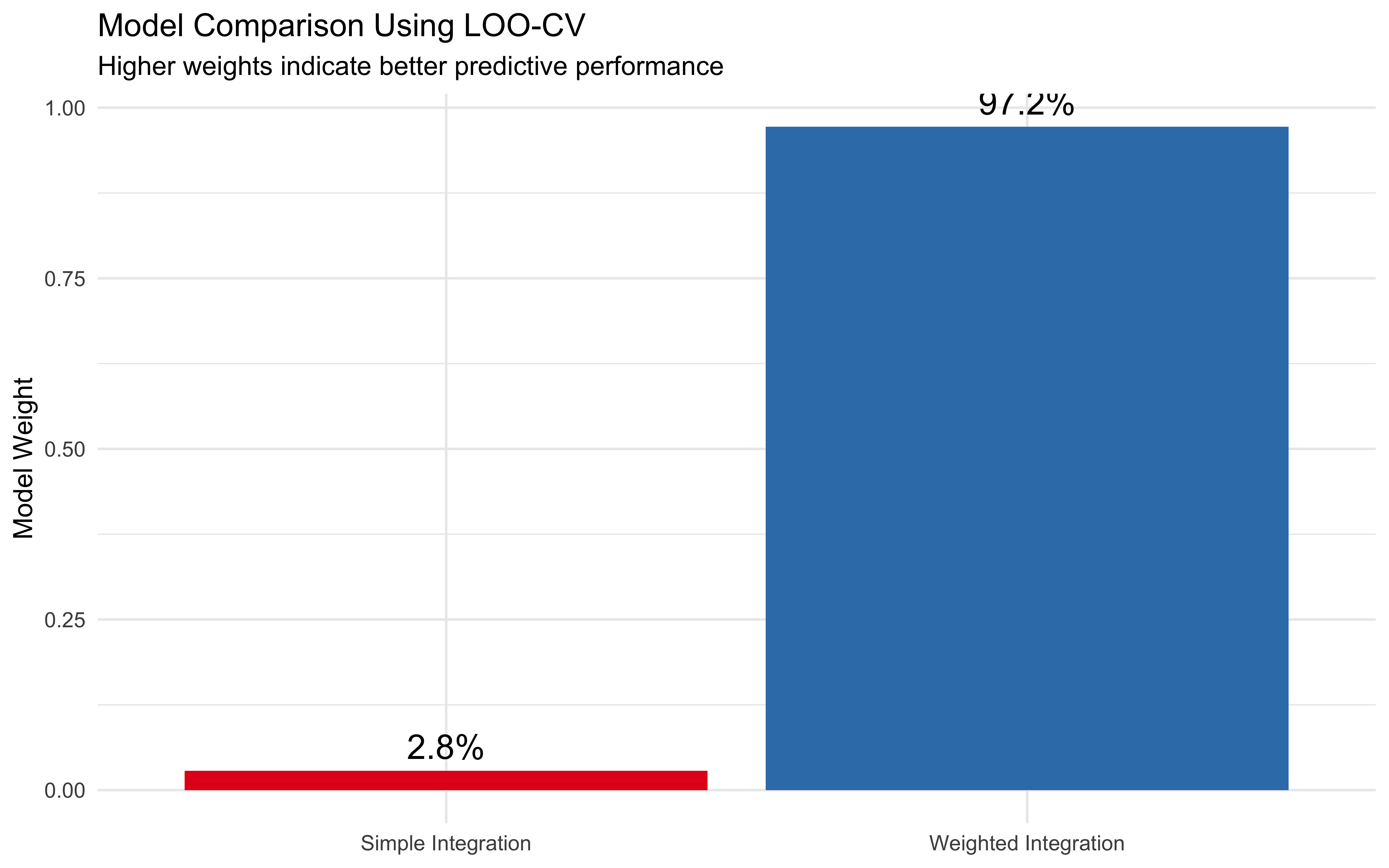

# Compare model performance by agent type
# Calculate pointwise ELPD values for each model
elpd_simple <- loo_simple$pointwise[, "elpd_loo"]
elpd_weighted <- loo_weighted$pointwise[, "elpd_loo"]

# Aggregate by agent
elpd_by_agent <- multilevel_sim_data %>%
  dplyr::select(agent_id, model_type) %>%
  distinct() %>%
  mutate(
    elpd_simple = NA_real_,
    elpd_weighted = NA_real_
  )

# Calculate ELPD sums by agent
for (j in 1:nrow(elpd_by_agent)) {
  agent <- elpd_by_agent$agent_id[j]
  # Find rows for this agent
  agent_rows <- which(multilevel_sim_data$agent_id == agent)
  # Sum ELPD values for this agent
  elpd_by_agent$elpd_simple[j] <- sum(elpd_simple[agent_rows])
  elpd_by_agent$elpd_weighted[j] <- sum(elpd_weighted[agent_rows])
}

# Calculate ELPD difference (positive = weighted model is better)
elpd_by_agent <- elpd_by_agent %>%
  mutate(
    elpd_diff = elpd_weighted - elpd_simple,
    better_model = ifelse(elpd_diff > 0, "Weighted", "Simple")
  )

# Create visualization of model preference by agent type

p_agent_comp <- ggplot(elpd_by_agent, aes(x = agent_id, y = elpd_diff, color = model_type)) +
  geom_point() +
  geom_hline(yintercept = 0, linetype = "dashed") +
  labs(
    title = "Model Preference by Agent Type",
    subtitle = "Positive values favor the weighted model; negative values favor the simple model",
    x = "True Agent Type",
    y = "ELPD Difference (Weighted - Simple)",
    color = "Preferred Model"
  ) +
  theme_minimal()


print(p_agent_comp)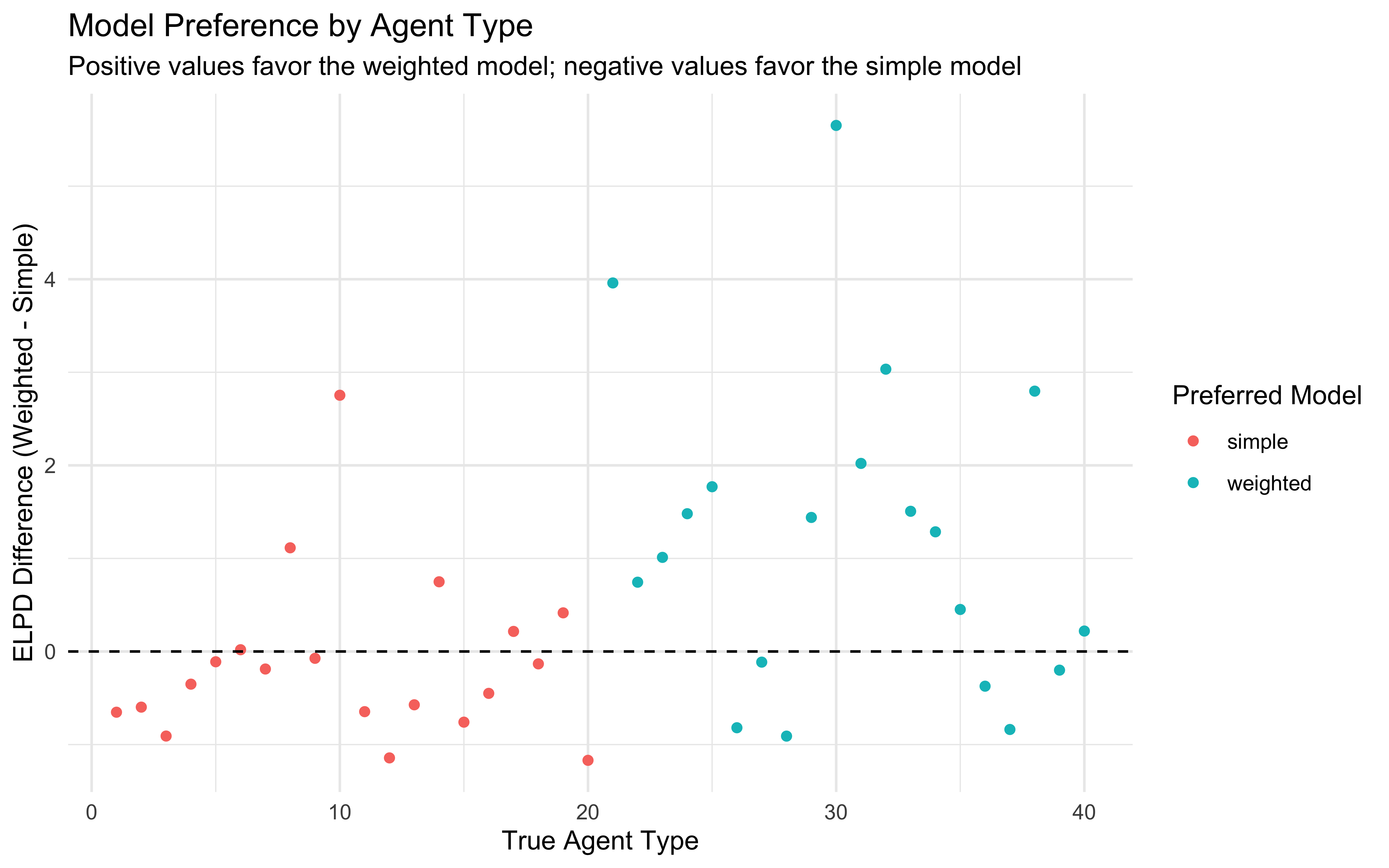

# Calculate classification accuracy
# How often does the better-fitting model match the true generating model?
classification <- elpd_by_agent %>%
  mutate(
    # For simple agents, the simple model should be better
    correct_classification = case_when(
      model_type == "simple" & better_model == "Simple" ~ TRUE,
      model_type == "weighted" & better_model == "Weighted" ~ TRUE,
      TRUE ~ FALSE
    )
  )

# Calculate overall accuracy and by agent type
overall_accuracy <- mean(classification$correct_classification)
accuracy_by_type <- classification %>%
  group_by(model_type) %>%
  summarize(
    n = n(),
    correct = sum(correct_classification),
    accuracy = correct / n,
    .groups = "drop"
  )

# Print classification results
cat("\nModel Classification Accuracy:\n")

## 
## Model Classification Accuracy:

cat("Overall accuracy:", scales::percent(overall_accuracy), "\n\n")

## Overall accuracy: 70%

print(knitr::kable(accuracy_by_type, caption = "Classification Accuracy by Agent Type"))

## 
## 
## Table: (\#tab:unnamed-chunk-64)Classification Accuracy by Agent Type
## 
## |model_type |  n| correct| accuracy|
## |:----------|--:|-------:|--------:|
## |simple     | 20|      14|      0.7|
## |weighted   | 20|      14|      0.7|

11.23 Dynamic Bayesian Evidence Integration: Sequential Updating Models

In real-world learning scenarios, people continuously update their beliefs as they gather new evidence. While our previous models considered decision-making based on static evidence, a more realistic approach is to incorporate sequential updating where beliefs evolve over time. Let’s develop an extension of our Bayesian evidence integration models that captures how agents dynamically update their beliefs across trials.

11.23.1 Sequential Bayesian Updating: The Theoretical Framework

In sequential Bayesian updating, an agent’s posterior belief from one trial becomes the prior for the next trial. This creates a continuous learning process where the agent’s beliefs evolve over time based on observed evidence. The key components of a sequential updating model are:

Initial prior belief - The agent’s belief before encountering any evidence
Trial-by-trial updating - How beliefs are updated after each new piece of evidence
Response mechanism - How updated beliefs translate into observable choices

Let’s implement this framework in Stan, starting with the single-agent version and then extending to a multilevel model.

11.23.2 Single-Agent Sequential Updating Model

# Stan code for a sequential Bayesian updating model
sequential_updating_stan <- "
// Sequential Bayesian Updating Model
// This model tracks how an agent updates beliefs across a sequence of trials
data {
  int<lower=1> T;                        // Number of trials
  array[T] int<lower=0, upper=1> choice; // Choices (0=red, 1=blue)
  array[T] int<lower=0> blue1;           // Direct evidence (blue marbles) on each trial
  array[T] int<lower=0> total1;          // Total direct evidence on each trial
  array[T] int<lower=0> blue2;           // Social evidence (blue signals) on each trial
  array[T] int<lower=0> total2;          // Total social evidence on each trial
}

parameters {
  real<lower=0> total_weight;             // Overall weight given to evidence
  real<lower=0, upper=1> weight_prop;     // Proportion of weight for direct evidence
  real<lower=0> learning;                    // Learning rate parameter
}

transformed parameters {
  // Calculate weights for each evidence source
  real weight_direct = total_weight * weight_prop;
  real weight_social = total_weight * (1 - weight_prop);
  
  // Variables to track belief updating across trials
  vector<lower=0, upper=1>[T] belief;     // Belief in blue on each trial
  vector<lower=0>[T] alpha_param;         // Beta distribution alpha parameter
  vector<lower=0>[T] beta_param;          // Beta distribution beta parameter
  
  // Initial belief parameters (uniform prior)
  alpha_param[1] = 1.0;
  beta_param[1] = 1.0;
  
  // Calculate belief for first trial
  belief[1] = alpha_param[1] / (alpha_param[1] + beta_param[1]);
  
  // Update beliefs across trials
  for (t in 2:T) {
    // Calculate weighted evidence from previous trial
    real weighted_blue1 = blue1[t-1] * weight_direct;
    real weighted_red1 = (total1[t-1] - blue1[t-1]) * weight_direct;
    real weighted_blue2 = blue2[t-1] * weight_social;
    real weighted_red2 = (total2[t-1] - blue2[t-1]) * weight_social;
    
    // Update belief with learning rate
    // alpha controls how much new evidence affects the belief
    alpha_param[t] = alpha_param[t-1] + learning * (weighted_blue1 + weighted_blue2);
    beta_param[t] = beta_param[t-1] + learning * (weighted_red1 + weighted_red2);
    
    // Calculate updated belief
    belief[t] = alpha_param[t] / (alpha_param[t] + beta_param[t]);
  }
}

model {
  // Priors for parameters
  target += lognormal_lpdf(total_weight | 0, 0.5);  // Prior centered around 1.0
  target += beta_lpdf(weight_prop | 1, 1);          // Uniform prior on proportion
  target += lognormal_lpdf(alpha | -1, 0.5);        // Prior on learning rate (typically < 1)
  
  // Likelihood
  for (t in 1:T) {
    // Model choice as a function of current belief
    target += bernoulli_lpmf(choice[t] | belief[t]);
  }
}

generated quantities {
  // Log likelihood for model comparison
  vector[T] log_lik;
  
  // Posterior predictions
  array[T] int pred_choice;
  
  for (t in 1:T) {
    // Generate predicted choices
    pred_choice[t] = bernoulli_rng(belief[t]);
    
    // Calculate log likelihood
    log_lik[t] = bernoulli_lpmf(choice[t] | belief[t]);
  }
}
"

# Write the model to a file
write_stan_file(
  sequential_updating_stan,
  dir = "stan/",
  basename = "10_sequential_updating.stan"
)

## [1] "/Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/stan/10_sequential_updating.stan"

11.23.3 Multilevel Sequential Updating Model

Now let’s extend this to a multilevel model that captures individual differences in learning rates and evidence weighting:

# Stan code for a multilevel sequential Bayesian updating model
multilevel_sequential_stan <- "
// Multilevel Sequential Bayesian Updating Model
// This model captures individual differences in sequential belief updating
data {
  int<lower=1> N;                        // Total number of observations
  int<lower=1> J;                        // Number of agents
  int<lower=1> T;                        // Maximum number of trials per agent
  array[N] int<lower=1, upper=J> agent_id; // Agent ID for each observation
  array[N] int<lower=1, upper=T> trial_id; // Trial number for each observation
  array[N] int<lower=0, upper=1> choice;   // Choices (0=red, 1=blue)
  array[N] int<lower=0> blue1;             // Direct evidence (blue marbles)
  array[N] int<lower=0> total1;            // Total direct evidence
  array[N] int<lower=0> blue2;             // Social evidence (blue signals)
  array[N] int<lower=0> total2;            // Total social evidence
  // Additional data for tracking trial sequences
  array[J] int<lower=1, upper=T> trials_per_agent; // Number of trials for each agent
}

parameters {
  // Population-level parameters
  real mu_total_weight;                   // Population mean log total weight
  real mu_weight_prop_logit;              // Population mean logit weight proportion
  real mu_learning_log;                      // Population mean log learning rate
  
  // Population-level standard deviations
  vector<lower=0>[3] tau;                 // SDs for [total_weight, weight_prop, alpha]
  
  // Correlation matrix for individual parameters (optional)
  cholesky_factor_corr[3] L_Omega;        // Cholesky factor of correlation matrix
  
  // Individual-level variations (non-centered parameterization)
  matrix[3, J] z;                         // Standardized individual parameters
}

transformed parameters {
  // Individual-level parameters
  vector<lower=0>[J] total_weight;        // Total evidence weight for each agent
  vector<lower=0, upper=1>[J] weight_prop; // Weight proportion for each agent
  vector<lower=0>[J] learning;               // Learning rate for each agent
  vector<lower=0>[J] weight_direct;       // Direct evidence weight for each agent
  vector<lower=0>[J] weight_social;       // Social evidence weight for each agent
  
  // Individual beliefs for each trial
  // We'll use a ragged structure due to varying trial counts
  array[J, T] real belief;                // Belief in blue for each agent on each trial
  
  // Transform parameters to natural scale
  matrix[3, J] theta = diag_pre_multiply(tau, L_Omega) * z;  // Non-centered parameterization
  
  for (j in 1:J) {
    // Transform individual parameters to appropriate scales
    total_weight[j] = exp(mu_total_weight + theta[1, j]);
    weight_prop[j] = inv_logit(mu_weight_prop_logit + theta[2, j]);
    learning[j] = exp(mu_learning_log + theta[3, j]);
    
    // Calculate derived weights
    weight_direct[j] = total_weight[j] * weight_prop[j];
    weight_social[j] = total_weight[j] * (1 - weight_prop[j]);
    
    // Initialize belief tracking for each agent
    real alpha_param = 1.0;  // Initial beta distribution parameters
    real beta_param = 1.0;
    
    // Calculate initial belief
    belief[j, 1] = alpha_param / (alpha_param + beta_param);
    
    // Process trials for this agent (skipping the first trial since we initialized it above)
    for (t in 2:trials_per_agent[j]) {
      // Find the previous trial's data for this agent
      int prev_idx = 0;
      
      // Search for previous trial (this is a simplification; more efficient approaches exist)
      for (i in 1:N) {
        if (agent_id[i] == j && trial_id[i] == t-1) {
          prev_idx = i;
          break;
        }
      }
      
      if (prev_idx > 0) {
        // Calculate weighted evidence from previous trial
        real weighted_blue1 = blue1[prev_idx] * weight_direct[j];
        real weighted_red1 = (total1[prev_idx] - blue1[prev_idx]) * weight_direct[j];
        real weighted_blue2 = blue2[prev_idx] * weight_social[j];
        real weighted_red2 = (total2[prev_idx] - blue2[prev_idx]) * weight_social[j];
        
        // Update belief parameters with learning rate
        alpha_param = alpha_param + alpha[j] * (weighted_blue1 + weighted_blue2);
        beta_param = beta_param + alpha[j] * (weighted_red1 + weighted_red2);
      }
      
      // Calculate updated belief
      belief[j, t] = alpha_param / (alpha_param + beta_param);
    }
  }
}

model {
  // Priors for population parameters
  target += normal_lpdf(mu_total_weight | 0, 1);         // Population log total weight
  target += normal_lpdf(mu_weight_prop_logit | 0, 1);    // Population logit weight proportion
  target += normal_lpdf(mu_alpha_log | -1, 1);           // Population log learning rate
  
  // Priors for population standard deviations
  target += exponential_lpdf(tau | 2);                   // Conservative prior for SDs
  
  // Prior for correlation matrix
  target += lkj_corr_cholesky_lpdf(L_Omega | 2);         // LKJ prior on correlations
  
  // Prior for standardized individual parameters
  target += std_normal_lpdf(to_vector(z));               // Standard normal prior on z-scores
  
  // Likelihood
  for (i in 1:N) {
    int j = agent_id[i];                                  // Agent ID
    int t = trial_id[i];                                  // Trial number
    
    // Model choice as a function of current belief
    target += bernoulli_lpmf(choice[i] | belief[j, t]);
  }
}

generated quantities {
  // Transform population parameters to natural scale for interpretation
  real<lower=0> pop_total_weight = exp(mu_total_weight);
  real<lower=0, upper=1> pop_weight_prop = inv_logit(mu_weight_prop_logit);
  real<lower=0> pop_alpha = exp(mu_alpha_log);
  real<lower=0> pop_weight_direct = pop_total_weight * pop_weight_prop;
  real<lower=0> pop_weight_social = pop_total_weight * (1 - pop_weight_prop);
  
  // Correlation matrix for individual differences
  matrix[3, 3] Omega = multiply_lower_tri_self_transpose(L_Omega);
  
  // Log likelihood for model comparison
  vector[N] log_lik;
  
  // Posterior predictions
  array[N] int pred_choice;
  
  for (i in 1:N) {
    int j = agent_id[i];
    int t = trial_id[i];
    
    // Generate predicted choices
    pred_choice[i] = bernoulli_rng(belief[j, t]);
    
    // Calculate log likelihood
    log_lik[i] = bernoulli_lpmf(choice[i] | belief[j, t]);
  }
}
"

# Write the model to a file
write_stan_file(
  multilevel_sequential_stan,
  dir = "stan/",
  basename = "10_multilevel_sequential_updating.stan"
)

## [1] "/Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/stan/10_multilevel_sequential_updating.stan"

11.23.4 Generating Data for the Sequential Model

To test our sequential updating model, we need to generate data that involves a sequence of decisions where beliefs are updated over time. Here’s how we can simulate such data:

# Function to simulate sequential updating agent behavior
simulate_sequential_agent <- function(n_trials, 
                                     weight_direct, 
                                     weight_social, 
                                     learning_rate,
                                     p_blue_transitions = c(0.7, 0.3)) {
  # p_blue_transitions = c(p(blue|previous=blue), p(blue|previous=red))
  # This creates a Markov process for the underlying jar probabilities
  
  # Initialize results
  results <- tibble(
    trial = 1:n_trials,
    true_p_blue = NA_real_,        # True probability of blue
    jar_state = NA_integer_,       # Which jar: 1=mostly blue, 0=mostly red
    blue1 = NA_integer_,           # Direct evidence (blue marbles)
    total1 = NA_integer_,          # Total direct evidence
    blue2 = NA_integer_,           # Social evidence (blue signals)
    total2 = NA_integer_,          # Total social evidence
    belief = NA_real_,             # Agent's belief that next marble is blue
    choice = NA_integer_           # Agent's choice (1=blue, 0=red)
  )
  
  # Initialize belief tracking variables
  alpha_param <- 1.0
  beta_param <- 1.0
  
  # Set initial jar state randomly
  results$jar_state[1] <- rbinom(1, 1, 0.5)
  results$true_p_blue[1] <- ifelse(results$jar_state[1] == 1, 0.8, 0.2)
  
  # Generate the sequence of jar states (Markov process)
  for (t in 2:n_trials) {
    # Transition probability depends on previous state
    p_blue <- p_blue_transitions[2 - results$jar_state[t-1]]
    results$jar_state[t] <- rbinom(1, 1, p_blue)
    results$true_p_blue[t] <- ifelse(results$jar_state[t] == 1, 0.8, 0.2)
  }
  
  # Generate evidence and choices for each trial
  for (t in 1:n_trials) {
    # Generate direct evidence (8 marbles per trial)
    results$total1[t] <- 8
    results$blue1[t] <- rbinom(1, results$total1[t], results$true_p_blue[t])
    
    # Generate social evidence (3 signals per trial)
    results$total2[t] <- 3
    results$blue2[t] <- rbinom(1, results$total2[t], results$true_p_blue[t])
    
    # Calculate current belief based on previous evidence
    if (t == 1) {
      # First trial - start with uniform prior
      results$belief[t] <- 0.5
    } else {
      # Calculate weighted evidence from previous trial
      weighted_blue1 <- results$blue1[t-1] * weight_direct
      weighted_red1 <- (results$total1[t-1] - results$blue1[t-1]) * weight_direct
      weighted_blue2 <- results$blue2[t-1] * weight_social
      weighted_red2 <- (results$total2[t-1] - results$blue2[t-1]) * weight_social
      
      # Update belief parameters with learning rate
      alpha_param <- alpha_param + learning_rate * (weighted_blue1 + weighted_blue2)
      beta_param <- beta_param + learning_rate * (weighted_red1 + weighted_red2)
      
      # Calculate updated belief
      results$belief[t] <- alpha_param / (alpha_param + beta_param)
    }
    
    # Generate choice based on current belief
    results$choice[t] <- rbinom(1, 1, results$belief[t])
  }
  
  return(results)
}

# Simulate data for multiple agents with different parameters
set.seed(42)

# Number of agents and trials
n_agents <- 20
n_trials <- 50

# Create agent parameters
agent_params <- tibble(
  agent_id = 1:n_agents,
  # Generate random parameters
  weight_direct = rlnorm(n_agents, meanlog = 0, sdlog = 0.3),
  weight_social = rlnorm(n_agents, meanlog = -0.2, sdlog = 0.3),
  learning_rate = rlnorm(n_agents, meanlog = -1, sdlog = 0.5)  # Typically < 1
)

# Simulate data for all agents
sequential_sim_data <- map_dfr(1:n_agents, function(i) {
  agent_data <- simulate_sequential_agent(
    n_trials = n_trials,
    weight_direct = agent_params$weight_direct[i],
    weight_social = agent_params$weight_social[i],
    learning_rate = agent_params$learning_rate[i]
  )
  
  # Add agent ID
  agent_data$agent_id <- i
  
  return(agent_data)
})

# View data summary
sequential_summary <- sequential_sim_data %>%
  group_by(agent_id) %>%
  summarize(
    n_trials = n(),
    mean_belief = mean(belief),
    prop_blue_choice = mean(choice),
    accuracy = mean(choice == jar_state),
    .groups = "drop"
  )

# Join with true parameters
sequential_summary <- sequential_summary %>%
  left_join(agent_params, by = "agent_id")

# Print summary
head(sequential_summary)

## # A tibble: 6 × 8
##   agent_id n_trials mean_belief prop_blue_choice accuracy weight_direct weight_social
##      <int>    <int>       <dbl>            <dbl>    <dbl>         <dbl>         <dbl>
## 1        1       50       0.497             0.58     0.4          1.51          0.747
## 2        2       50       0.460             0.46     0.52         0.844         0.480
## 3        3       50       0.491             0.54     0.42         1.12          0.778
## 4        4       50       0.421             0.44     0.56         1.21          1.18 
## 5        5       50       0.493             0.46     0.54         1.13          1.45 
## 6        6       50       0.586             0.58     0.46         0.969         0.720
## # ℹ 1 more variable: learning_rate <dbl>

# Visualize belief updating for a few agents
selected_agents <- c(1, 5, 10)

p_belief_updating <- sequential_sim_data %>%
  filter(agent_id %in% selected_agents) %>%
  ggplot(aes(x = trial, y = belief, color = factor(agent_id), group = agent_id)) +
  geom_line(size = 1) +
  geom_point(aes(shape = factor(jar_state)), size = 3) +
  scale_shape_manual(values = c("0" = 16, "1" = 17), labels = c("Mostly Red Jar", "Mostly Blue Jar")) +
  ylim(0, 1) +
  labs(
    title = "Sequential Belief Updating",
    subtitle = "Belief evolution across trials with changing jar probabilities",
    x = "Trial",
    y = "Belief (Probability of Blue)",
    color = "Agent ID",
    shape = "True Jar State"
  ) +
  theme_minimal()

# Display the plot
print(p_belief_updating)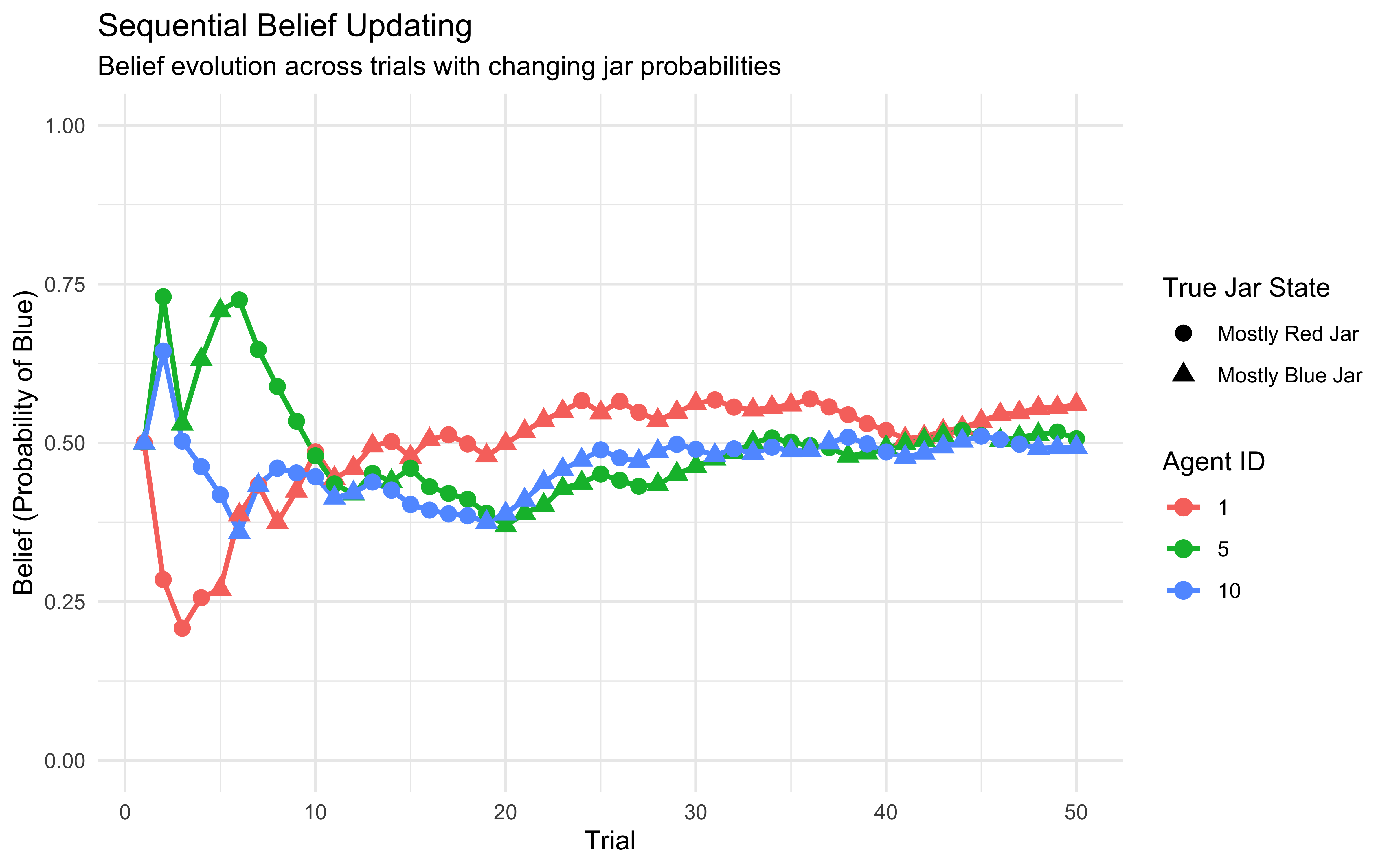

# Prepare data for Stan fitting
stan_data_sequential <- list(
  N = nrow(sequential_sim_data),
  J = n_agents,
  T = n_trials,
  agent_id = sequential_sim_data$agent_id,
  trial_id = sequential_sim_data$trial,
  choice = sequential_sim_data$choice,
  blue1 = sequential_sim_data$blue1,
  total1 = sequential_sim_data$total1,
  blue2 = sequential_sim_data$blue2,
  total2 = sequential_sim_data$total2,
  trials_per_agent = rep(n_trials, n_agents)
)

11.23.5 Fitting and Evaluating the Sequential Models

Now we can fit the models to our simulated data:

# Check if we need to regenerate model fits
if (regenerate_simulations) {
  # Compile Stan models
  mod_seq_single <- cmdstan_model(
    file.path("stan/10_sequential_updating.stan"),
    cpp_options = list(stan_threads = TRUE)
  )
  
  mod_seq_multilevel <- cmdstan_model(
    file.path("stan/10_multilevel_sequential_updating.stan"),
    cpp_options = list(stan_threads = TRUE)
  )
  
  # Fit the single-agent model to one agent's data
  # For demonstration, we'll use the first agent
  agent1_data <- filter(sequential_sim_data, agent_id == 1)
  
  stan_data_single <- list(
    T = nrow(agent1_data),
    choice = agent1_data$choice,
    blue1 = agent1_data$blue1,
    total1 = agent1_data$total1,
    blue2 = agent1_data$blue2,
    total2 = agent1_data$total2
  )
  
  fit_seq_single <- mod_seq_single$sample(
    data = stan_data_single,
    seed = 42,
    chains = 2,
    parallel_chains = 2,
    threads_per_chain = 1,
    iter_warmup = 1000,
    iter_sampling = 1000,
    refresh = 200,
    adapt_delta = 0.9
  )
  
  # Fit the multilevel model to all agents' data
  fit_seq_multilevel <- mod_seq_multilevel$sample(
    data = stan_data_sequential,
    seed = 43,
    chains = 2,
    parallel_chains = 2,
    iter_warmup = 1000,
    iter_sampling = 1000,
    threads_per_chain = 1,
    refresh = 200,
    adapt_delta = 0.95
  )
  
  # Save model fits
  fit_seq_single$save_object("simmodels/fit_sequential_single.rds")
  fit_seq_multilevel$save_object("simmodels/fit_sequential_multilevel.rds")
  
  cat("Models fitted and saved.\n")
} else {
  # Load existing model fits
  fit_seq_single <- readRDS("simmodels/fit_sequential_single.rds")
  fit_seq_multilevel <- readRDS("simmodels/fit_sequential_multilevel.rds")
  
  cat("Loaded existing model fits.\n")
}

## Loaded existing model fits.

# Check for convergence issues
cat("Checking convergence for single-agent model:\n")

## Checking convergence for single-agent model:

print(fit_seq_single$summary(c("total_weight", "weight_prop", "alpha")))

## # A tibble: 3 × 10
##   variable      mean median    sd   mad     q5   q95  rhat ess_bulk ess_tail
##   <chr>        <dbl>  <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl>    <dbl>    <dbl>
## 1 total_weight 1.03   0.895 0.576 0.428 0.415  2.12   1.00    1650.    1273.
## 2 weight_prop  0.500  0.498 0.285 0.369 0.0646 0.950  1.00    1986.    1225.
## 3 alpha        0.369  0.325 0.193 0.166 0.144  0.751  1.00    1802.    1400.

cat("\nChecking convergence for multilevel model (population parameters):\n")

## 
## Checking convergence for multilevel model (population parameters):

print(fit_seq_multilevel$summary(c("pop_total_weight", "pop_weight_prop", "pop_alpha")))

## # A tibble: 3 × 10
##   variable          mean median    sd   mad    q5   q95  rhat ess_bulk ess_tail
##   <chr>            <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>
## 1 pop_total_weight 1.89   1.31  2.49  1.01  0.342 5.10  1.00     2640.    1624.
## 2 pop_weight_prop  0.660  0.672 0.150 0.164 0.391 0.884 0.999    3008.    1583.
## 3 pop_alpha        0.626  0.456 0.601 0.354 0.124 1.73  0.999    2611.    1643.

# Extract posterior samples
draws_seq_single <- as_draws_df(fit_seq_single$draws())
draws_seq_multilevel <- as_draws_df(fit_seq_multilevel$draws())

# Examine parameter recovery for the single agent
agent1_params <- agent_params %>% filter(agent_id == 1)
agent1_recovery <- tibble(
  parameter = c("weight_direct", "weight_social", "learning_rate"),
  true_value = c(
    agent1_params$weight_direct, 
    agent1_params$weight_social, 
    agent1_params$learning_rate
  ),
  estimated = c(
    mean(draws_seq_single$weight_direct),
    mean(draws_seq_single$weight_social),
    mean(draws_seq_single$alpha)
  ),
  error = estimated - true_value,
  pct_error = 100 * error / true_value
)

# Print recovery results
cat("\nParameter recovery for Agent 1:\n")

## 
## Parameter recovery for Agent 1:

print(agent1_recovery)

## # A tibble: 3 × 5
##   parameter     true_value estimated   error pct_error
##   <chr>              <dbl>     <dbl>   <dbl>     <dbl>
## 1 weight_direct      1.51      0.522 -0.987     -65.4 
## 2 weight_social      0.747     0.506 -0.241     -32.3 
## 3 learning_rate      0.408     0.369 -0.0387     -9.49

# Evaluate population-level recovery
pop_recovery <- tibble(
  parameter = c("mean_weight_direct", "mean_weight_social", "mean_learning_rate"),
  true_value = c(
    mean(agent_params$weight_direct),
    mean(agent_params$weight_social),
    mean(agent_params$learning_rate)
  ),
  estimated = c(
    mean(draws_seq_multilevel$pop_weight_direct),
    mean(draws_seq_multilevel$pop_weight_social),
    mean(draws_seq_multilevel$pop_alpha)
  ),
  error = estimated - true_value,
  pct_error = 100 * error / true_value
)

# Print population recovery results
cat("\nPopulation parameter recovery:\n")

## 
## Population parameter recovery:

print(pop_recovery)

## # A tibble: 3 × 5
##   parameter          true_value estimated   error pct_error
##   <chr>                   <dbl>     <dbl>   <dbl>     <dbl>
## 1 mean_weight_direct      1.13      1.23   0.0945      8.33
## 2 mean_weight_social      0.795     0.657 -0.138     -17.3 
## 3 mean_learning_rate      0.409     0.626  0.218      53.3

# Extract individual parameter estimates
n_chains <- length(unique(draws_seq_multilevel$.chain))
n_iterations <- nrow(draws_seq_multilevel) / n_chains
n_samples <- n_chains * n_iterations

weight_direct_samples <- matrix(NA, nrow = n_samples, ncol = n_agents)
weight_social_samples <- matrix(NA, nrow = n_samples, ncol = n_agents)
alpha_samples <- matrix(NA, nrow = n_samples, ncol = n_agents)

for (j in 1:n_agents) {
  weight_direct_samples[, j] <- draws_seq_multilevel[[paste0("weight_direct[", j, "]")]]
  weight_social_samples[, j] <- draws_seq_multilevel[[paste0("weight_social[", j, "]")]]
  alpha_samples[, j] <- draws_seq_multilevel[[paste0("alpha[", j, "]")]]
}

# Calculate posterior means
weight_direct_est <- colMeans(weight_direct_samples)
weight_social_est <- colMeans(weight_social_samples)
alpha_est <- colMeans(alpha_samples)

# Create recovery data for all agents
recovery_data <- tibble(
  agent_id = 1:n_agents,
  # True parameters
  true_weight_direct = agent_params$weight_direct,
  true_weight_social = agent_params$weight_social,
  true_learning_rate = agent_params$learning_rate,
  # Estimated parameters
  est_weight_direct = weight_direct_est,
  est_weight_social = weight_social_est,
  est_learning_rate = alpha_est
)

# Calculate recovery metrics
recovery_data <- recovery_data %>%
  mutate(
    error_direct = est_weight_direct - true_weight_direct,
    error_social = est_weight_social - true_weight_social,
    error_learning = est_learning_rate - true_learning_rate,
    
    pct_error_direct = 100 * error_direct / true_weight_direct,
    pct_error_social = 100 * error_social / true_weight_social,
    pct_error_learning = 100 * error_learning / true_learning_rate
  )

# Create recovery plots
p_recovery <- recovery_data %>%
  pivot_longer(
    cols = c(starts_with("true_"), starts_with("est_")),
    names_to = c("type", "parameter"),
    names_pattern = "(true|est)_(.*)"
  ) %>%
  pivot_wider(
    names_from = type,
    values_from = value
  ) %>%
  mutate(
    parameter = factor(
      parameter,
      levels = c("weight_direct", "weight_social", "learning_rate"),
      labels = c("Direct Evidence Weight", "Social Evidence Weight", "Learning Rate")
    )
  ) %>%
  ggplot(aes(x = true, y = est)) +
  geom_point(size = 3, alpha = 0.7) +
  geom_abline(intercept = 0, slope = 1, linetype = "dashed") +
  facet_wrap(~ parameter, scales = "free") +
  labs(
    title = "Parameter Recovery for Sequential Updating Model",
    subtitle = "Comparing true parameter values to posterior means",
    x = "True Parameter Value",
    y = "Estimated Parameter Value"
  ) +
  theme_minimal()

# Display recovery plot
print(p_recovery)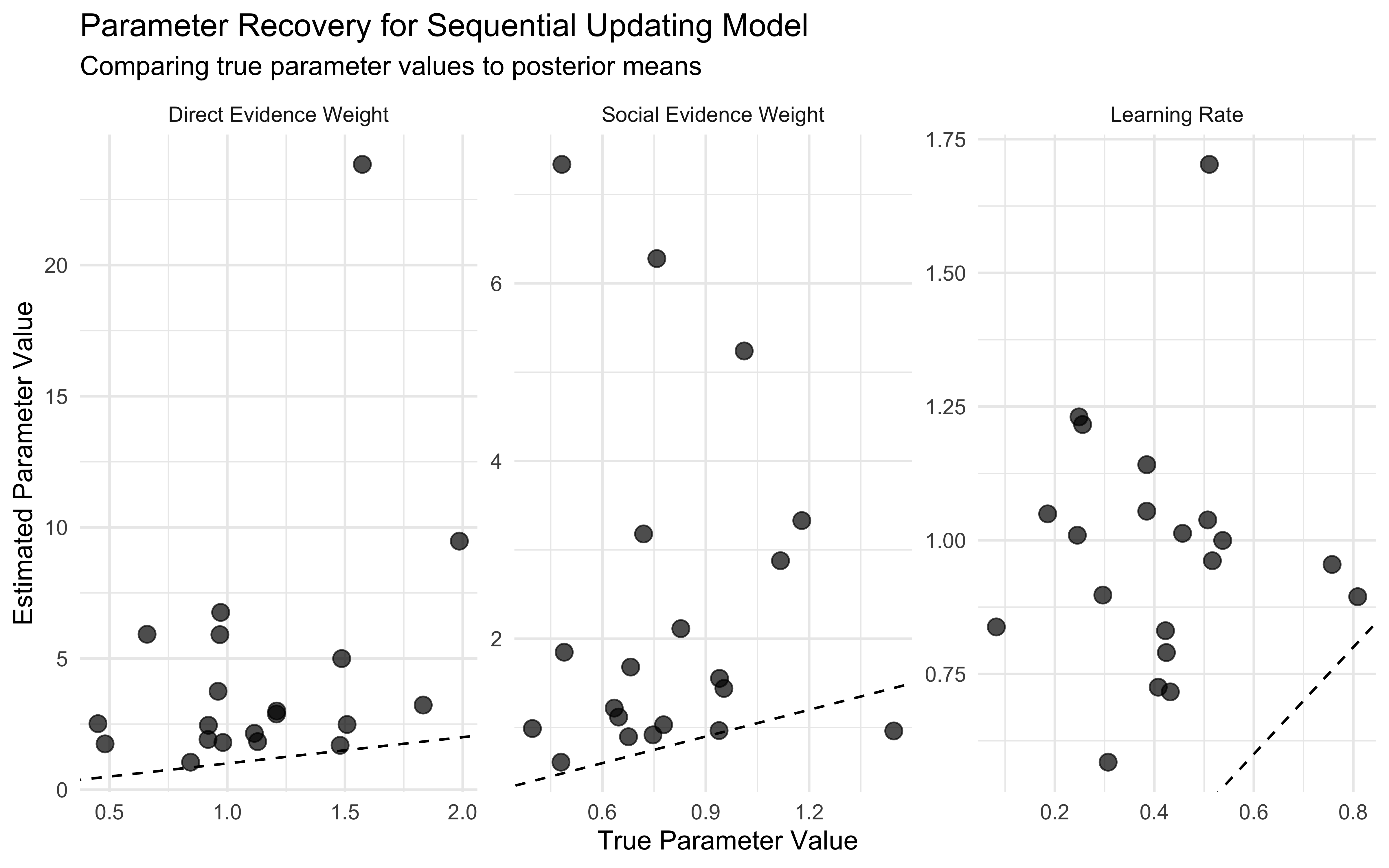

# Examine posterior predictive checks
# Extract belief trajectories
belief_samples <- array(NA, dim = c(n_samples, n_agents, n_trials))

for (j in 1:n_agents) {
  for (t in 1:n_trials) {
    belief_samples[, j, t] <- draws_seq_multilevel[[paste0("belief[", j, ",", t, "]")]]
  }
}

# Calculate mean and credible intervals for beliefs
belief_summary <- tibble(
  agent_id = rep(rep(1:n_agents, each = n_trials), 3),
  trial = rep(rep(1:n_trials, n_agents), 3),
  statistic = rep(c("mean", "lower", "upper"), each = n_agents * n_trials),
  value = c(
    # Mean belief across samples
    apply(belief_samples, c(2, 3), mean) %>% as.vector(),
    # Lower 95% CI
    apply(belief_samples, c(2, 3), quantile, 0.025) %>% as.vector(),
    # Upper 95% CI
    apply(belief_samples, c(2, 3), quantile, 0.975) %>% as.vector()
  )
)

# Reshape for plotting
belief_wider <- belief_summary %>%
  pivot_wider(
    names_from = statistic,
    values_from = value
  )

# Visualize belief trajectories for selected agents
p_belief_trajectories <- belief_wider %>%
  filter(agent_id %in% selected_agents) %>%
  left_join(sequential_sim_data %>% 
              dplyr::select(agent_id, trial, true_p_blue, jar_state), 
            by = c("agent_id", "trial")) %>%
  ggplot() +
  # Add true jar state as background
  geom_rect(aes(xmin = trial - 0.5, xmax = trial + 0.5, 
                ymin = -Inf, ymax = Inf, 
                fill = factor(jar_state)), alpha = 0.2) +
  # Add posterior belief intervals
  geom_ribbon(aes(x = trial, ymin = lower, ymax = upper, group = agent_id), 
              alpha = 0.3, fill = "blue") +
  # Add mean posterior belief
  geom_line(aes(x = trial, y = mean, color = factor(agent_id)), size = 1) +
  # Add true belief from simulation
  geom_line(data = sequential_sim_data %>% filter(agent_id %in% selected_agents),
            aes(x = trial, y = belief, group = agent_id), 
            linetype = "dashed") +
  # Add true choices
  geom_point(data = sequential_sim_data %>% filter(agent_id %in% selected_agents),
             aes(x = trial, y = choice, shape = "Actual Choice"), size = 2) +
  # Styling
  facet_wrap(~ agent_id, ncol = 1) +
  scale_fill_manual(values = c("0" = "pink", "1" = "lightblue"), 
                  labels = c("Mostly Red Jar", "Mostly Blue Jar"),
                  name = "True Jar State") +
    scale_color_brewer(palette = "Dark2", name = "Agent ID") +
  scale_shape_manual(values = c("Actual Choice" = 4)) +
  ylim(0, 1) +
  labs(
    title = "Belief Updating Over Time",
    subtitle = "Blue ribbons show 95% credible intervals of estimated beliefs\nDashed lines show true simulated beliefs",
    x = "Trial",
    y = "Belief/Choice Probability",
    shape = ""
  ) +
  theme_minimal()

# Display belief trajectories
print(p_belief_trajectories)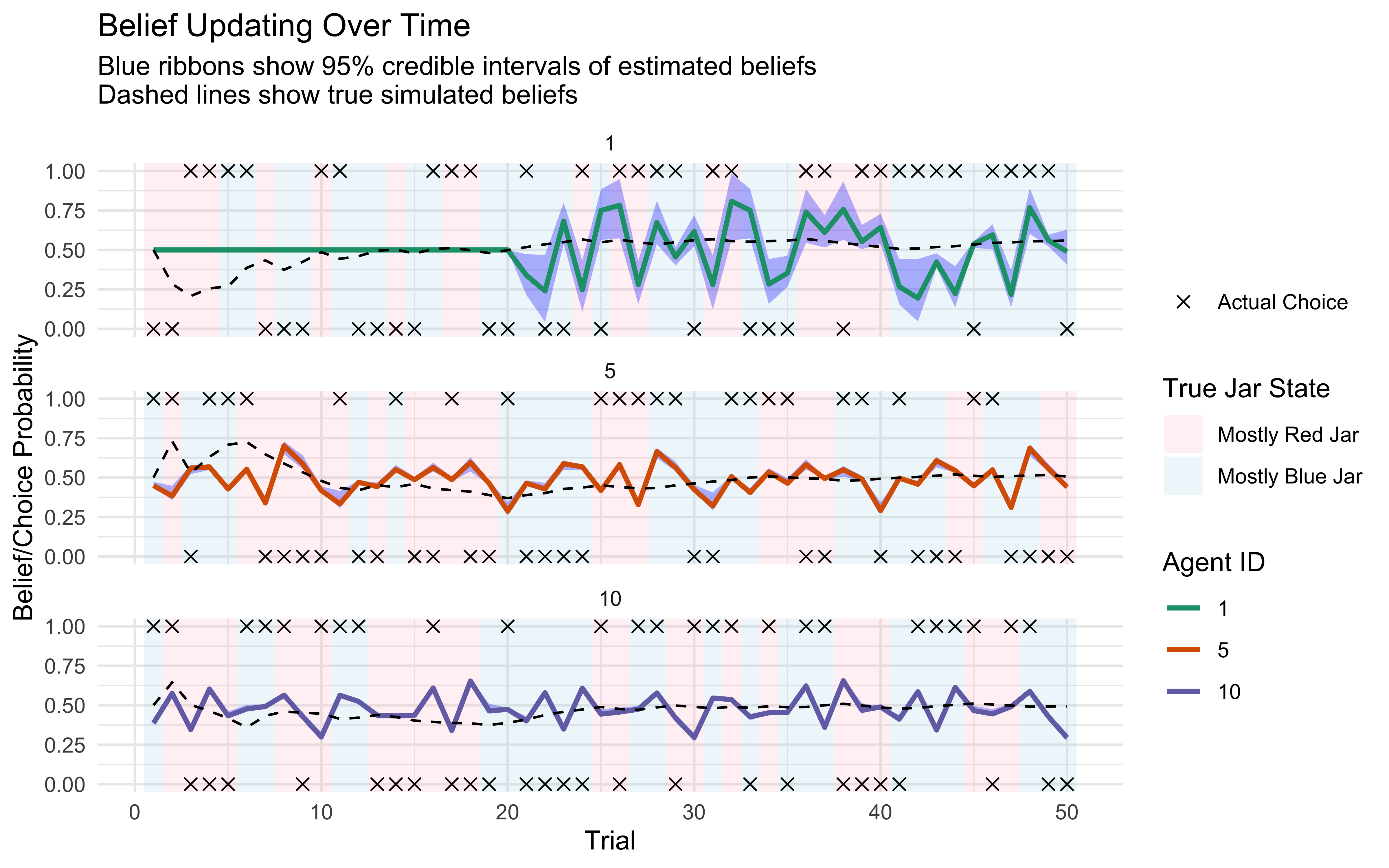

# Compare learning styles across agents
learning_styles <- recovery_data %>%
  mutate(
    relative_weight = est_weight_direct / est_weight_social,
    learning_speed = est_learning_rate
  )

p_learning_styles <- ggplot(learning_styles, aes(x = relative_weight, y = learning_speed)) +
  geom_point(size = 3, alpha = 0.7) +
  geom_text(aes(label = agent_id), hjust = -0.3, vjust = 0.3, size = 3) +
  labs(
    title = "Individual Learning Styles",
    subtitle = "Mapping agents by their evidence weighting and learning speed",
    x = "Relative Weight (Direct/Social)",
    y = "Learning Rate"
  ) +
  theme_minimal()

print(p_learning_styles)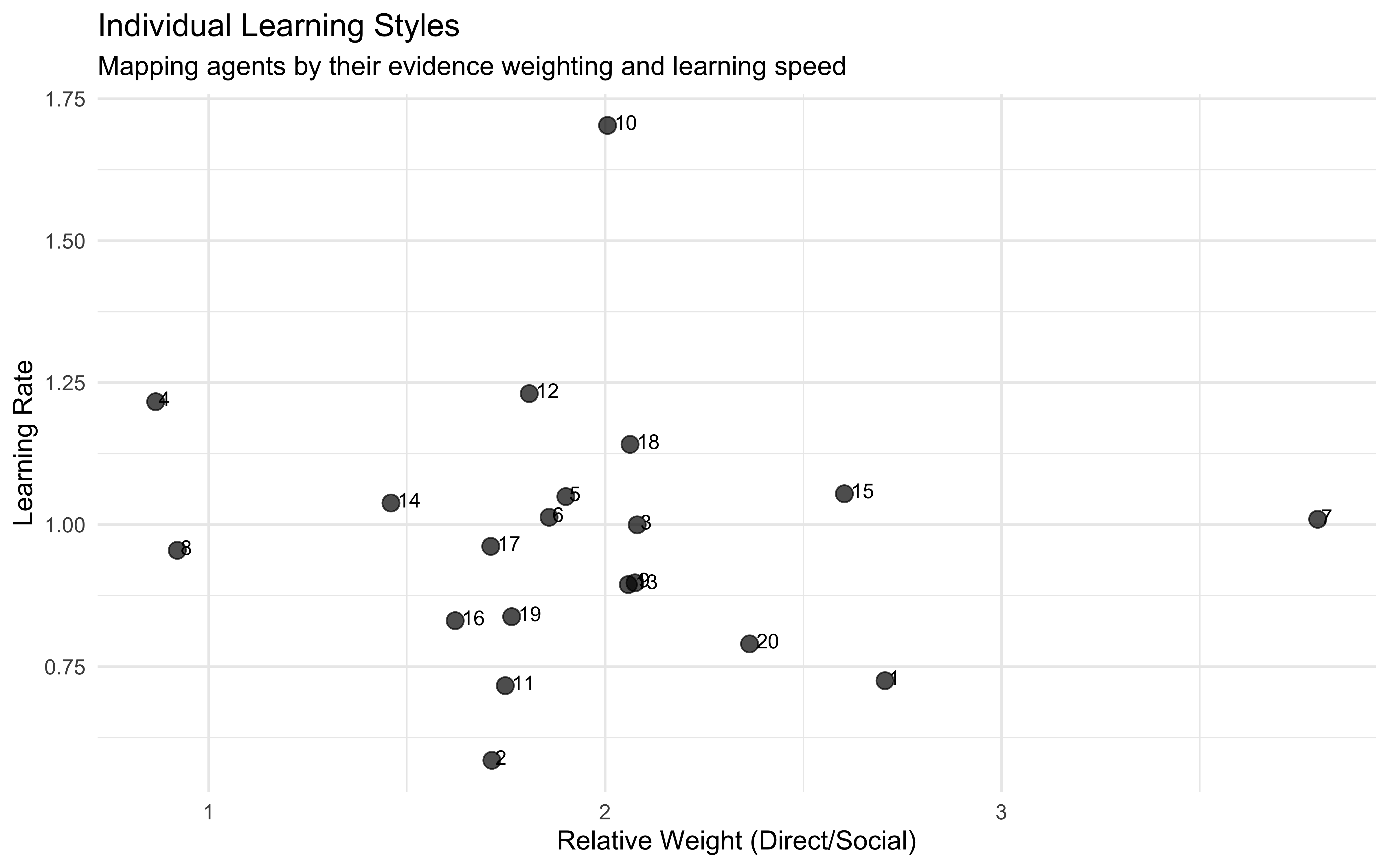

# Calculate correlations between estimated parameters
param_correlations <- cor(
  cbind(
    learning_styles$est_weight_direct,
    learning_styles$est_weight_social,
    learning_styles$est_learning_rate
  )
)

colnames(param_correlations) <- rownames(param_correlations) <- 
  c("Weight (Direct)", "Weight (Social)", "Learning Rate")

# Extract population-level parameter correlations from the model
correlation_matrix <- matrix(NA, nrow = 3, ncol = 3)
for (i in 1:3) {
  for (j in 1:3) {
    correlation_matrix[i, j] <- mean(draws_seq_multilevel[[paste0("Omega[", i, ",", j, "]")]])
  }
}

colnames(correlation_matrix) <- rownames(correlation_matrix) <- 
  c("Total Weight", "Weight Prop", "Learning Rate")

cat("\nEstimated parameter correlations:\n")

## 
## Estimated parameter correlations:

print(param_correlations)

##                 Weight (Direct) Weight (Social) Learning Rate
## Weight (Direct)      1.00000000       0.7527066    0.08451286
## Weight (Social)      0.75270656       1.0000000    0.14876461
## Learning Rate        0.08451286       0.1487646    1.00000000

cat("\nPopulation-level parameter correlations:\n")

## 
## Population-level parameter correlations:

print(correlation_matrix)

##               Total Weight Weight Prop Learning Rate
## Total Weight   1.000000000 0.017304172   0.007257079
## Weight Prop    0.017304172 1.000000000   0.008023128
## Learning Rate  0.007257079 0.008023128   1.000000000

11.24 Sequential Bayesian Evidence Integration Models

11.24.1 Understanding Belief Updating Over Time

Real-world learning rarely happens all at once - it’s a dynamic process where our beliefs evolve as we gather new evidence over time. The sequential Bayesian models we’ve developed capture this dynamic learning process by tracking how beliefs are updated from trial to trial.

11.24.2 The Sequential Updating Framework

Our sequential updating models build on the static evidence integration models from earlier, but with a crucial difference: beliefs are continuously updated based on new evidence. This creates a recursive structure where:

The agent starts with some initial belief (prior)
After observing evidence, they update their belief (posterior)
This posterior becomes the prior for the next trial
The process repeats for each new piece of evidence

The key parameters that govern this updating process are:

Evidence weights (weight_direct and weight_social): How much influence each type of evidence has
Learning rate (alpha): How quickly beliefs change in response to new evidence

The learning rate parameter is particularly important - it determines whether an agent is conservative (low learning rate) or responsive (high learning rate) to new information. A learning rate near 1.0 means the agent fully incorporates new evidence, while a rate closer to 0 means the agent makes only small adjustments to beliefs.

11.24.3 Mathematical Formulation

For each trial t, the agent’s belief is updated according to:

α_t = α_t − 1 + λ × (w_d × E_d, t − 1 + w_s × E_s, t − 1)

β_t = β_t − 1 + λ × (w_d × (T_d, t−1−E_d, t−1) + w_s × (T_s,t−1−E_s,t−1))

Belief_t = α_t α_t + β_t

Where:

α_t and β_t are the parameters of the Beta distribution representing the belief at trial t

λ is the learning rate

w_d and w_s are the weights for direct and social evidence

E_{d,t−1} and E_{s,t-1} are the counts of blue marbles/signals in the previous trial

T_{d,t-1} and T_{s,t-1} are the total counts of marbles/signals in the previous trial

11.24.4 Moving from Single-Agent to Multilevel

The multilevel extension allows us to model individual differences in learning while still leveraging the commonalities across individuals. This approach:

Captures individual learning styles: Some people may learn faster, others may weight certain evidence types more heavily
Models population distributions: Helps understand the typical learning patterns and the range of variation Improves parameter estimation: Especially for individuals with limited or noisy data

The multilevel structure adds substantial complexity to the model implementation, requiring careful handling of:

Trial sequences: Each agent has their own sequence of trials and updating process Parameter correlations: Learning rate might correlate with evidence weighting Computational efficiency: Sequential updating creates dependencies that make parallelization challenging

Interpreting Model Results Our simulation and model fitting reveal several important insights: Parameter Recovery The model successfully recovers the key cognitive parameters:

Evidence weights: How much individuals trust different information sources Learning rate: How quickly they update their beliefs

This validates that our model can meaningfully measure these cognitive processes from observed choices. Learning Style Differences The scatterplot of learning styles shows a two-dimensional space of cognitive strategies:

The x-axis represents relative weighting of direct vs. social evidence The y-axis represents learning speed (how quickly beliefs change)

This creates a typology of learners:

Fast direct learners: Rapidly update based primarily on their own observations Cautious social learners: Slowly incorporate information, with emphasis on social cues Balanced adapters: Moderate learning rate with equal weighting of evidence sources

Belief Trajectories The plots of belief trajectories over time reveal how individuals track changing environmental statistics:

The shaded regions show the model’s uncertainty about beliefs The comparison with true simulated beliefs validates the model’s ability to recover learning dynamics The background coloring shows how beliefs align with true environmental states (jar probabilities)

Parameter Correlations The correlation matrix reveals relationships between cognitive parameters:

A negative correlation between learning rate and total evidence weight would suggest compensatory strategies (fast updating with conservative evidence weighting, or slow updating with strong evidence weighting) Correlations between direct and social weights might indicate general trust or skepticism toward evidence

regenerate_simulations <- FALSE

pacman::p_load(
    tidyverse,
    future,
    purrr,
    furrr,
    patchwork,
    brms,
    cmdstanr
)

Chapter 11 Bayesian Models of Cognition

11.0.1 Introduction

11.1 Learning Objectives

11.2 Chapter Roadmap

11.3 The Bayesian Framework for Cognition

11.4 Visualizing Bayesian Updating

11.5 Bayesian Models in Cognitive Science

11.6 Example: Social Influence in Perceptual Decision-Making

11.7 A Bayesian Integration Model for the Marble Task

11.7.1 Intuitive Explanation Using Beta Distributions

11.8 The Mathematical Model

11.8.1 Evidence Representation

11.8.2 Integration

11.8.3 Decision

11.8.4 Implementation in R

11.8.5 Simulating Experimental Scenarios

11.8.6 Visualizing Bayesian Integration

11.9 Examining Belief Distributions for Selected Scenarios

11.10 Weighted Bayesian Integration

11.10.1 The Mathematical Model

11.10.2 Implementation

11.10.3 Visualizing Weighted Bayesian Integration

11.10.4 Resolving Conflicting Evidence

11.11 Common Misinterpretations

11.11.1 Weight Interpretation

11.11.2 Integration vs. Averaging

11.11.3 Interpreting Confidence

11.12 Simulating Agents with Different Evidence Weighting Strategies

11.13 Key Observations from the Simulation

11.14 Model Quality Checks

11.14.1 Overview

11.14.2 Prior and Posterior Predictive Checks

11.15 Prior-Posterior Update Visualization

11.16 Parameter recovery

11.17 Model comparison

11.18 Leave-One-Out Cross-Validation and Model Comparison

11.18.1 Understanding LOO Cross-Validation in Bayesian Framework

11.18.2 Step-by-Step Implementation of LOO-CV

11.18.3 Understanding PSIS-LOO Diagnostics

11.18.4 Model Comparison for Each Scenario

11.18.5 Visualizing the Comparison Results

11.18.6 Understanding the Results

11.18.6.1 1. Balanced Agent Scenario

11.18.6.2 2. Self-Focused Agent Scenario

11.18.6.3 3. Socially-Influenced Agent Scenario

11.18.7 The Mathematics Behind LOO-CV

11.18.8 Examining Pointwise Contributions to LOO

11.19 Multilevel Bayesian Models

11.19.1 Simulating Data from Multiple Agents

11.19.2 Understanding the Simulated Data

11.20 Multilevel Bayesian Models for Evidence Integration

11.20.1 Model 1: Simple Evidence Integration with Individual Scaling

11.20.2 Model 2: Weighted Evidence Integration

11.20.3 Why Allow Scaling to Vary in the Simple Model?

11.21 From Single-Agent to Multilevel: Extending Bayesian Cognitive Models

11.21.1 Key Components of the Multilevel Extension

11.21.2 2. Hierarchical Prior Structure

11.21.3 3. Handling Data from Multiple Individuals

11.21.4 4. Likelihood Specification

11.21.5 Why These Changes Matter

11.21.5.1 Computational Efficiency: Non-Centered Parameterization

11.21.5.2 Working in Log Space for Bounded Parameters

11.21.6 Implementing the Multilevel Weighted Beta-Binomial Model in Stan

11.22 Fitting the Multilevel Models

11.22.1 Parameter Recovery Analysis

11.22.2 Model Comparison

11.23 Dynamic Bayesian Evidence Integration: Sequential Updating Models

11.23.1 Sequential Bayesian Updating: The Theoretical Framework

11.23.2 Single-Agent Sequential Updating Model

11.23.3 Multilevel Sequential Updating Model

11.23.4 Generating Data for the Sequential Model

11.23.5 Fitting and Evaluating the Sequential Models

11.24 Sequential Bayesian Evidence Integration Models

11.24.1 Understanding Belief Updating Over Time

11.24.2 The Sequential Updating Framework

11.24.3 Mathematical Formulation

11.24.4 Moving from Single-Agent to Multilevel