Chapter 8 Bonus chapter: Additional models developed by students
8.1 Additional models
Additional models that have been developed by previous students:
8.1.3 Memory agent with exponential memory decay (rate)
Memory = alpha * memory + (1 - alpha) * otherChoice
8.1.4 Memory agent with exponential memory decay (exponential)
The agent uses a weighted memory store, where previous choices are weighted by a factor based on how far back in the past they were made, represented by power. The agent first creates a vector of weights for each of the previous choices based on their position in the memory store and the power value. This model implements exponential decay of memory, according to a power law. Specifically, the opposing agent’s choices up to the present trial are encoded as 1’s and -1’s. The choices are weighted, and then summed. So, on trial i, the memory of the previous trial j is given a weight corresponding to j^(-1). Higher values of j correspond to earlier trials, with j = 1 being the most recent. Then a choice is made based on this weight according to the following formula:
Theta = inv_logit(alpha + beta * weightedMemory)
[N.B. really poor parameter recovery]
8.1.5 Memory agent with exponential memory decay, but separate memory for wins and losses
[N.B. really poor parameter recovery]
8.4 Generate data
[MISSING: EXPLAIN THE MODEL STEP BY STEP]
[MISSING: PARALLELIZE AND MAKE IT MORE SIMILAR TO PREVIOUS DATASETS]
8.5 Sanity check for the data
d <- d %>% group_by(agent, strategy) %>% mutate(
nextChoice = lead(choice),
prevWin = lag(win),
prevLose = lag(lose),
cumulativerate = cumsum(choice) / seq_along(choice),
performance = cumsum(feedback) / seq_along(feedback)
) %>% subset(complete.cases(d)) %>% subset(trial > 1)
p1 <- ggplot(d, aes(trial, cumulativerate, group = agent, color = agent)) +
geom_line() +
geom_hline(yintercept = 0.5, linetype = "dashed") + ylim(0,1) + theme_classic() + facet_wrap(.~strategy)
p1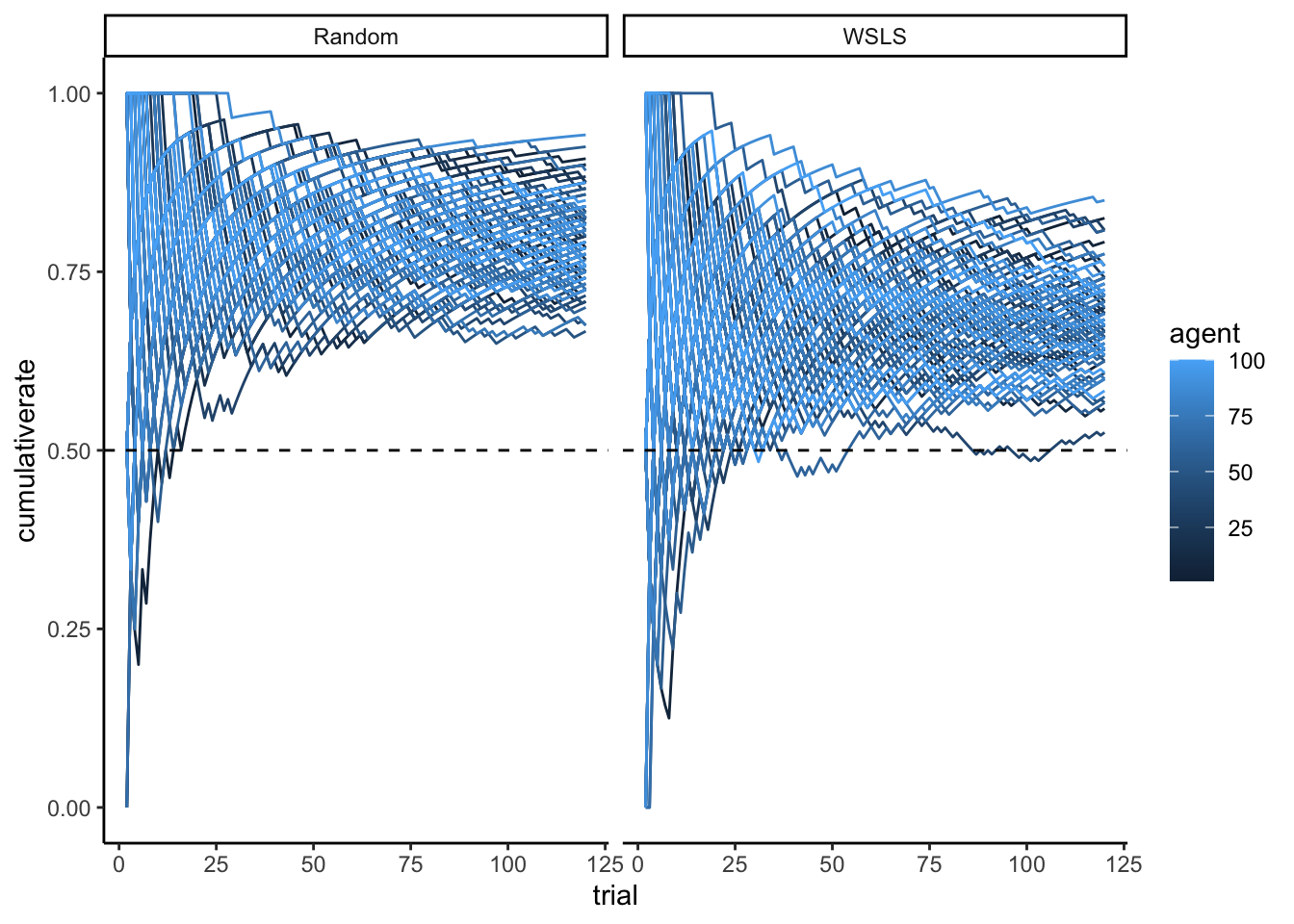
p2a <- ggplot(subset(d, strategy == "Random"), aes(trial, 1 - performance, group = agent, color = agent)) +
geom_line() +
geom_hline(yintercept = 0.5, linetype = "dashed") + ylim(0,1) + theme_classic()
p2b <- ggplot(subset(d, strategy == "WSLS"), aes(trial, performance, group = agent, color = agent)) +
geom_line() +
geom_hline(yintercept = 0.5, linetype = "dashed") + ylim(0,1) + theme_classic()
library(patchwork)
p2a + p2b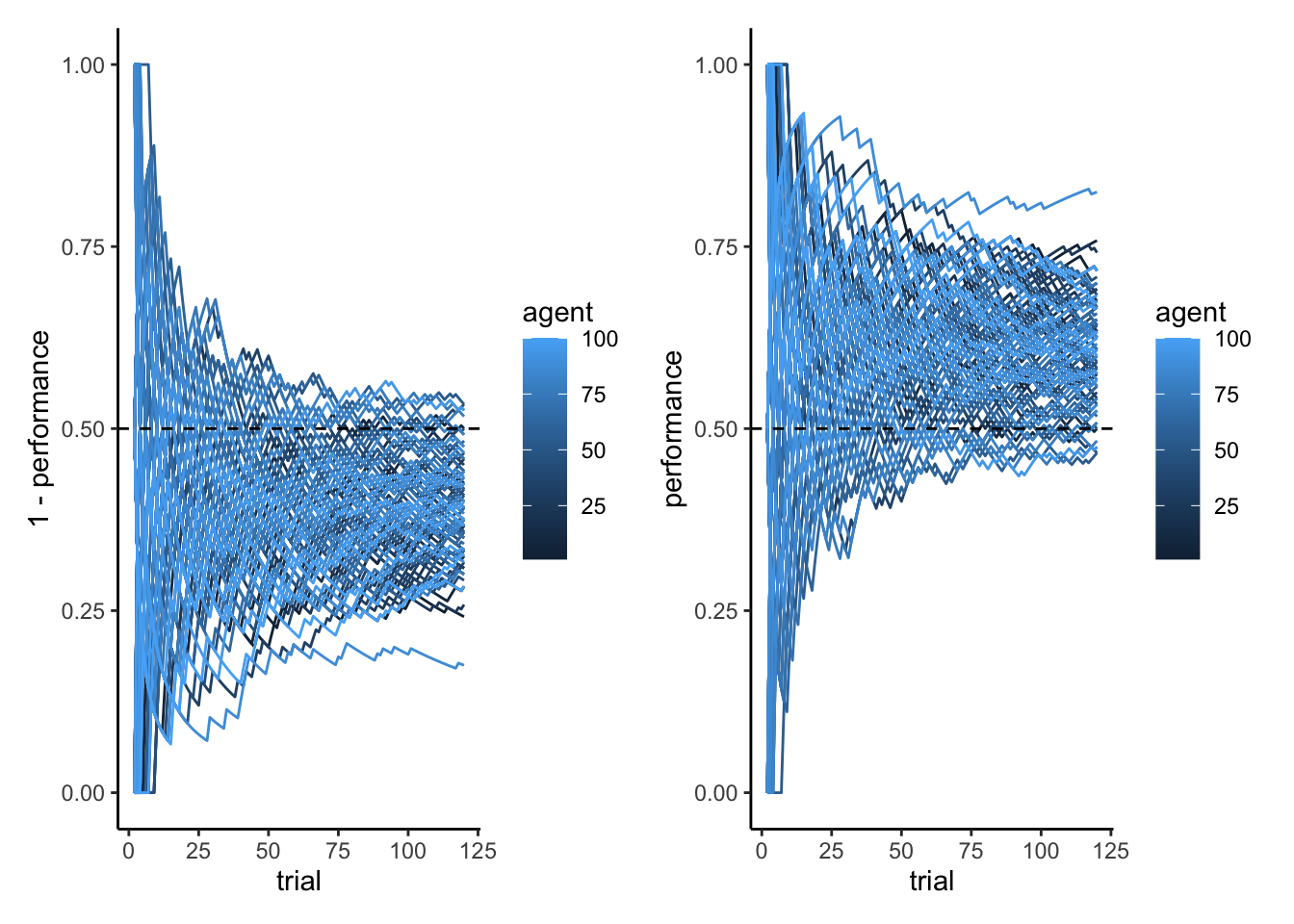
8.6 More sanity check
## Checking lose/win do determine choice
d %>% subset(strategy == "WSLS") %>%
mutate(nextChoice = lead(choice)) %>%
group_by(agent, win, lose) %>%
summarize(heads = mean(nextChoice)) %>%
ggplot(aes(win, heads)) +
geom_point() +
theme_bw() +
facet_wrap(~lose)## `summarise()` has grouped output by 'agent', 'win'. You can override using the
## `.groups` argument.## Warning: Removed 100 rows containing missing values (`geom_point()`).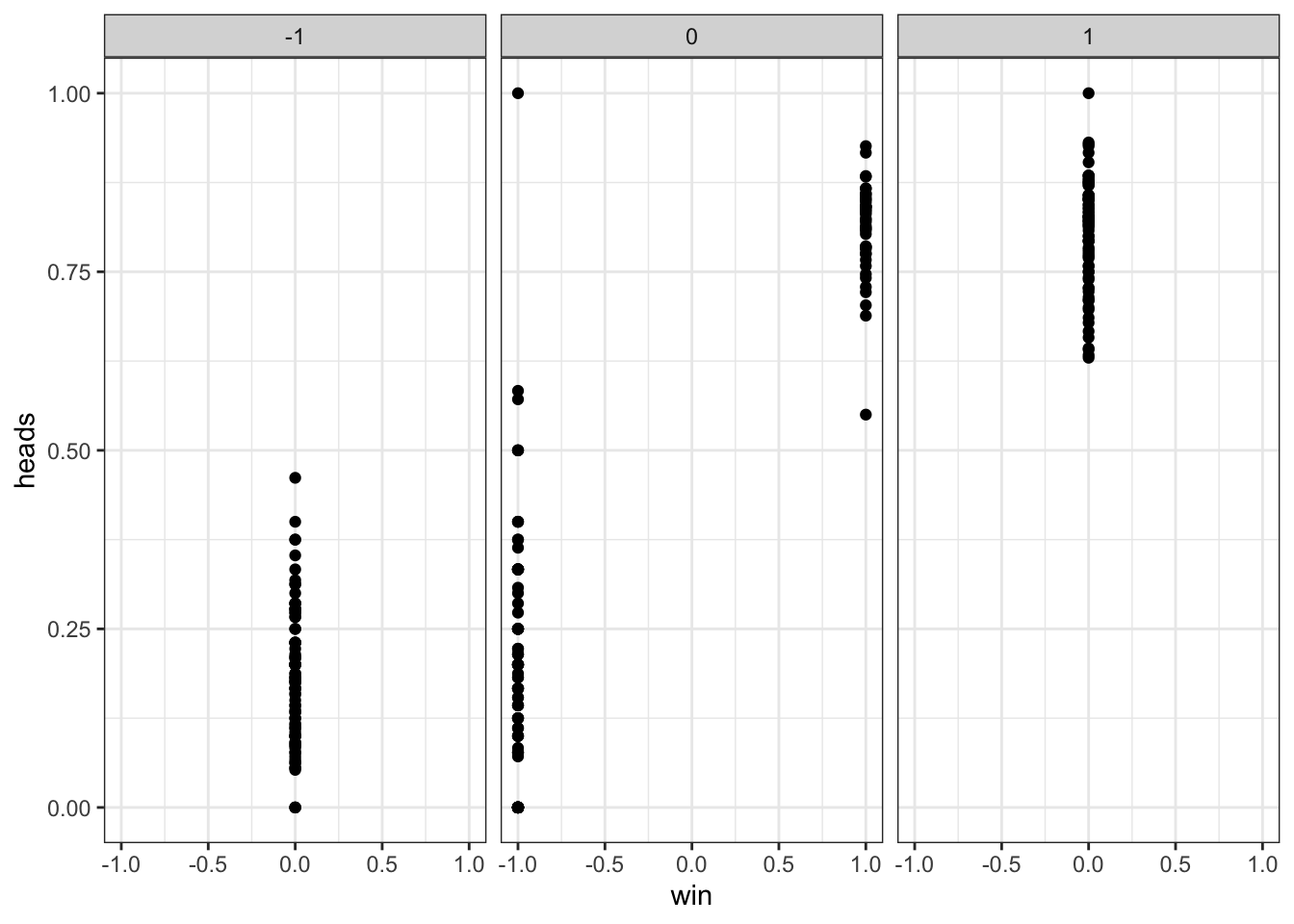
8.8 Create the model
[MISSING: MORE MEANINGFUL PREDICTIONS, BASED ON THE 4 SCENARIOS]
stan_wsls_model <- "
functions{
real normal_lb_rng(real mu, real sigma, real lb) {
real p = normal_cdf(lb | mu, sigma); // cdf for bounds
real u = uniform_rng(p, 1);
return (sigma * inv_Phi(u)) + mu; // inverse cdf for value
}
}
data {
int<lower = 1> trials;
array[trials] int h;
vector[trials] win;
vector[trials] lose;
}
parameters {
real alpha;
real winB;
real loseB;
}
model {
target += normal_lpdf(alpha | 0, .3);
target += normal_lpdf(winB | 1, 1);
target += normal_lpdf(loseB | 1, 1);
target += bernoulli_logit_lpmf(h | alpha + winB * win + loseB * lose);
}
generated quantities{
real alpha_prior;
real winB_prior;
real loseB_prior;
array[trials] int prior_preds;
array[trials] int posterior_preds;
vector[trials] log_lik;
alpha_prior = normal_rng(0, 1);
winB_prior = normal_rng(0, 1);
loseB_prior = normal_rng(0, 1);
prior_preds = bernoulli_rng(inv_logit(winB_prior * win + loseB_prior * lose));
posterior_preds = bernoulli_rng(inv_logit(winB * win + loseB * lose));
for (t in 1:trials){
log_lik[t] = bernoulli_logit_lpmf(h[t] | winB * win + loseB * lose);
}
}
"
write_stan_file(
stan_wsls_model,
dir = "stan/",
basename = "W8_WSLS.stan")## [1] "/Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/stan/W8_WSLS.stan"file <- file.path("stan/W8_WSLS.stan")
mod_wsls_simple <- cmdstan_model(file,
cpp_options = list(stan_threads = TRUE),
stanc_options = list("O1"),
pedantic = TRUE)
samples_wsls_simple <- mod_wsls_simple$sample(
data = data_wsls_simple,
seed = 123,
chains = 2,
parallel_chains = 2,
threads_per_chain = 2,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 1000,
max_treedepth = 20,
adapt_delta = 0.99,
)## Running MCMC with 2 parallel chains, with 2 thread(s) per chain...
##
## Chain 1 Iteration: 1 / 4000 [ 0%] (Warmup)
## Chain 1 Iteration: 1000 / 4000 [ 25%] (Warmup)
## Chain 1 Iteration: 2000 / 4000 [ 50%] (Warmup)
## Chain 1 Iteration: 2001 / 4000 [ 50%] (Sampling)
## Chain 2 Iteration: 1 / 4000 [ 0%] (Warmup)
## Chain 2 Iteration: 1000 / 4000 [ 25%] (Warmup)
## Chain 2 Iteration: 2000 / 4000 [ 50%] (Warmup)
## Chain 2 Iteration: 2001 / 4000 [ 50%] (Sampling)
## Chain 1 Iteration: 3000 / 4000 [ 75%] (Sampling)
## Chain 2 Iteration: 3000 / 4000 [ 75%] (Sampling)
## Chain 1 Iteration: 4000 / 4000 [100%] (Sampling)
## Chain 2 Iteration: 4000 / 4000 [100%] (Sampling)
## Chain 1 finished in 0.6 seconds.
## Chain 2 finished in 0.6 seconds.
##
## Both chains finished successfully.
## Mean chain execution time: 0.6 seconds.
## Total execution time: 0.8 seconds.8.9 Basic assessment
## # A tibble: 364 × 10
## variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 lp__ -7.23e+1 -7.20e+1 1.26 1.04 -74.8 -71.0 1.00 1537. 2227.
## 2 alpha -5.53e-2 -5.34e-2 0.199 0.200 -0.389 0.265 1.00 2359. 2142.
## 3 winB 1.02e+0 1.01e+0 0.297 0.304 0.547 1.52 1.00 2311. 2347.
## 4 loseB 1.10e+0 1.09e+0 0.322 0.311 0.589 1.65 1.00 2208. 2225.
## 5 alpha_prior -1.14e-2 -5.82e-3 0.983 0.959 -1.66 1.57 1.00 4099. 4033.
## 6 winB_prior -1.96e-2 -2.65e-2 0.999 0.996 -1.63 1.67 1.00 4182. 3530.
## 7 loseB_prior 1.86e-4 -5.70e-3 1.01 1.02 -1.65 1.67 1.00 3953. 3659.
## 8 prior_preds[1] 5.05e-1 1 e+0 0.500 0 0 1 1.00 3797. NA
## 9 prior_preds[2] 5.06e-1 1 e+0 0.500 0 0 1 1.00 4120. NA
## 10 prior_preds[3] 5.08e-1 1 e+0 0.500 0 0 1 1.00 3941. NA
## # ℹ 354 more rows# Extract posterior samples and include sampling of the prior:
draws_df <- as_draws_df(samples_wsls_simple$draws())
# Now let's plot the density for theta (prior and posterior)
ggplot(draws_df) +
geom_density(aes(alpha), fill = "blue", alpha = 0.3) +
geom_density(aes(alpha_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = d_a$alpha[1]) +
xlab("Rate") +
ylab("Posterior Density") +
theme_classic()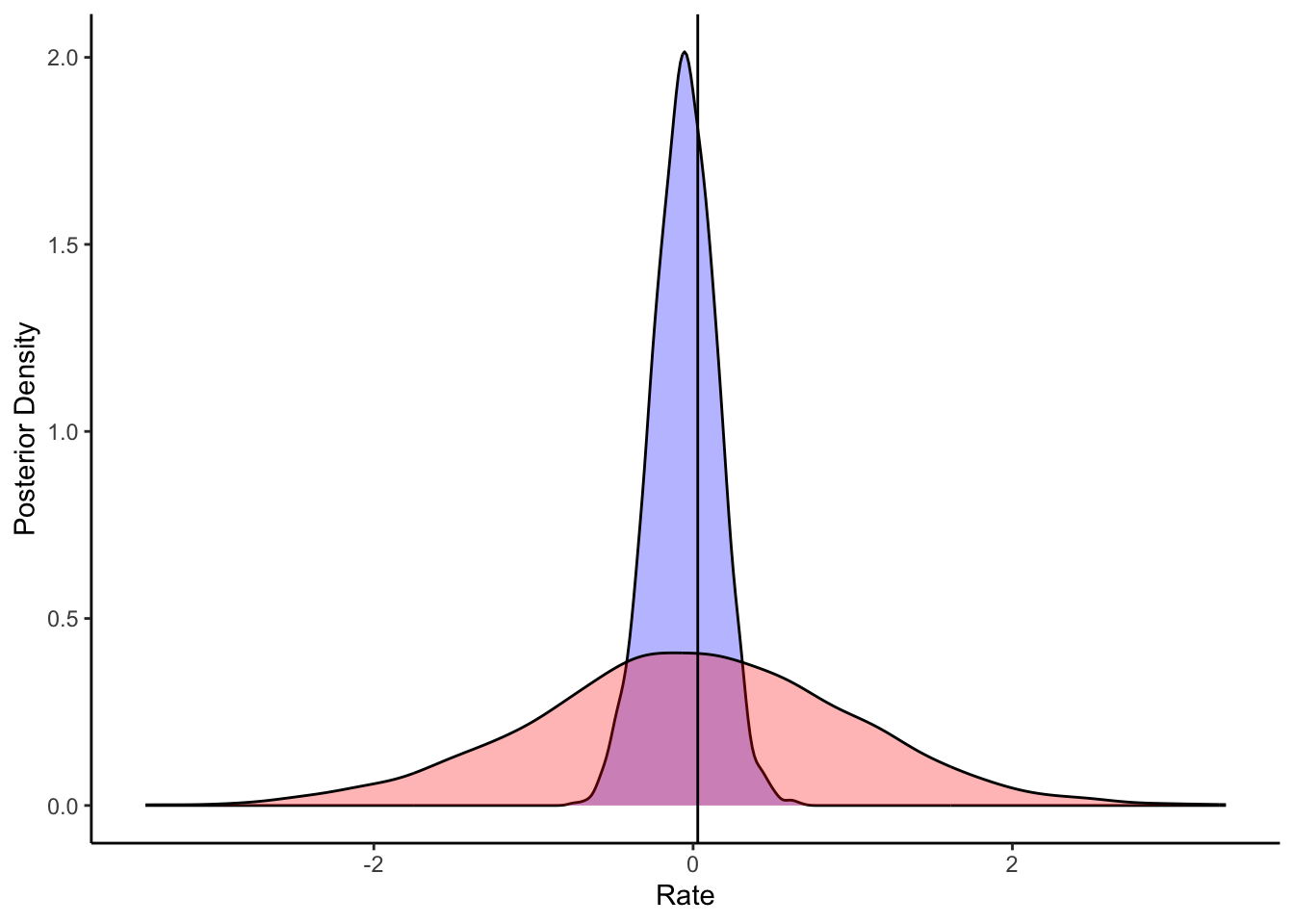
ggplot(draws_df) +
geom_density(aes(winB), fill = "blue", alpha = 0.3) +
geom_density(aes(winB_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = d_a$betaWin[1]) +
xlab("Rate") +
ylab("Posterior Density") +
theme_classic()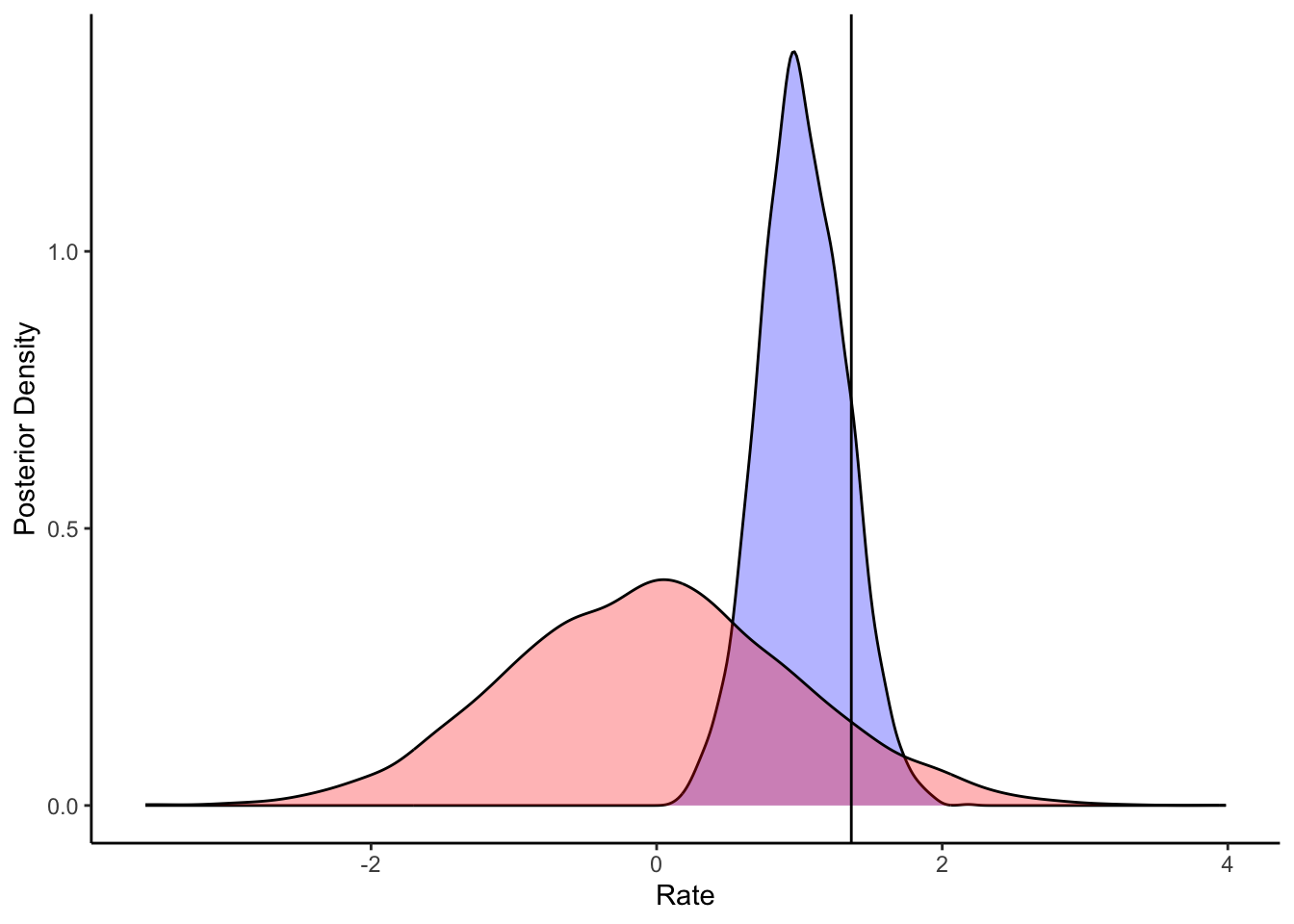
ggplot(draws_df) +
geom_density(aes(loseB), fill = "blue", alpha = 0.3) +
geom_density(aes(loseB_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = d_a$betaLose[1]) +
xlab("Rate") +
ylab("Posterior Density") +
theme_classic()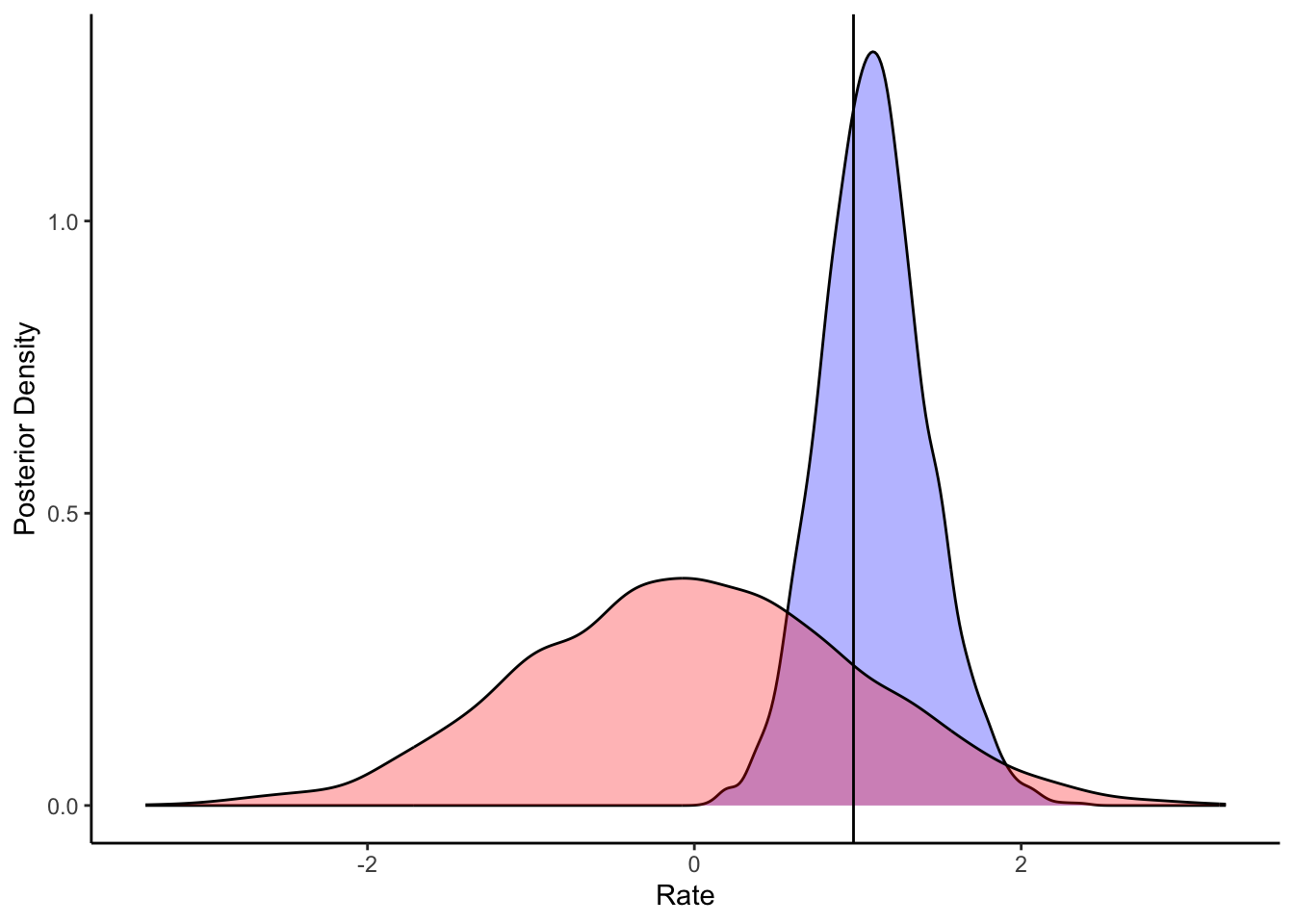
[MISSING: FULL PARAMETER RECOVERY]
8.10 Create multilevel data
## Now multilevel model
d_wsls1 <- d %>% subset(strategy == "WSLS") %>%
subset(select = c(agent, choice)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = choice)
d_wsls2 <- d %>% subset(strategy == "WSLS") %>%
subset(select = c(agent, prevWin)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = prevWin)
d_wsls3 <- d %>% subset(strategy == "WSLS") %>%
subset(select = c(agent, prevLose)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = prevLose)
## Create the data
data_wsls <- list(
trials = trials - 1,
agents = agents,
h = as.matrix(d_wsls1[,2:(agents + 1)]),
win = as.matrix(d_wsls2[,2:(agents + 1)]),
lose = as.matrix(d_wsls3[,2:(agents + 1)])
)8.11 Create the model
[MISSING: ADD BIAS]
[MISSING: BETTER PREDICTIONS BASED ON 4 SCENARIOS]
stan_wsls_ml_model <- "
functions{
real normal_lb_rng(real mu, real sigma, real lb) {
real p = normal_cdf(lb | mu, sigma); // cdf for bounds
real u = uniform_rng(p, 1);
return (sigma * inv_Phi(u)) + mu; // inverse cdf for value
}
}
// The input (data) for the model.
data {
int<lower = 1> trials;
int<lower = 1> agents;
array[trials, agents] int h;
array[trials, agents] real win;
array[trials, agents] real lose;
}
parameters {
real winM;
real loseM;
vector<lower = 0>[2] tau;
matrix[2, agents] z_IDs;
cholesky_factor_corr[2] L_u;
}
transformed parameters {
matrix[agents,2] IDs;
IDs = (diag_pre_multiply(tau, L_u) * z_IDs)';
}
model {
target += normal_lpdf(winM | 0, 1);
target += normal_lpdf(tau[1] | 0, .3) -
normal_lccdf(0 | 0, .3);
target += normal_lpdf(loseM | 0, .3);
target += normal_lpdf(tau[2] | 0, .3) -
normal_lccdf(0 | 0, .3);
target += lkj_corr_cholesky_lpdf(L_u | 2);
target += std_normal_lpdf(to_vector(z_IDs));
for (i in 1:agents)
target += bernoulli_logit_lpmf(h[,i] | to_vector(win[,i]) * (winM + IDs[i,1]) + to_vector(lose[,i]) * (loseM + IDs[i,2]));
}
generated quantities{
real winM_prior;
real<lower=0> winSD_prior;
real loseM_prior;
real<lower=0> loseSD_prior;
real win_prior;
real lose_prior;
array[trials,agents] int<lower=0, upper = trials> prior_preds;
array[trials,agents] int<lower=0, upper = trials> posterior_preds;
array[trials, agents] real log_lik;
winM_prior = normal_rng(0,1);
winSD_prior = normal_lb_rng(0,0.3,0);
loseM_prior = normal_rng(0,1);
loseSD_prior = normal_lb_rng(0,0.3,0);
win_prior = normal_rng(winM_prior, winSD_prior);
lose_prior = normal_rng(loseM_prior, loseSD_prior);
for (i in 1:agents){
prior_preds[,i] = binomial_rng(trials, inv_logit(to_vector(win[,i]) * (win_prior) + to_vector(lose[,i]) * (lose_prior)));
posterior_preds[,i] = binomial_rng(trials, inv_logit(to_vector(win[,i]) * (winM + IDs[i,1]) + to_vector(lose[,i]) * (loseM + IDs[i,2])));
for (t in 1:trials){
log_lik[t,i] = bernoulli_logit_lpmf(h[t,i] | to_vector(win[,i]) * (winM + IDs[i,1]) + to_vector(lose[,i]) * (loseM + IDs[i,2]));
}
}
}
"
write_stan_file(
stan_wsls_ml_model,
dir = "stan/",
basename = "W8_wsls_ml.stan")## [1] "/Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/stan/W8_wsls_ml.stan"file <- file.path("stan/W8_wsls_ml.stan")
mod_wsls <- cmdstan_model(file, cpp_options = list(stan_threads = TRUE),
stanc_options = list("O1"),
pedantic = TRUE)
samples_wsls_ml <- mod_wsls$sample(
data = data_wsls,
seed = 123,
chains = 2,
parallel_chains = 2,
threads_per_chain = 2,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 1000,
max_treedepth = 20,
adapt_delta = 0.99,
)## Running MCMC with 2 parallel chains, with 2 thread(s) per chain...
##
## Chain 1 Iteration: 1 / 4000 [ 0%] (Warmup)
## Chain 2 Iteration: 1 / 4000 [ 0%] (Warmup)
## Chain 2 Iteration: 1000 / 4000 [ 25%] (Warmup)
## Chain 2 Iteration: 2000 / 4000 [ 50%] (Warmup)
## Chain 2 Iteration: 2001 / 4000 [ 50%] (Sampling)
## Chain 1 Iteration: 1000 / 4000 [ 25%] (Warmup)
## Chain 1 Iteration: 2000 / 4000 [ 50%] (Warmup)
## Chain 1 Iteration: 2001 / 4000 [ 50%] (Sampling)
## Chain 2 Iteration: 3000 / 4000 [ 75%] (Sampling)
## Chain 2 Iteration: 4000 / 4000 [100%] (Sampling)
## Chain 2 finished in 15767.0 seconds.
## Chain 1 Iteration: 3000 / 4000 [ 75%] (Sampling)
## Chain 1 Iteration: 4000 / 4000 [100%] (Sampling)
## Chain 1 finished in 24401.6 seconds.
##
## Both chains finished successfully.
## Mean chain execution time: 20084.3 seconds.
## Total execution time: 24401.7 seconds.8.12 Quality checks
## # A tibble: 36,115 × 10
## variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 lp__ -5.94e+3 -5.94e+3 13.4 13.6 -5.97e+3 -5.92e+3 1.00 1010. 1927.
## 2 winM 1.55e+0 1.55e+0 0.0360 0.0352 1.49e+0 1.61e+0 1.00 3142. 2977.
## 3 loseM 1.40e+0 1.40e+0 0.0386 0.0384 1.34e+0 1.47e+0 1.00 4214. 2490.
## 4 tau[1] 2.02e-1 2.04e-1 0.0515 0.0494 1.14e-1 2.84e-1 1.00 1254. 1284.
## 5 tau[2] 1.03e-1 9.99e-2 0.0640 0.0750 9.46e-3 2.11e-1 1.00 830. 1457.
## 6 z_IDs[1,… 9.32e-1 9.29e-1 0.840 0.827 -4.35e-1 2.33e+0 1.00 3706. 2847.
## 7 z_IDs[2,… -2.27e-1 -2.29e-1 1.00 0.993 -1.88e+0 1.46e+0 1.00 4178. 2711.
## 8 z_IDs[1,… -8.61e-1 -8.67e-1 0.824 0.821 -2.22e+0 4.73e-1 1.00 4254. 2943.
## 9 z_IDs[2,… -2.54e-1 -2.54e-1 0.986 0.991 -1.86e+0 1.35e+0 1.00 4290. 2965.
## 10 z_IDs[1,… -9.20e-1 -9.42e-1 0.838 0.819 -2.28e+0 4.67e-1 1.00 4330. 3012.
## # ℹ 36,105 more rows# Extract posterior samples and include sampling of the prior:
draws_df <- as_draws_df(samples_wsls_ml$draws())
# Now let's plot the density for theta (prior and posterior)
ggplot(draws_df) +
geom_density(aes(winM), fill = "blue", alpha = 0.3) +
geom_density(aes(win_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = d$betaWinM[1]) +
xlab("Rate") +
ylab("Posterior Density") +
theme_classic()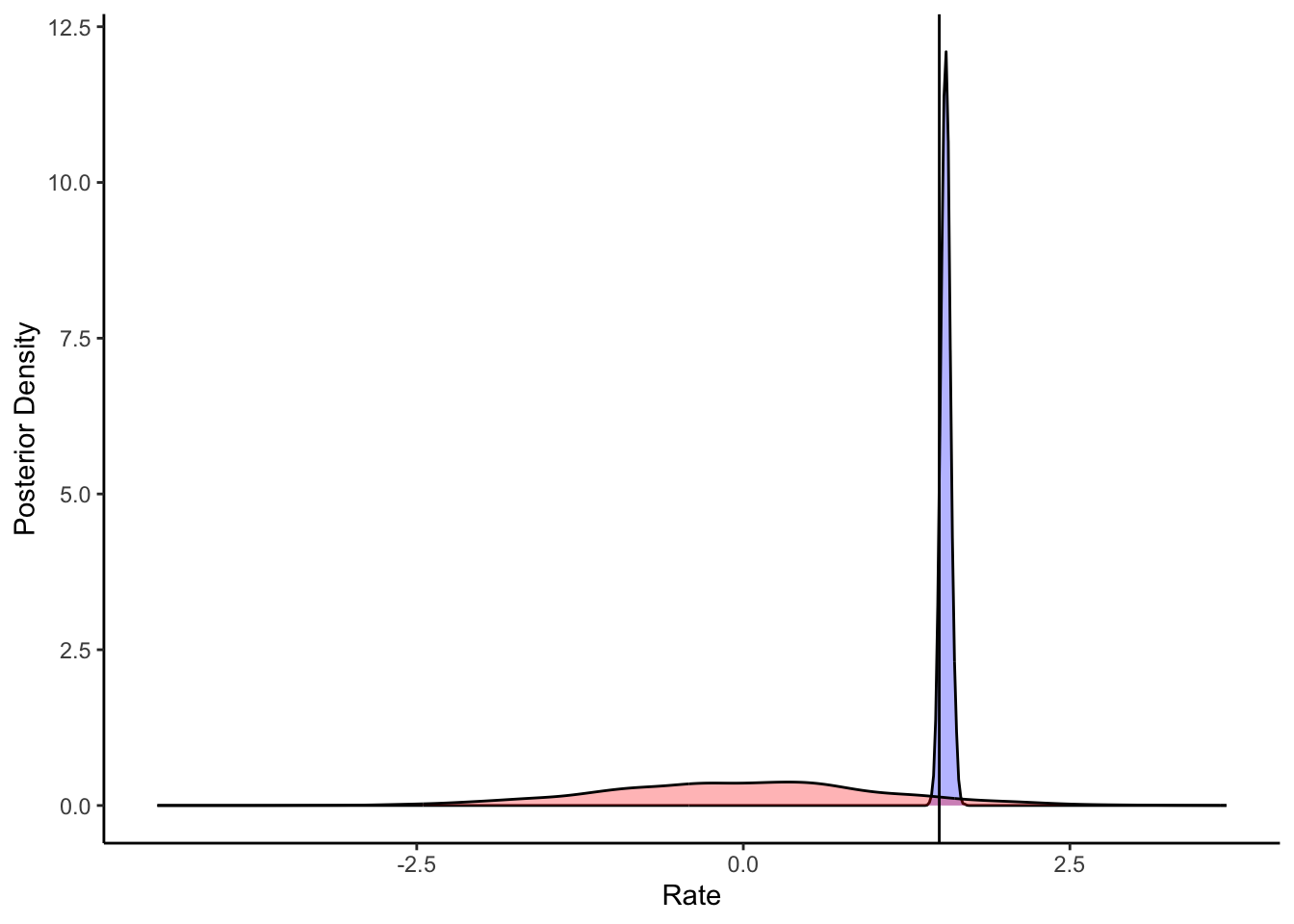
ggplot(draws_df) +
geom_density(aes(`tau[1]`), fill = "blue", alpha = 0.3) +
geom_density(aes(`winSD_prior`), fill = "red", alpha = 0.3) +
geom_vline(xintercept = d$betaWinSD[1]) +
xlab("Rate") +
ylab("Posterior Density") +
theme_classic()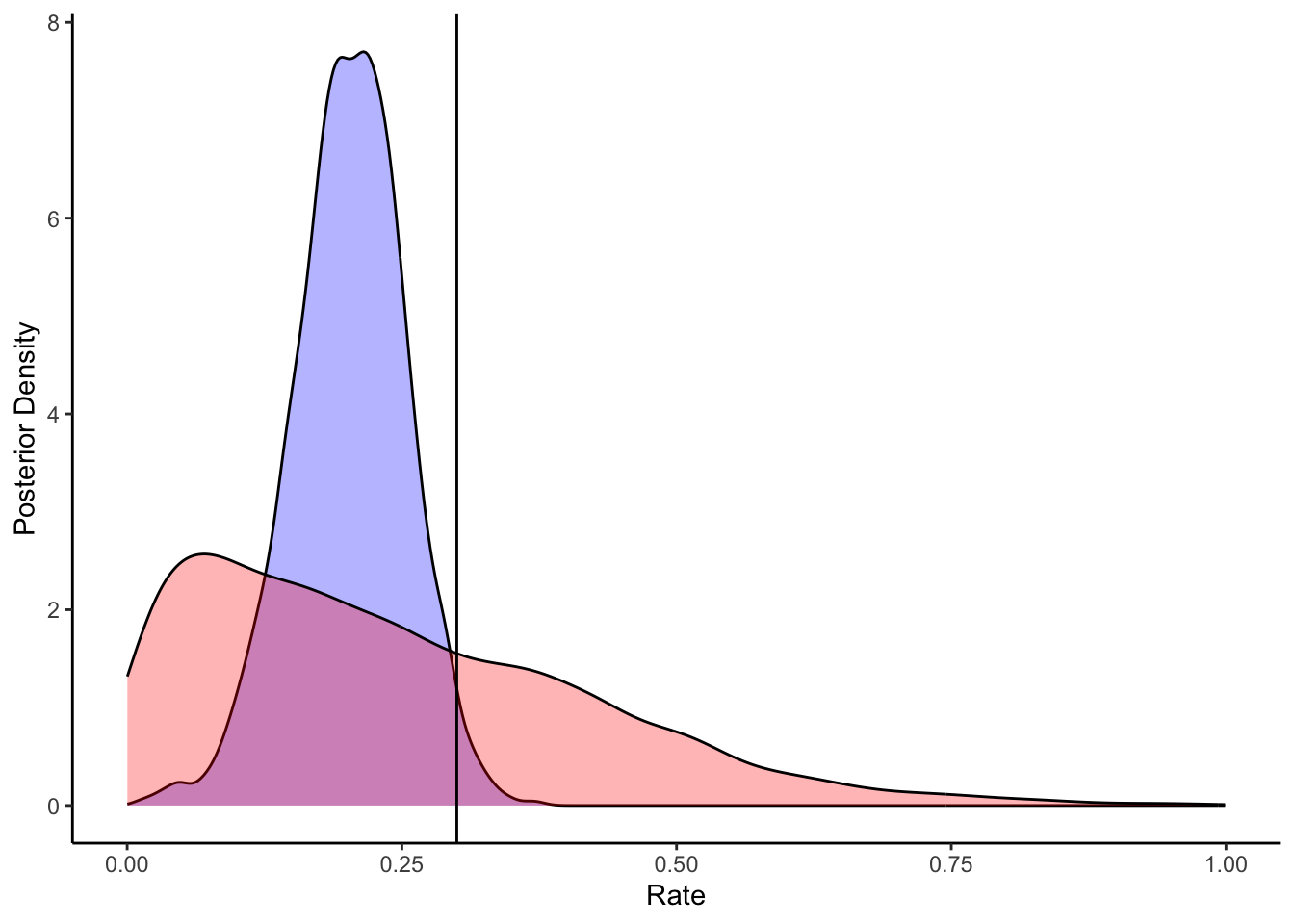
ggplot(draws_df) +
geom_density(aes(loseM), fill = "blue", alpha = 0.3) +
geom_density(aes(loseM_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = d$betaLoseM[1]) +
xlab("Rate") +
ylab("Posterior Density") +
theme_classic()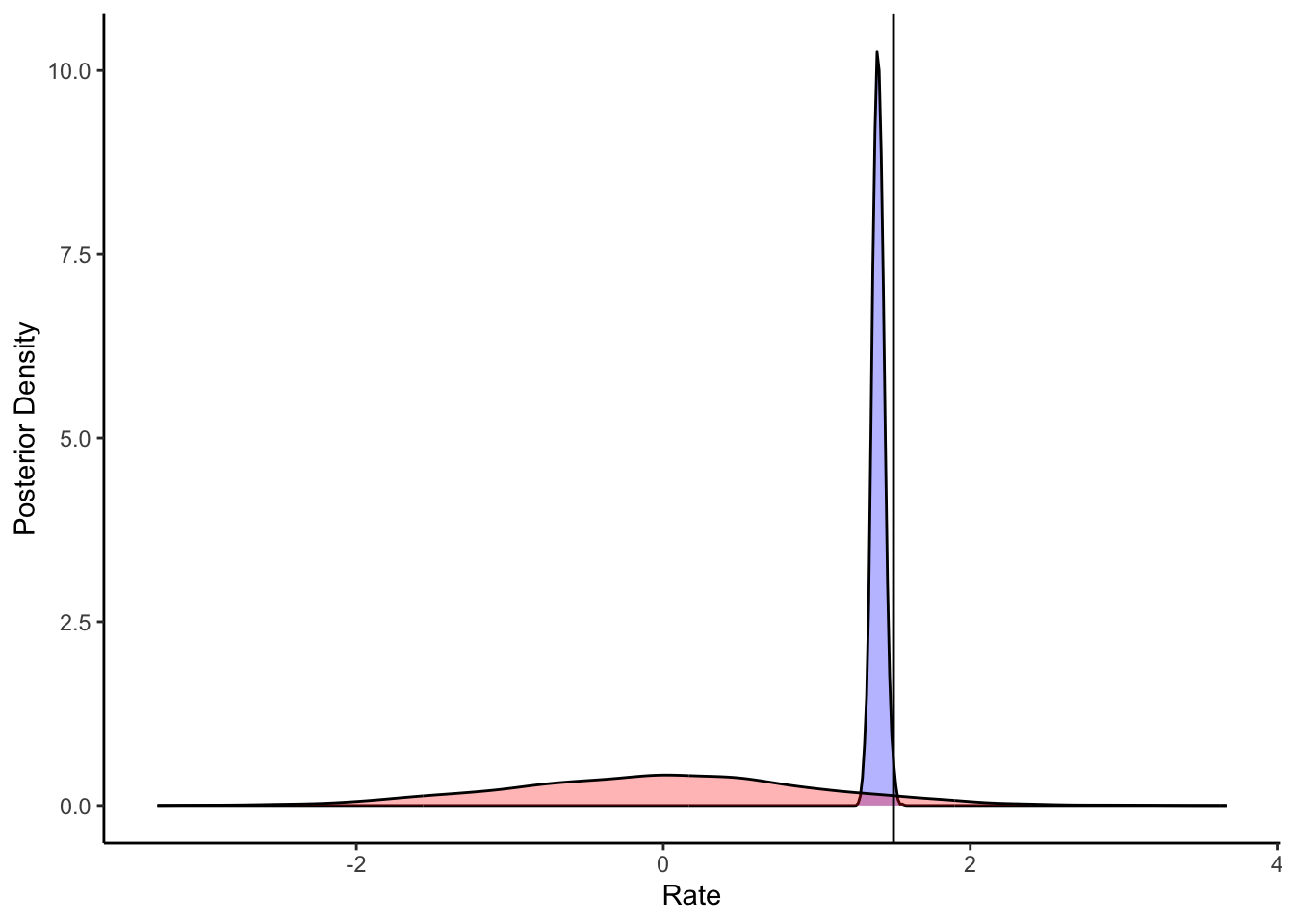
ggplot(draws_df) +
geom_density(aes(`tau[2]`), fill = "blue", alpha = 0.3) +
geom_density(aes(`loseSD_prior`), fill = "red", alpha = 0.3) +
geom_vline(xintercept = d$betaLoseSD[1]) +
xlab("Rate") +
ylab("Posterior Density") +
theme_classic()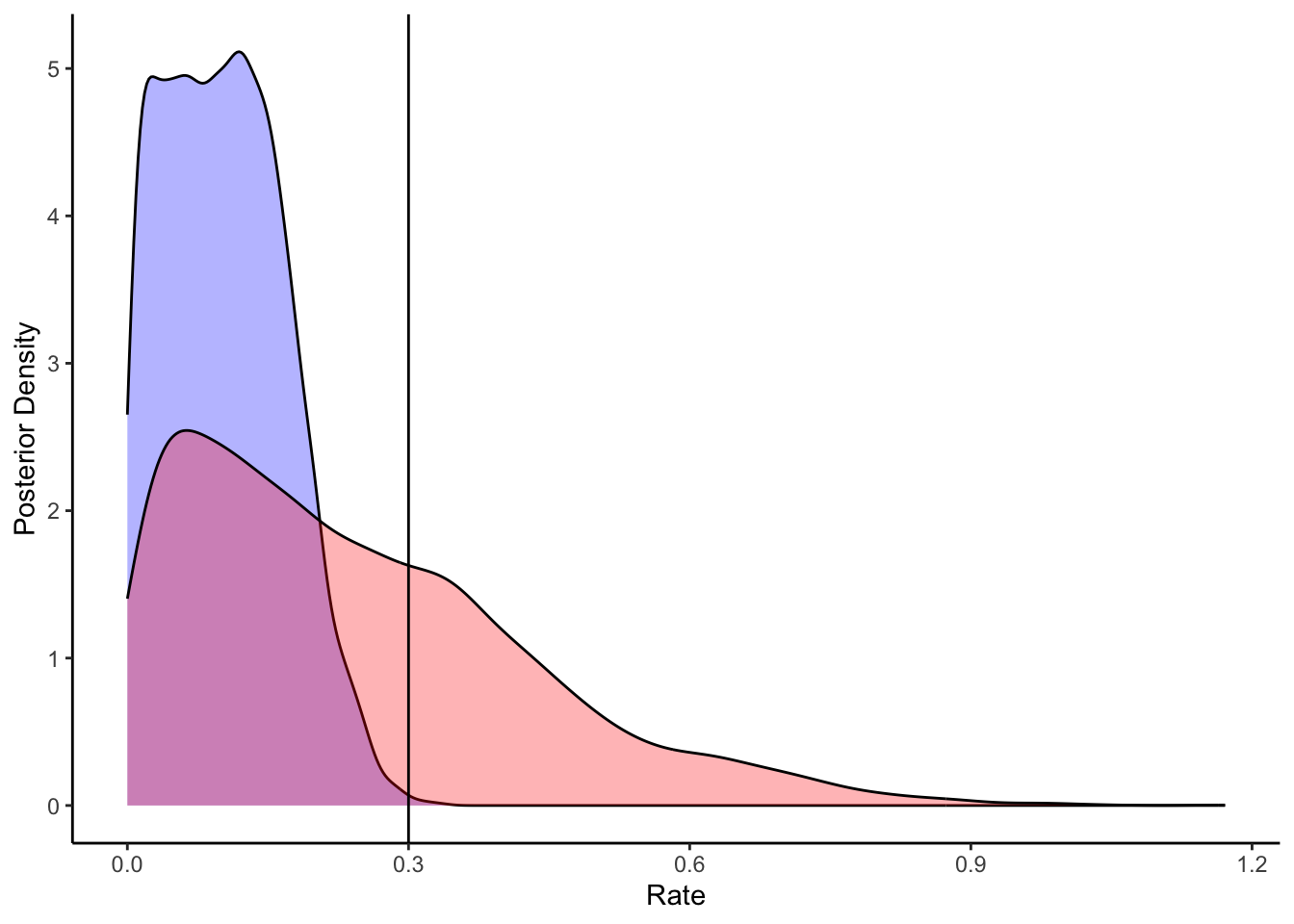
[MISSING: Model comparison with biased] [MISSING: Mixture model with biased]