Chapter 6 Multilevel modeling
6.1 Intro to multilevel modeling
[Explanation on what multilevel modeling is - structure in the data, partial pooling, repeated measures]
6.2 A multilevel version of the biased agent and of the simple memory agent
We are now conceptualizing our agents as being part of (sampled from) a more general population. This general population is characterized by a population level average parameter value (e.g. a general bias of 0.8 as we all like right hands more) and a certain variation in the population (e.g. a standard deviation of 0.1, as we are all a bit different from each other). Each biased agent’s rate is then sampled from that distribution. Same for the memory agents.
[MISSING: DAG PLOTS OF THE TWO SCENARIOS]
Again, it’s practical to work in log odds. Why? Well, it’s not unconceivable that an agent would be 3 sd from the mean. So a biased agent could have a rate of 0.8 + 3 * 0.1, which gives a rate of 1.1. It’s kinda impossible to choose 110% of the time the right hand. We want an easy way to avoid these situations without too carefully tweaking our parameters, or including exception statements (e.g. if rate > 1, then rate = 1). Conversion to log odds is again a wonderful way to work in a boundless space, and in the last step shrinking everything back to 0-1 probability space.
N.B. we model all agents with some added noise as we assume it cannot be eliminated from our studies.
pacman::p_load(tidyverse,
here,
posterior,
cmdstanr,
brms, tidybayes)
# Shared parameters
agents <- 100
trials <- 120
noise <- 0
# Biased agents parameters
rateM <- 1.386 # roughly 0.8 once inv_logit scaled
rateSD <- 0.65 # roughly giving a sd of 0.1 in prob scale
# Memory agents parameters
biasM <- 0
biasSD <- 0.1
betaM <- 1.5
betaSD <- 0.3# Functions of the agents
RandomAgentNoise_f <- function(rate, noise) {
choice <- rbinom(1, 1, inv_logit_scaled(rate))
if (rbinom(1, 1, noise) == 1) {
choice = rbinom(1, 1, 0.5)
}
return(choice)
}
MemoryAgentNoise_f <- function(bias, beta, otherRate, noise) {
rate <- inv_logit_scaled(bias + beta * logit_scaled(otherRate))
choice <- rbinom(1, 1, rate)
if (rbinom(1, 1, noise) == 1) {
choice = rbinom(1, 1, 0.5)
}
return(choice)
}6.3 Generating the agents
[MISSING: PARALLELIZE]
# Looping through all the agents to generate the data.
d <- NULL
for (agent in 1:agents) {
rate <- rnorm(1, rateM, rateSD)
bias <- rnorm(1, biasM, biasSD)
beta <- rnorm(1, betaM, betaSD)
randomChoice <- rep(NA, trials)
memoryChoice <- rep(NA, trials)
memoryRate <- rep(NA, trials)
for (trial in 1:trials) {
randomChoice[trial] <- RandomAgentNoise_f(rate, noise)
if (trial == 1) {
memoryChoice[trial] <- rbinom(1,1,0.5)
} else {
memoryChoice[trial] <- MemoryAgentNoise_f(bias, beta, mean(randomChoice[1:trial], na.rm = T), noise)
}
}
temp <- tibble(agent, trial = seq(trials), randomChoice, randomRate = rate, memoryChoice, memoryRate, noise, rateM, rateSD, bias, beta, biasM, biasSD, betaM, betaSD)
if (agent > 1) {
d <- rbind(d, temp)
} else{
d <- temp
}
}
d <- d %>% group_by(agent) %>% mutate(
randomRate = cumsum(randomChoice) / seq_along(randomChoice),
memoryRate = cumsum(memoryChoice) / seq_along(memoryChoice)
)6.4 Plotting the agents
# A plot of the proportion of right hand choices for the random agents
p1 <- ggplot(d, aes(trial, randomRate, group = agent, color = agent)) +
geom_line(alpha = 0.5) +
geom_hline(yintercept = 0.5, linetype = "dashed") +
ylim(0,1) +
theme_classic()
# A plot of the proportion of right hand choices for the memory agents
p2 <- ggplot(d, aes(trial, memoryRate, group = agent, color = agent)) +
geom_line(alpha = 0.5) +
geom_hline(yintercept = 0.5, linetype = "dashed") +
ylim(0,1) +
theme_classic()
p1 + p2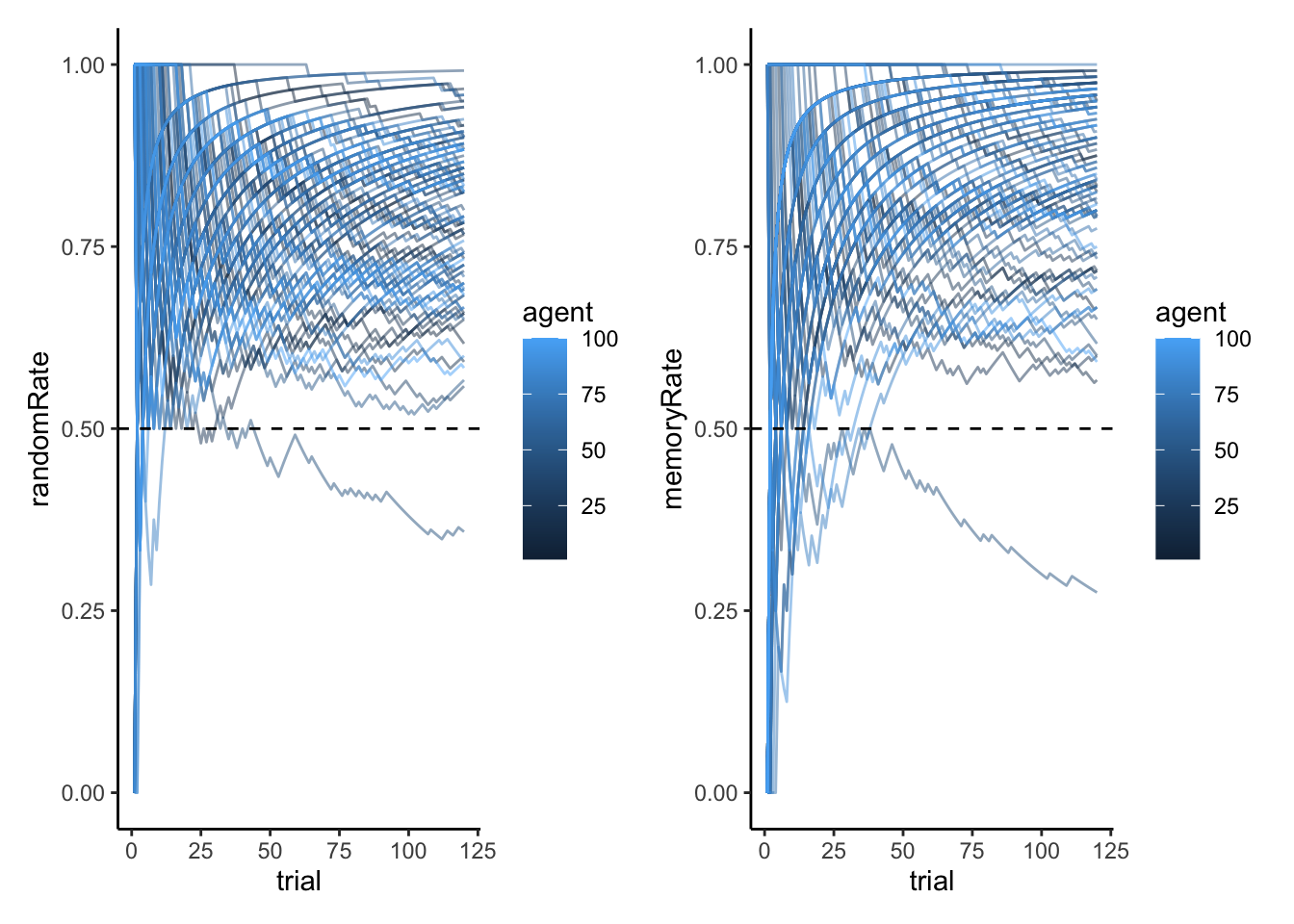
# A plot of whether memory and random agents are matched in proportion at different stages
p3 <- d %>% subset(trial == 10) %>% ggplot(aes(randomRate, memoryRate)) +
geom_point() +
geom_smooth(method = lm) +
geom_abline(intercept = 0, slope = 1, color = "red") +
xlim(0.25, 1) +
ylim(0.25, 1) +
xlab("correlation at 10 trials") +
theme_bw()
p4 <- d %>% subset(trial == 60) %>% ggplot(aes(randomRate, memoryRate)) +
geom_point() +
geom_smooth(method = lm) +
geom_abline(intercept = 0, slope = 1, color = "red") +
xlim(0.25, 1) +
ylim(0.25, 1) +
xlab("correlation at 60 trials") +
theme_bw()
p5 <- d %>% subset(trial == 120) %>% ggplot(aes(randomRate, memoryRate)) +
geom_point() +
geom_smooth(method = lm) +
geom_abline(intercept = 0, slope = 1, color = "red") +
xlim(0.25, 1) +
ylim(0.25, 1) +
xlab("correlation at 120 trials") +
theme_bw()
p3 + p4 + p5## `geom_smooth()` using formula = 'y ~ x'
## `geom_smooth()` using formula = 'y ~ x'## Warning: Removed 7 rows containing missing values (`geom_smooth()`).## `geom_smooth()` using formula = 'y ~ x'## Warning: Removed 6 rows containing missing values (`geom_smooth()`).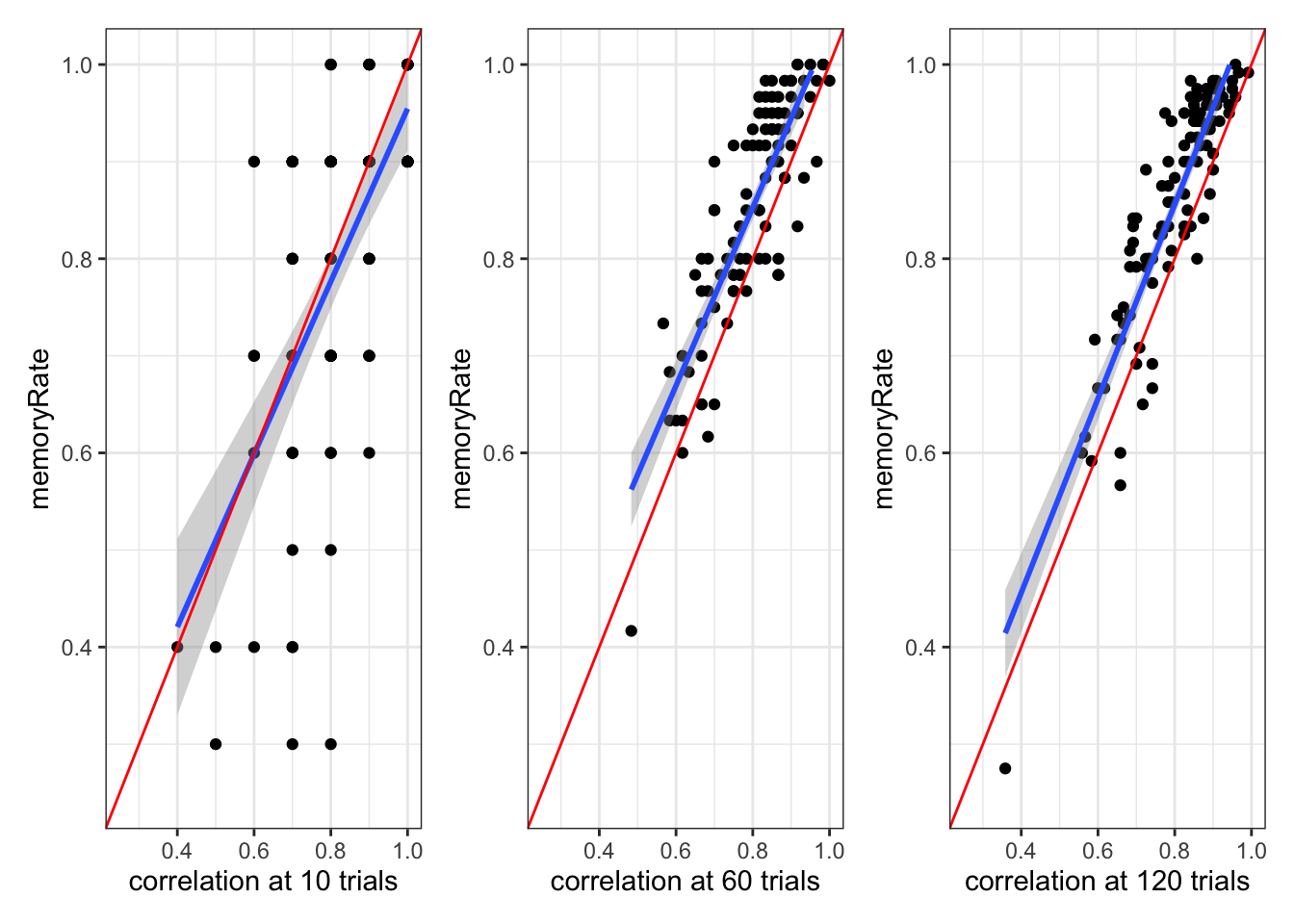
Note that as the n of trials increases, the memory model matches the random model better and better
6.5 Coding the multilevel agents
6.5.1 Multilevel random
Remember that the simulated parameters are: * biasM <- 0 * biasSD <- 0.1 * betaM <- 1.5 * betaSD <- 0.3
Prep the data
d1 <- d %>%
subset(select = c(agent, randomChoice)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = randomChoice)
## Create the data
data <- list(
trials = trials,
agents = agents,
h = as.matrix(d1[,2:101])
)stan_model <- "
//
// This STAN model infers a random bias from a sequences of 1s and 0s (right and left). Now multilevel
//
functions{
real normal_lb_rng(real mu, real sigma, real lb) { // normal distribution with a lower bound
real p = normal_cdf(lb | mu, sigma); // cdf for bounds
real u = uniform_rng(p, 1);
return (sigma * inv_Phi(u)) + mu; // inverse cdf for value
}
}
// The input (data) for the model. n of trials and h of hands
data {
int<lower = 1> trials;
int<lower = 1> agents;
array[trials, agents] int h;
}
// The parameters accepted by the model.
parameters {
real thetaM;
real<lower = 0> thetaSD;
array[agents] real theta;
}
// The model to be estimated.
model {
target += normal_lpdf(thetaM | 0, 1);
target += normal_lpdf(thetaSD | 0, .3) -
normal_lccdf(0 | 0, .3);
// The prior for theta is a uniform distribution between 0 and 1
target += normal_lpdf(theta | thetaM, thetaSD);
for (i in 1:agents)
target += bernoulli_logit_lpmf(h[,i] | theta[i]);
}
generated quantities{
real thetaM_prior;
real<lower=0> thetaSD_prior;
real<lower=0, upper=1> theta_prior;
real<lower=0, upper=1> theta_posterior;
int<lower=0, upper = trials> prior_preds;
int<lower=0, upper = trials> posterior_preds;
thetaM_prior = normal_rng(0,1);
thetaSD_prior = normal_lb_rng(0,0.3,0);
theta_prior = inv_logit(normal_rng(thetaM_prior, thetaSD_prior));
theta_posterior = inv_logit(normal_rng(thetaM, thetaSD));
prior_preds = binomial_rng(trials, inv_logit(thetaM_prior));
posterior_preds = binomial_rng(trials, inv_logit(thetaM));
}
"
write_stan_file(
stan_model,
dir = "stan/",
basename = "W5_MultilevelBias.stan")
file <- file.path("stan/W5_MultilevelBias.stan")
mod <- cmdstan_model(file,
cpp_options = list(stan_threads = TRUE),
stanc_options = list("O1"))
# The following command calls Stan with specific options.
samples <- mod$sample(
data = data,
seed = 123,
chains = 2,
parallel_chains = 2,
threads_per_chain = 2,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 500,
max_treedepth = 20,
adapt_delta = 0.99,
)
samples$save_object(file = "simmodels/W5_MultilevelBias.RDS")6.5.2 Assessing multilevel random agents
Besides the usual prior predictive checks, prior posterior update checks, posterior predictive checks, based on the population level estimates; we also want to plot at least a few of the single agents to assess how well the model is doing for them.
[MISSING: PLOT MODEL ESTIMATES AGAINST N OF HEADS BY PARTICIPANT]
## File /var/folders/lt/zspkqnxd5yg92kybm5f433_cfjr0d6/T/RtmpTP5vj3/W5_MultilevelBias-202303101235-1-84831d.csv not found
## File /var/folders/lt/zspkqnxd5yg92kybm5f433_cfjr0d6/T/RtmpTP5vj3/W5_MultilevelBias-202303101235-2-84831d.csv not found
## No valid input files, exiting.## # A tibble: 109 × 10
## variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 lp__ -5780. -5780. 7.26 7.35 -5792. -5.77e+3 1.00 1370. 2125.
## 2 thetaM 1.49 1.49 0.0664 0.0678 1.38 1.60e+0 1.00 7644. 3557.
## 3 thetaSD 0.637 0.634 0.0523 0.0526 0.557 7.27e-1 1.00 5220. 3381.
## 4 theta[1] 0.663 0.661 0.184 0.188 0.366 9.68e-1 1.00 8209. 2723.
## 5 theta[2] 0.909 0.909 0.190 0.195 0.604 1.22e+0 1.00 10277. 2844.
## 6 theta[3] 1.28 1.27 0.216 0.213 0.932 1.64e+0 1.00 9117. 2544.
## 7 theta[4] 2.16 2.15 0.274 0.279 1.73 2.62e+0 1.00 8381. 2508.
## 8 theta[5] 1.51 1.50 0.217 0.214 1.16 1.86e+0 1.00 8492. 2303.
## 9 theta[6] 2.32 2.31 0.281 0.273 1.88 2.80e+0 1.00 9372. 2814.
## 10 theta[7] 2.10 2.09 0.275 0.267 1.66 2.57e+0 1.00 9292. 2740.
## # ℹ 99 more rowsdraws_df <- as_draws_df(samples$draws())
ggplot(draws_df, aes(.iteration, thetaM, group = .chain, color = .chain)) +
geom_line(alpha = 0.5) +
theme_classic()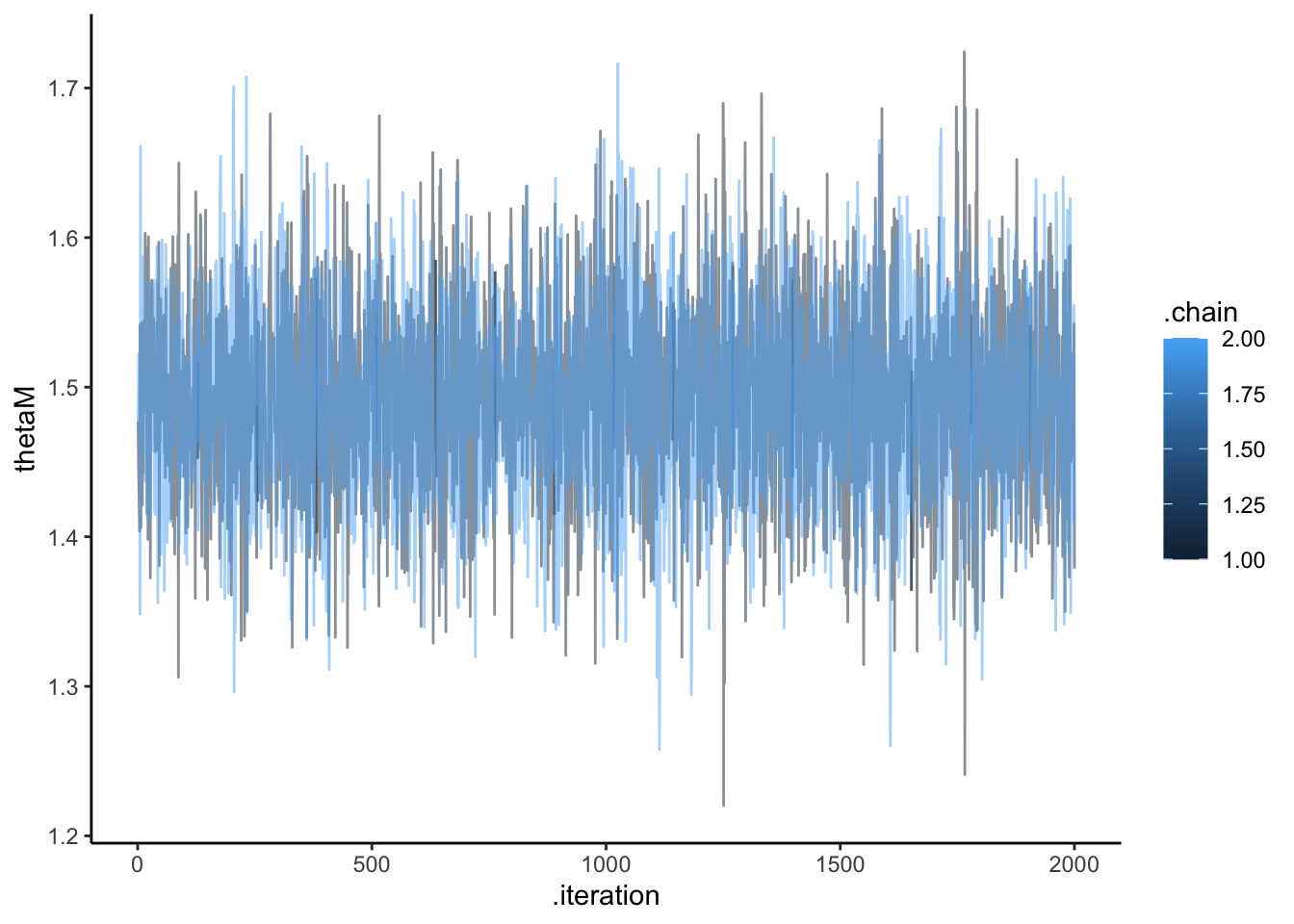
ggplot(draws_df, aes(.iteration, thetaSD, group = .chain, color = .chain)) +
geom_line(alpha = 0.5) +
theme_classic()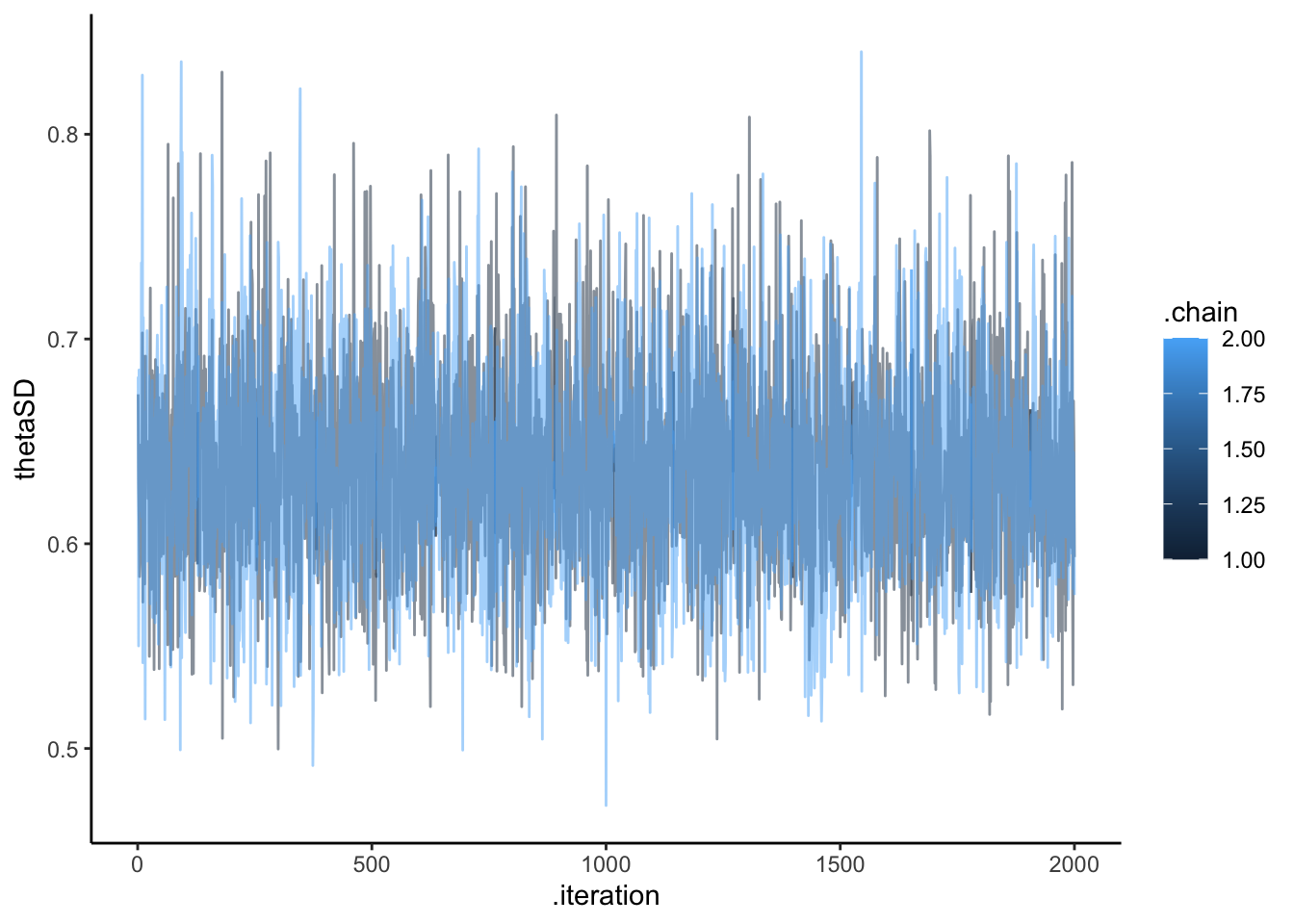
ggplot(draws_df) +
geom_histogram(aes(prior_preds), color = "darkblue", fill = "blue", alpha = 0.3) +
xlab("Predicted right hands out of 120 trials") +
ylab("Prior Density") +
theme_classic()## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.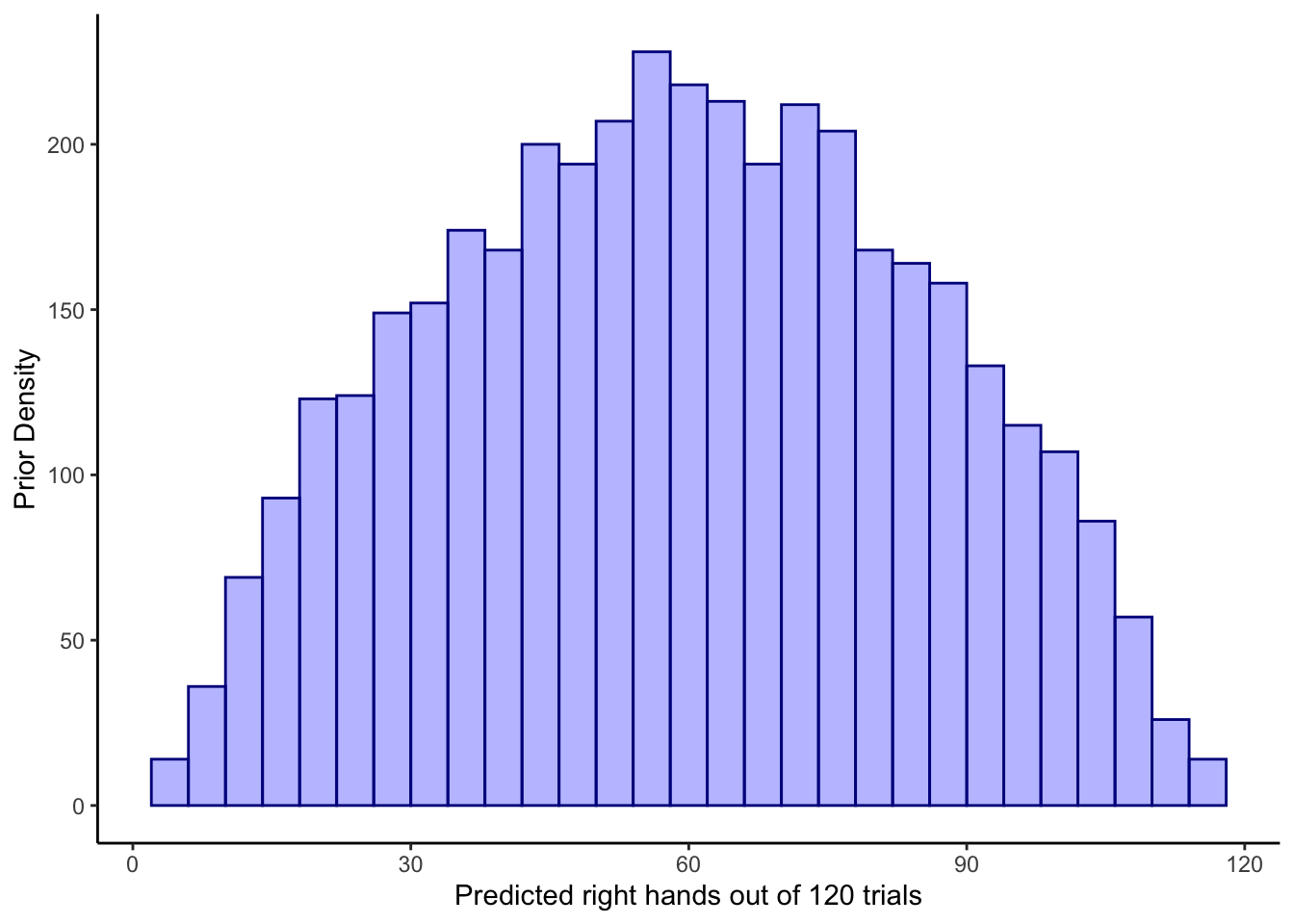
ggplot(draws_df) +
geom_density(aes(thetaM), fill = "blue", alpha = 0.3) +
geom_density(aes(thetaM_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = 1.386) +
xlab("Mean Rate") +
ylab("Posterior Density") +
theme_classic()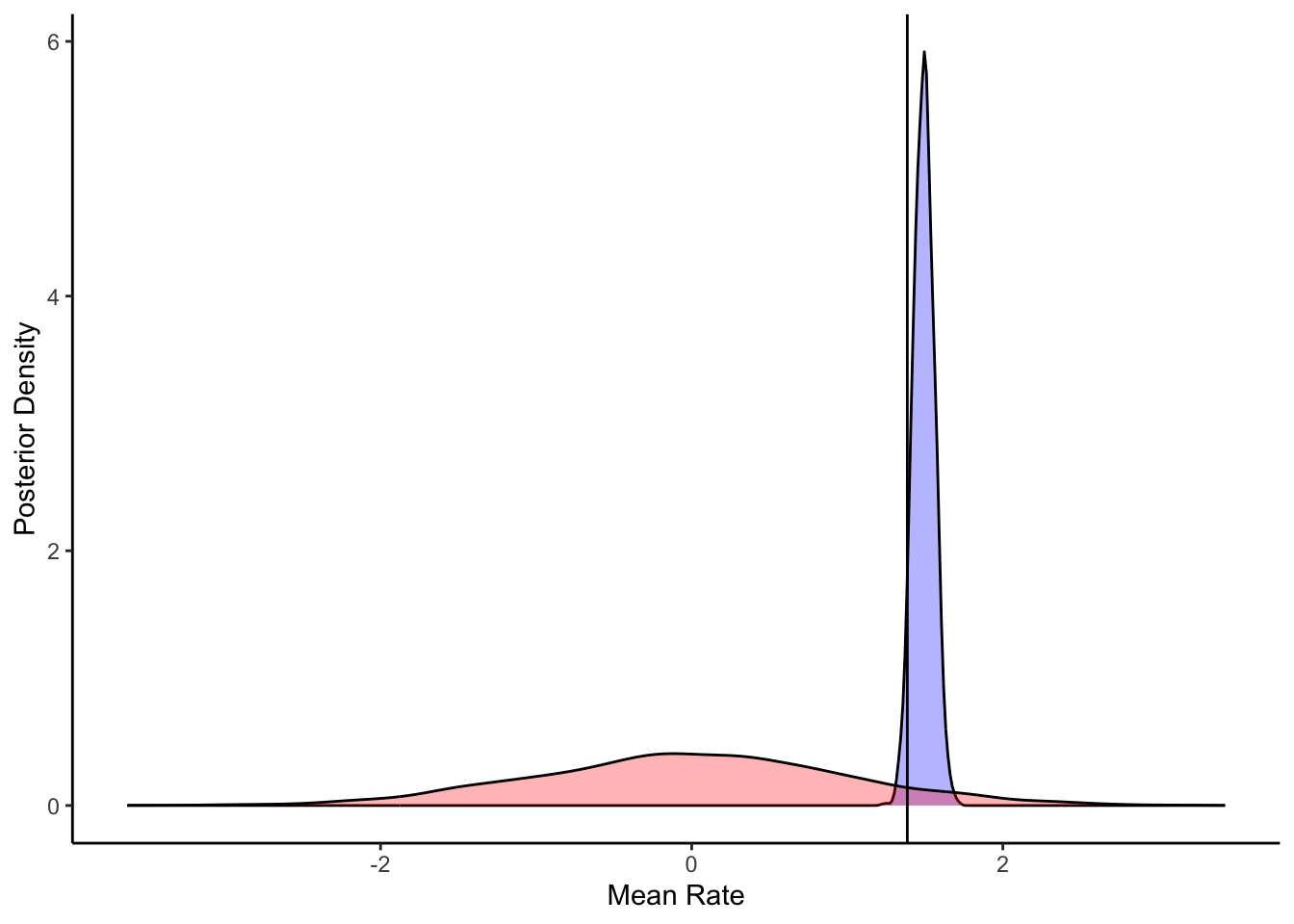
ggplot(draws_df) +
geom_density(aes(thetaSD), fill = "blue", alpha = 0.3) +
geom_density(aes(thetaSD_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = 0.65) +
xlab("Variance of Rate") +
ylab("Posterior Density") +
theme_classic()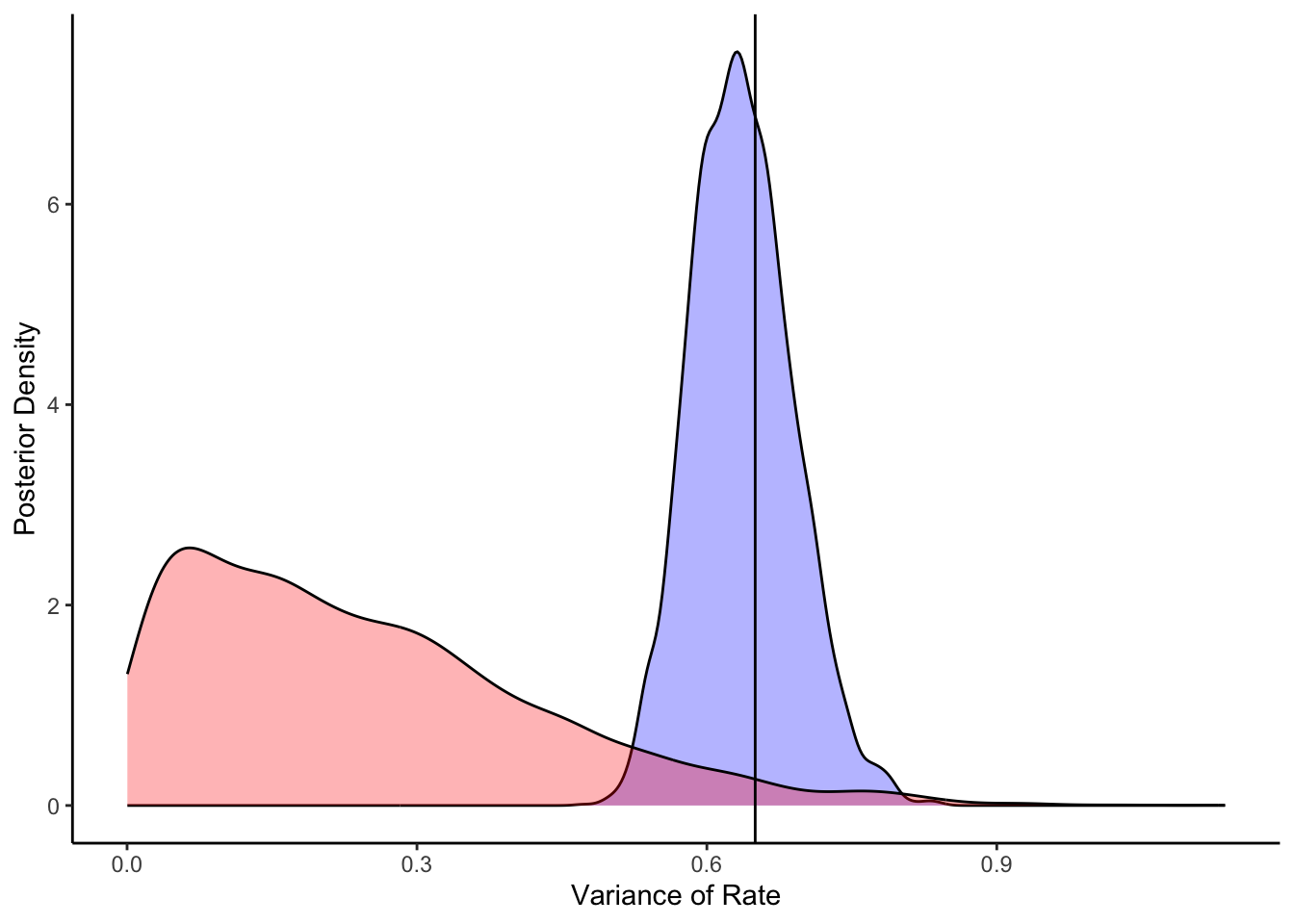
ggplot(draws_df) +
geom_density(aes(theta_posterior), fill = "blue", alpha = 0.3) +
geom_density(aes(theta_prior), fill = "red", alpha = 0.3) +
xlab("Overall Rate") +
ylab("Posterior Density") +
theme_classic()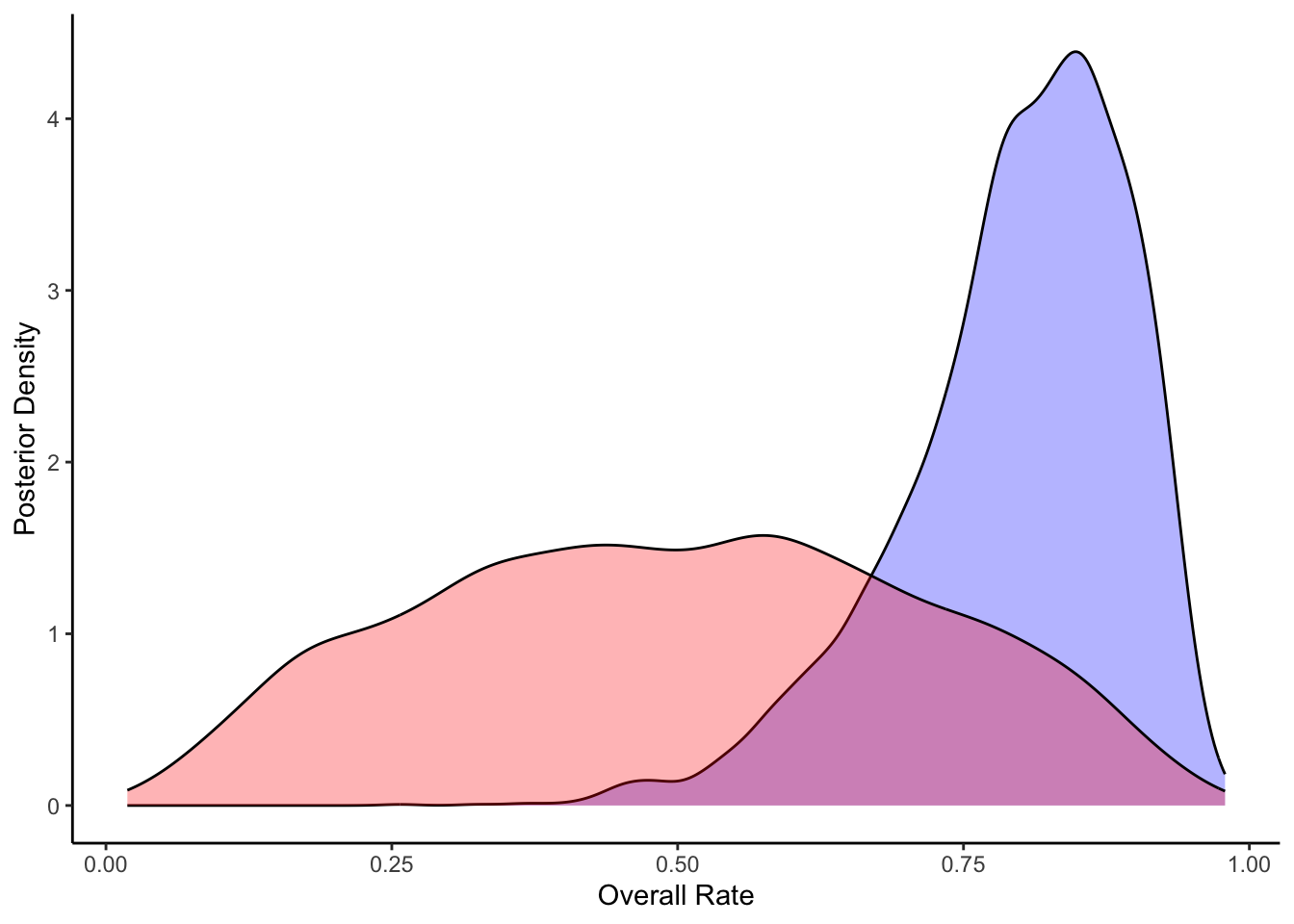
ggplot(draws_df) +
geom_histogram(aes(prior_preds), color = "darkblue", fill = "lightblue", alpha = 0.3) +
geom_histogram(aes(posterior_preds), color = "darkblue", fill = "blue", alpha = 0.3) +
xlab("Predicted right hands out of 120 trials") +
ylab("Predictive Density") +
theme_classic()## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.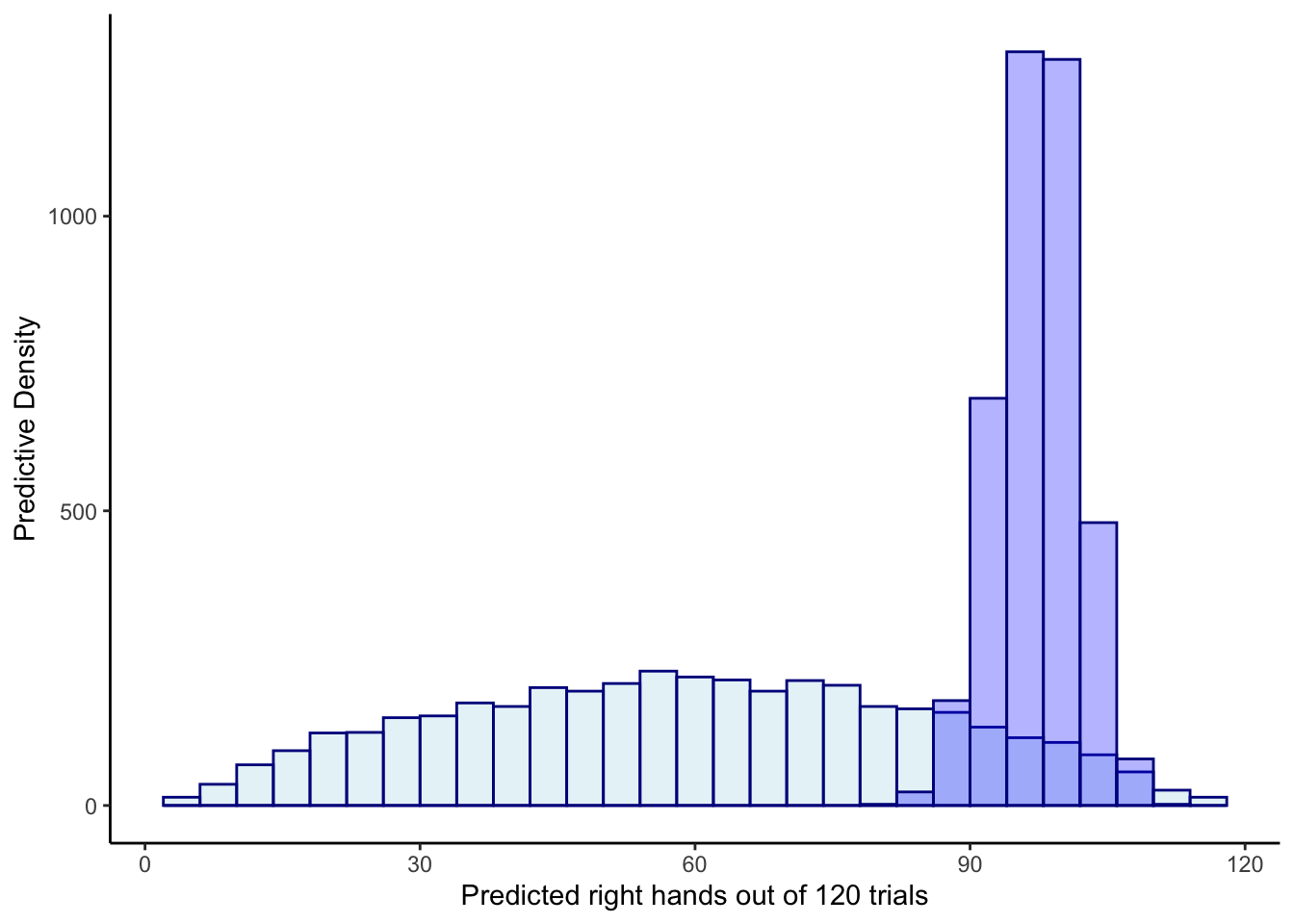
ggplot(draws_df) +
geom_density(aes(inv_logit_scaled(`theta[1]`)), fill = "blue", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`theta[15]`)), fill = "green", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`theta[21]`)), fill = "lightblue", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`theta[31]`)), fill = "darkblue", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`theta[41]`)), fill = "yellow", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`theta[51]`)), fill = "darkgreen", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`theta[61]`)), fill = "lightgreen", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(thetaM_prior)), fill = "pink", alpha = 0.3) +
geom_density(aes(theta_prior), fill = "purple", alpha = 0.3) +
xlab("Mean Rate") +
ylab("Posterior Density") +
theme_classic()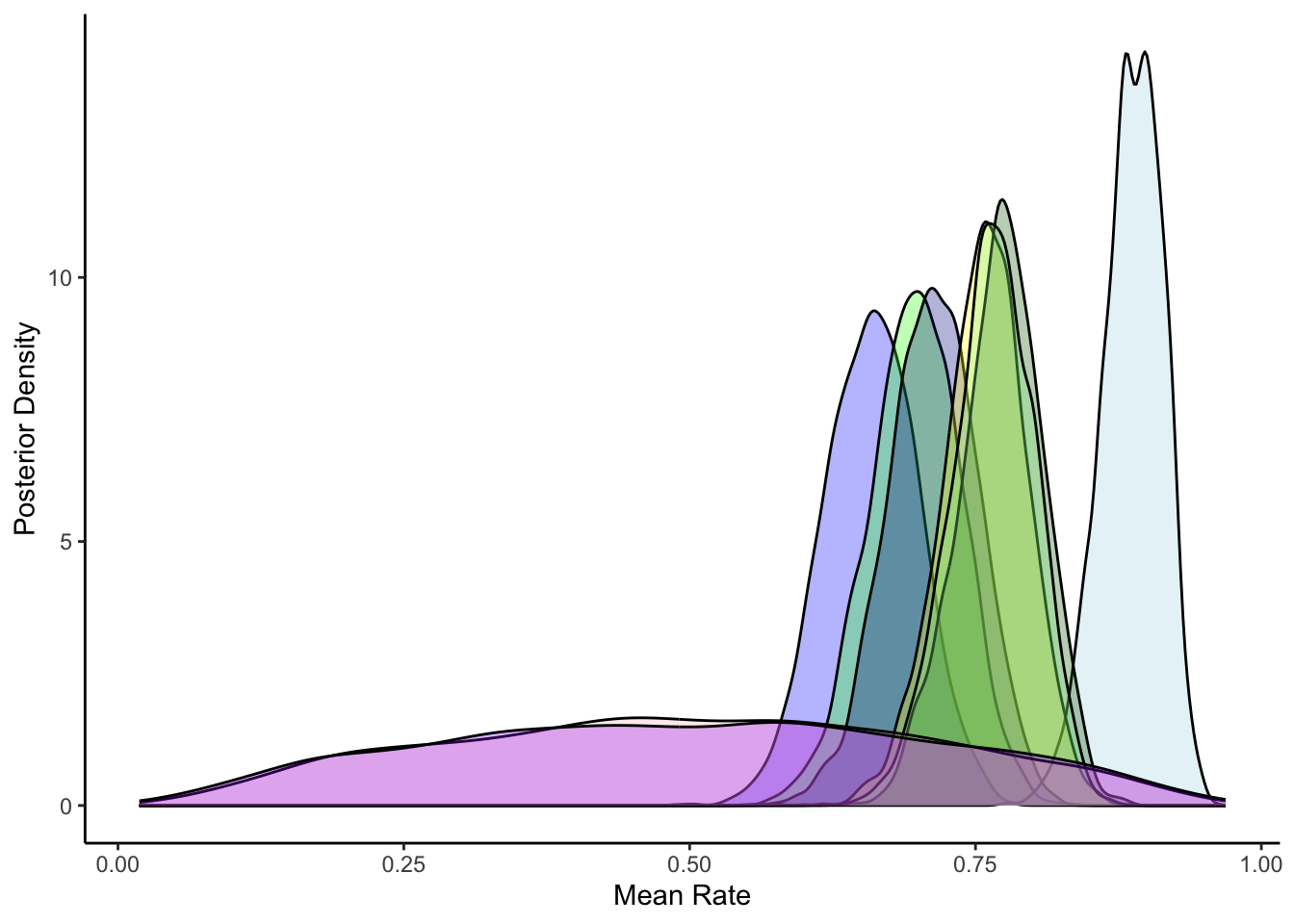
draws_df <- draws_df %>% mutate(
preds1 = rbinom(4000,120, inv_logit_scaled(`theta[1]`)),
preds11 = rbinom(4000,120, inv_logit_scaled(`theta[11]`)),
preds21 = rbinom(4000,120, inv_logit_scaled(`theta[21]`)),
preds31 = rbinom(4000,120, inv_logit_scaled(`theta[31]`)),
preds41 = rbinom(4000,120, inv_logit_scaled(`theta[41]`)),
preds51 = rbinom(4000,120, inv_logit_scaled(`theta[51]`)),
preds61 = rbinom(4000,120, inv_logit_scaled(`theta[61]`)),
preds71 = rbinom(4000,120, inv_logit_scaled(`theta[71]`)),
preds81 = rbinom(4000,120, inv_logit_scaled(`theta[81]`)),
preds91 = rbinom(4000,120, inv_logit_scaled(`theta[91]`)),
)
d2 <- d %>% group_by(agent) %>% dplyr::summarise(right = sum(randomChoice))
ggplot(draws_df) +
geom_density(aes(posterior_preds), color = "skyblue1", alpha = 0.3) +
geom_density(data = d2, aes(right), color = "darkblue",alpha = 0.8) +
xlab("Predicted right hands out of 120 trials") +
ylab("Posterior Density") +
theme_classic()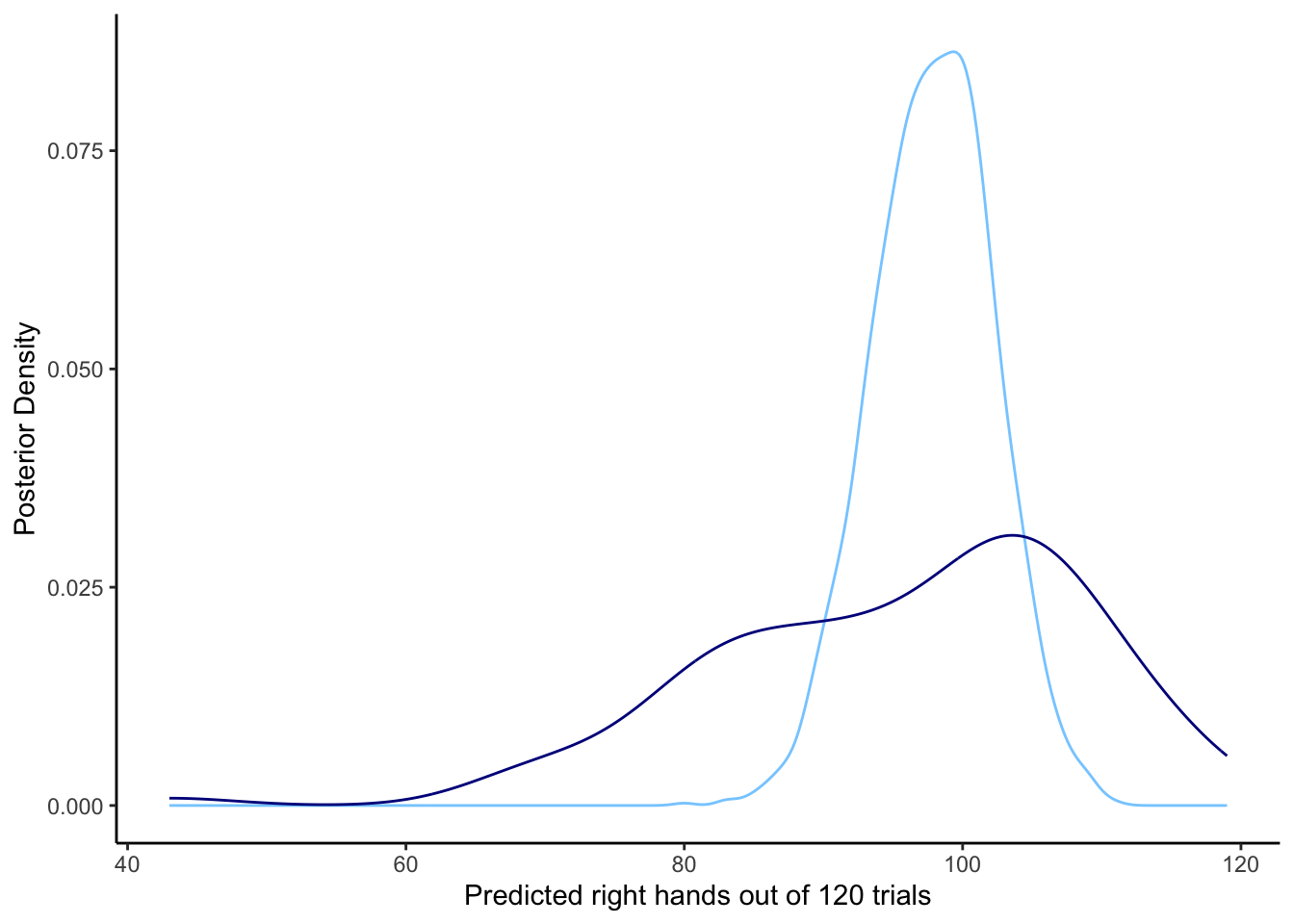
p1 <- ggplot(draws_df) +
geom_density(aes(preds1), color = "skyblue1", alpha = 0.3) +
geom_point(x = subset(d2, agent == 1)$right, y = 0, shape = 23, color = "darkblue", fill = "darkblue") +
theme_classic()
p2 <- ggplot(draws_df) +
geom_density(aes(preds11), color = "skyblue1", alpha = 0.3) +
geom_point(x = subset(d2, agent == 11)$right, y = 0, shape = 23, color = "darkblue", fill = "darkblue") +
theme_classic()
p3 <- ggplot(draws_df) +
geom_density(aes(preds21), color = "skyblue1", alpha = 0.3) +
geom_point(x = subset(d2, agent == 21)$right, y = 0, shape = 23, color = "darkblue", fill = "darkblue") +
theme_classic()
library(patchwork)
p1 + p2 + p3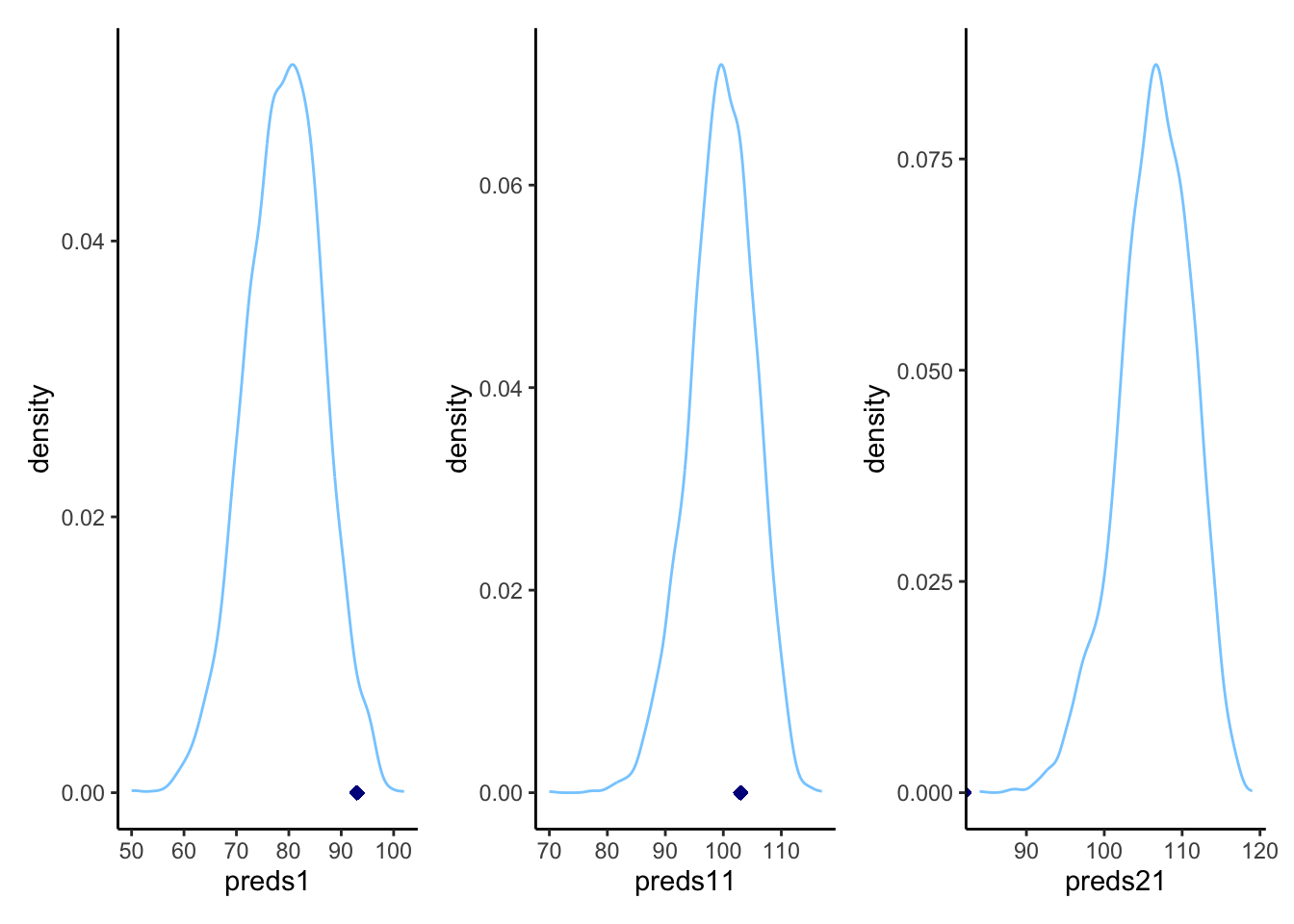
6.5.3 Multilevel memory
[MISSING: DAGS] [MISSING: EXPLAIN NEW STAN CODE] [MISSING: POP VS IND LEVEL PREDICTIONS]
Prep the data
## Create the data
d1 <- d %>%
subset(select = c(agent, memoryChoice)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = memoryChoice)
d2 <- d %>%
subset(select = c(agent, randomChoice)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = randomChoice)
data <- list(
trials = trials,
agents = agents,
h = as.matrix(d1[1:120,2:101]),
other = as.matrix(d2[1:120,2:101])
)Code, compile and fit the model
stan_model <- "
//
//
functions{
real normal_lb_rng(real mu, real sigma, real lb) {
real p = normal_cdf(lb | mu, sigma); // cdf for bounds
real u = uniform_rng(p, 1);
return (sigma * inv_Phi(u)) + mu; // inverse cdf for value
}
}
// The input (data) for the model.
data {
int<lower = 1> trials;
int<lower = 1> agents;
array[trials, agents] int h;
array[trials, agents] int other;
}
// The parameters accepted by the model.
parameters {
real biasM;
real<lower = 0> biasSD;
real betaM;
real<lower = 0> betaSD;
array[agents] real bias;
array[agents] real beta;
}
transformed parameters {
array[trials, agents] real memory;
for (agent in 1:agents){
for (trial in 1:trials){
if (trial == 1) {
memory[trial, agent] = 0.5;
}
if (trial < trials){
memory[trial + 1, agent] = memory[trial, agent] + ((other[trial, agent] - memory[trial, agent]) / trial);
if (memory[trial + 1, agent] == 0){memory[trial + 1, agent] = 0.01;}
if (memory[trial + 1, agent] == 1){memory[trial + 1, agent] = 0.99;}
}
}
}
}
// The model to be estimated.
model {
target += normal_lpdf(biasM | 0, 1);
target += normal_lpdf(biasSD | 0, .3) -
normal_lccdf(0 | 0, .3);
target += normal_lpdf(betaM | 0, .3);
target += normal_lpdf(betaSD | 0, .3) -
normal_lccdf(0 | 0, .3);
target += normal_lpdf(bias | biasM, biasSD);
target += normal_lpdf(beta | betaM, betaSD);
for (agent in 1:agents)
for (trial in 1:trials){
target += bernoulli_logit_lpmf(h[trial,agent] |
bias[agent] + logit(memory[trial, agent]) * (beta[agent]));
}
}
generated quantities{
real biasM_prior;
real<lower=0> biasSD_prior;
real betaM_prior;
real<lower=0> betaSD_prior;
real bias_prior;
real beta_prior;
int<lower=0, upper = trials> prior_preds0;
int<lower=0, upper = trials> prior_preds1;
int<lower=0, upper = trials> prior_preds2;
int<lower=0, upper = trials> posterior_preds0;
int<lower=0, upper = trials> posterior_preds1;
int<lower=0, upper = trials> posterior_preds2;
array[agents] int<lower=0, upper = trials> posterior_predsID0;
array[agents] int<lower=0, upper = trials> posterior_predsID1;
array[agents] int<lower=0, upper = trials> posterior_predsID2;
biasM_prior = normal_rng(0,1);
biasSD_prior = normal_lb_rng(0,0.3,0);
betaM_prior = normal_rng(0,1);
betaSD_prior = normal_lb_rng(0,0.3,0);
bias_prior = normal_rng(biasM_prior, biasSD_prior);
beta_prior = normal_rng(betaM_prior, betaSD_prior);
prior_preds0 = binomial_rng(trials, inv_logit(bias_prior + 0 * beta_prior));
prior_preds1 = binomial_rng(trials, inv_logit(bias_prior + 1 * beta_prior));
prior_preds2 = binomial_rng(trials, inv_logit(bias_prior + 2 * beta_prior));
posterior_preds0 = binomial_rng(trials, inv_logit(biasM + 0 * betaM));
posterior_preds1 = binomial_rng(trials, inv_logit(biasM + 1 * betaM));
posterior_preds2 = binomial_rng(trials, inv_logit(biasM + 2 * betaM));
for (agent in 1:agents){
posterior_predsID0[agent] = binomial_rng(trials, inv_logit(bias[agent] + 0 * beta[agent]));
posterior_predsID1[agent] = binomial_rng(trials, inv_logit(bias[agent] + 1 * beta[agent]));
posterior_predsID2[agent] = binomial_rng(trials, inv_logit(bias[agent] + 2 * beta[agent]));
}
}
"
write_stan_file(
stan_model,
dir = "stan/",
basename = "W5_MultilevelMemory.stan")
file <- file.path("stan/W5_MultilevelMemory.stan")
mod <- cmdstan_model(file,
cpp_options = list(stan_threads = TRUE),
stanc_options = list("O1"))
# The following command calls Stan with specific options.
samples <- mod$sample(
data = data,
seed = 123,
chains = 2,
parallel_chains = 2,
threads_per_chain = 2,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 500,
max_treedepth = 20,
adapt_delta = 0.99,
)
samples$save_object(file = "simmodels/W5_MultilevelMemory_centered.RDS")6.5.4 Assessing multilevel memory
## File /var/folders/lt/zspkqnxd5yg92kybm5f433_cfjr0d6/T/RtmpTP5vj3/W5_MultilevelMemory-202303101235-1-8e8f81.csv not found
## File /var/folders/lt/zspkqnxd5yg92kybm5f433_cfjr0d6/T/RtmpTP5vj3/W5_MultilevelMemory-202303101235-2-8e8f81.csv not found
## No valid input files, exiting.## # A tibble: 4 × 10
## variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 biasM 0.539 0.537 0.0872 0.0859 0.400 0.686 1.00 324. 718.
## 2 betaM 1.02 1.02 0.0700 0.0694 0.906 1.14 1.00 460. 1066.
## 3 biasSD 0.283 0.282 0.0672 0.0689 0.176 0.394 1.01 269. 277.
## 4 betaSD 0.410 0.407 0.0493 0.0499 0.332 0.494 1.00 1438. 2248.draws_df <- as_draws_df(samples$draws())
p1 <- ggplot(draws_df, aes(.iteration, biasM, group = .chain, color = .chain)) +
geom_line() +
theme_classic()
p2 <- ggplot(draws_df, aes(.iteration, biasSD, group = .chain, color = .chain)) +
geom_line() +
theme_classic()
p3 <- ggplot(draws_df, aes(.iteration, betaM, group = .chain, color = .chain)) +
geom_line() +
theme_classic()
p4 <- ggplot(draws_df, aes(.iteration, betaSD, group = .chain, color = .chain)) +
geom_line() +
theme_classic()
p1 + p2 + p3 + p4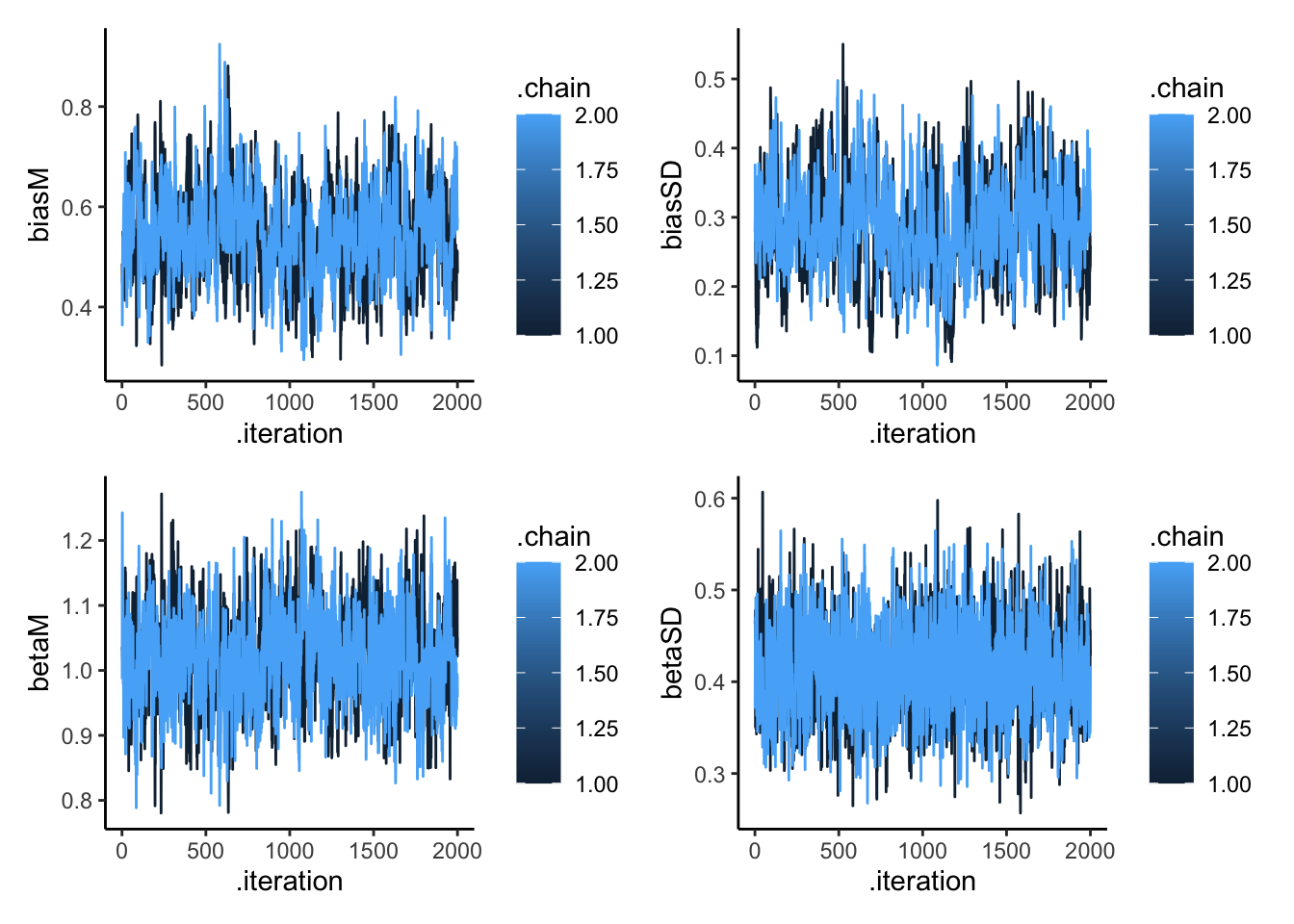
6.5.4.1 Predictive prior checks
##
ggplot(draws_df) +
geom_histogram(aes(`prior_preds0`), color = "darkblue", fill = "blue", alpha = 0.3) +
geom_histogram(aes(`prior_preds1`), color = "darkblue", fill = "green", alpha = 0.3) +
geom_histogram(aes(`prior_preds2`), color = "darkblue", fill = "red", alpha = 0.3) +
xlab("Predicted right hands out of 120 trials") +
ylab("Posterior Density") +
theme_classic()## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.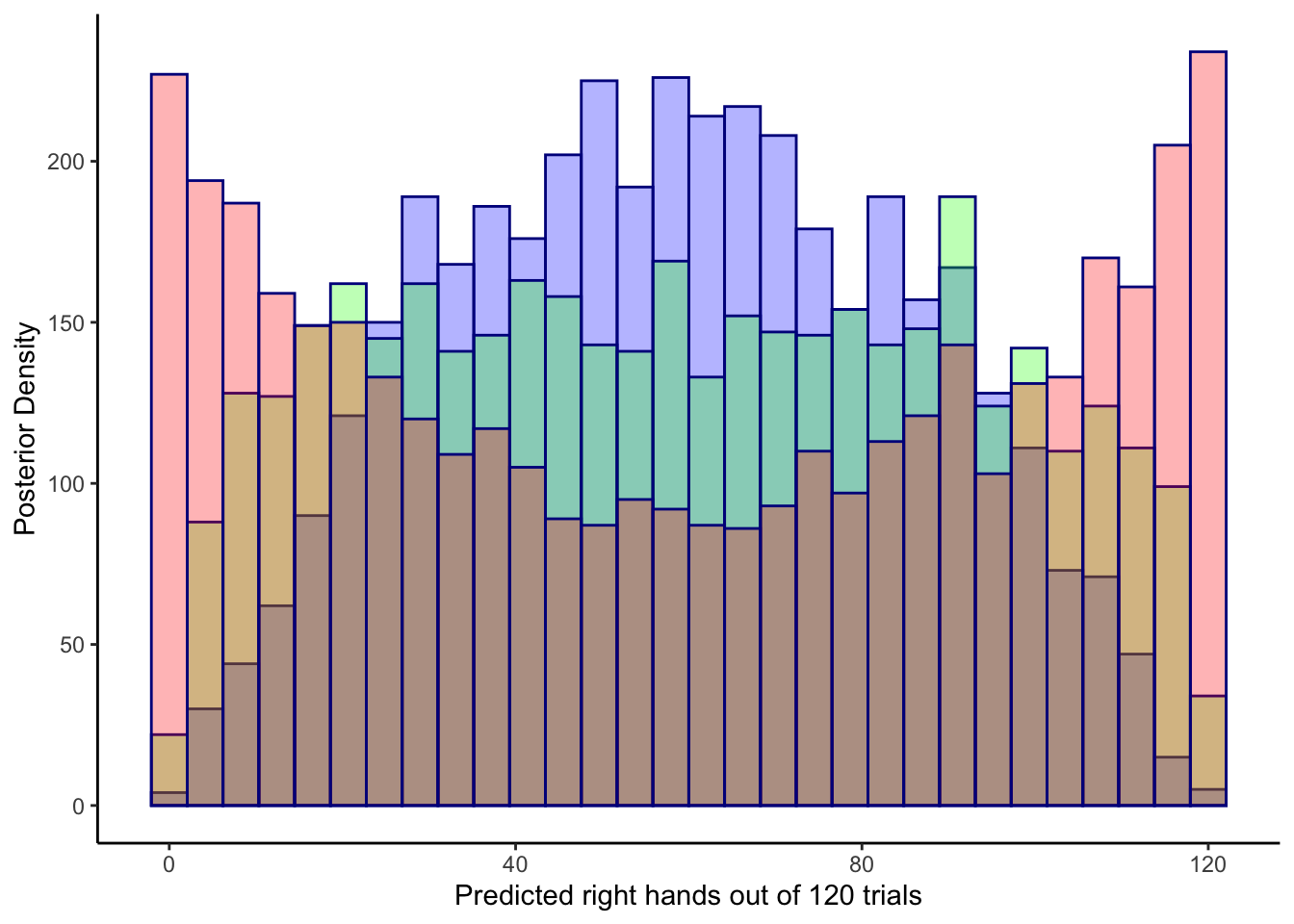
6.5.4.2 Prior posterior update checks
biasM <- 0 biasSD <- 0.1 betaM <- 1.5 betaSD <- 0.3
##
p1 <- ggplot(draws_df) +
geom_density(aes(biasM), fill = "blue", alpha = 0.3) +
geom_density(aes(biasM_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = 0) +
xlab("Mean bias") +
ylab("Posterior Density") +
theme_classic()
p2 <- ggplot(draws_df) +
geom_density(aes(biasSD), fill = "blue", alpha = 0.3) +
geom_density(aes(biasSD_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = 0.1) +
xlab("Variance of bias") +
ylab("Posterior Density") +
theme_classic()
p3 <- ggplot(draws_df) +
geom_density(aes(betaM), fill = "blue", alpha = 0.3) +
geom_density(aes(betaM_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = 1.5) +
xlab("Mean Beta") +
ylab("Posterior Density") +
theme_classic()
p4 <- ggplot(draws_df) +
geom_density(aes(betaSD), fill = "blue", alpha = 0.3) +
geom_density(aes(betaSD_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = 0.3) +
xlab("Variance of beta") +
ylab("Posterior Density") +
theme_classic()
p1 + p2 + p3 + p4 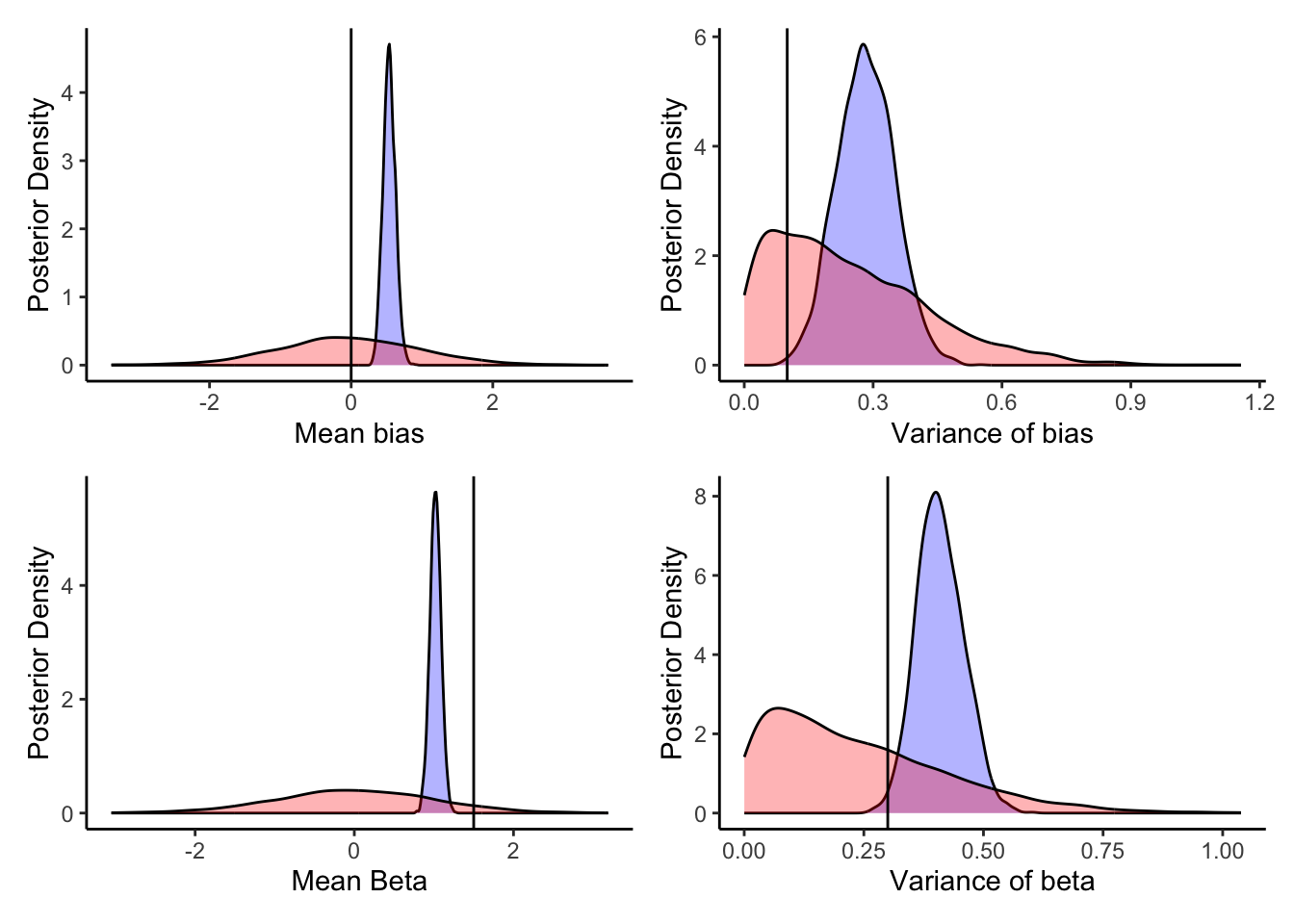
6.5.4.3 Posterior predictive checks
p1 <- ggplot(draws_df) +
geom_histogram(aes(`prior_preds0`), color = "darkblue", fill = "lightblue", alpha = 0.3) +
geom_histogram(aes(`posterior_preds0`), color = "darkblue", fill = "blue", alpha = 0.3) +
xlab("Predicted right hands out of 120 trials") +
ylab("Posterior Density") +
theme_classic()
p2 <- ggplot(draws_df) +
geom_histogram(aes(`prior_preds1`), color = "darkblue", fill = "lightblue", alpha = 0.3) +
geom_histogram(aes(`posterior_preds1`), color = "darkblue", fill = "blue", alpha = 0.3) +
xlab("Predicted right hands out of 120 trials") +
ylab("Posterior Density") +
theme_classic()
p3 <- ggplot(draws_df) +
geom_histogram(aes(`prior_preds2`), color = "darkblue", fill = "lightblue", alpha = 0.3) +
geom_histogram(aes(`posterior_preds2`), color = "darkblue", fill = "blue", alpha = 0.3) +
xlab("Predicted right hands out of 120 trials") +
ylab("Posterior Density") +
theme_classic()
p1 + p2 + p3## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.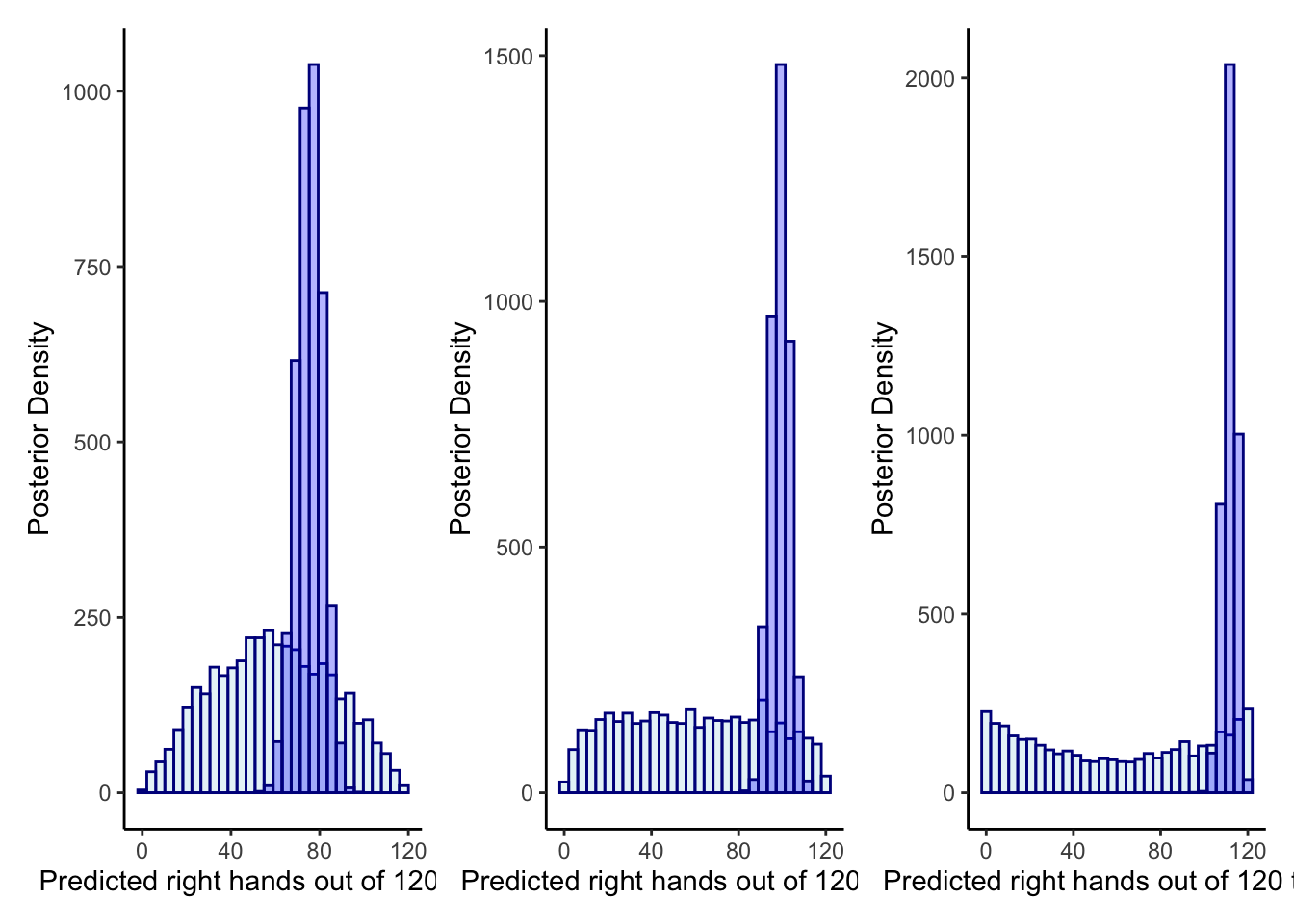
p1 <- ggplot(draws_df, aes(biasM, biasSD, group = .chain, color = .chain)) +
geom_point(alpha = 0.1) +
theme_classic()
p2 <- ggplot(draws_df, aes(betaM, betaSD, group = .chain, color = .chain)) +
geom_point(alpha = 0.1) +
theme_classic()
p3 <- ggplot(draws_df, aes(biasM, betaM, group = .chain, color = .chain)) +
geom_point(alpha = 0.1) +
theme_classic()
p4 <- ggplot(draws_df, aes(biasSD, betaSD, group = .chain, color = .chain)) +
geom_point(alpha = 0.1) +
theme_classic()
p1 + p2 + p3 + p4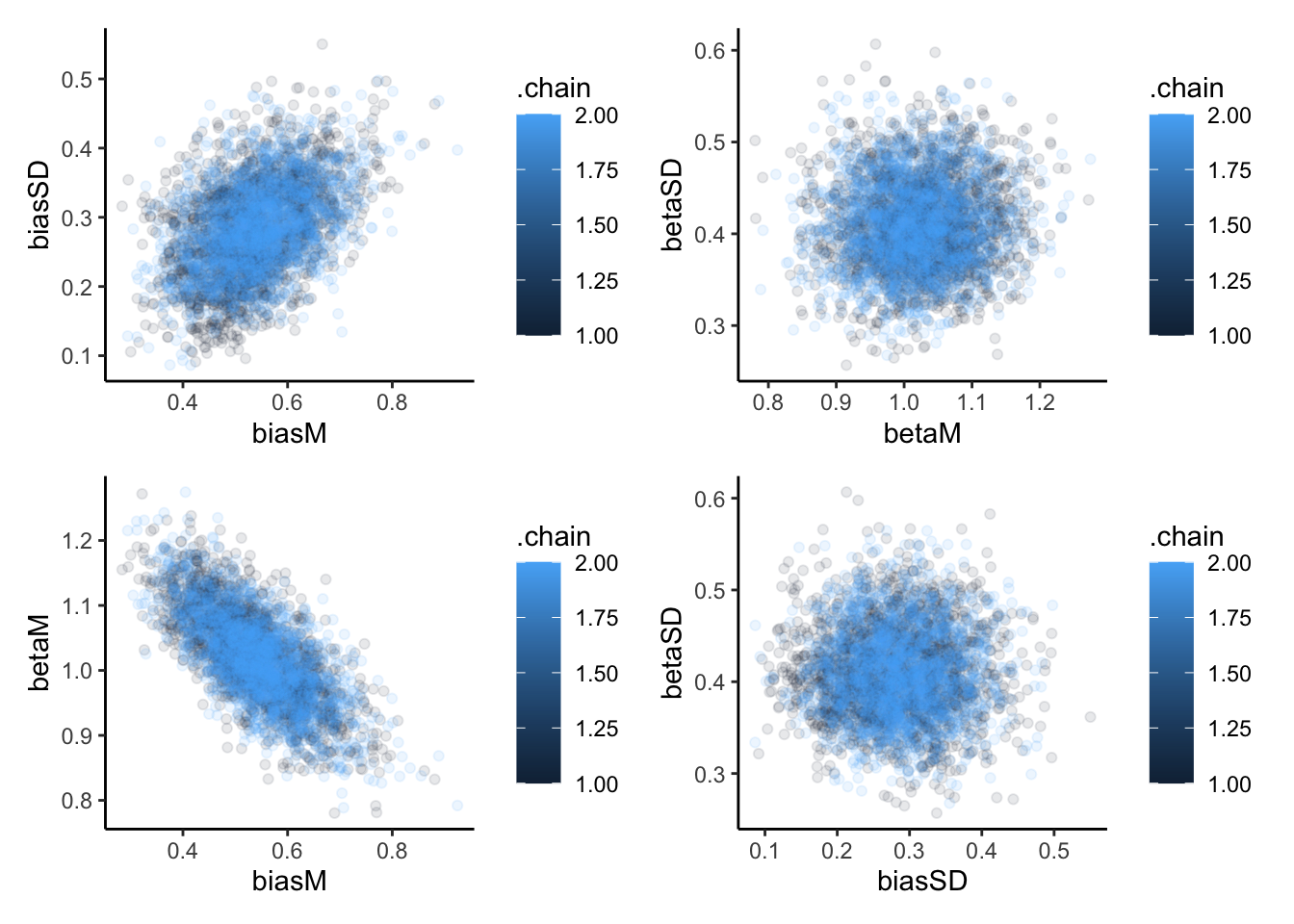
6.5.5 Multilevel memory with non centered parameterization
Prep the data
## Create the data
d1 <- d %>%
subset(select = c(agent, memoryChoice)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = memoryChoice)
d2 <- d %>%
subset(select = c(agent, randomChoice)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = randomChoice)
data <- list(
trials = trials,
agents = agents,
h = as.matrix(d1[1:120,2:101]),
other = as.matrix(d2[1:120,2:101])
)Code, compile and and fit the model
## NON-CENTERED PARAMETRIZATION
stan_model_nc <- "
//
// This STAN model is a multilevel memory agent
//
functions{
real normal_lb_rng(real mu, real sigma, real lb) {
real p = normal_cdf(lb | mu, sigma); // cdf for bounds
real u = uniform_rng(p, 1);
return (sigma * inv_Phi(u)) + mu; // inverse cdf for value
}
}
// The input (data) for the model.
data {
int<lower = 1> trials;
int<lower = 1> agents;
array[trials, agents] int h;
array[trials, agents] int other;
}
// The parameters accepted by the model.
parameters {
real biasM;
real<lower = 0> biasSD;
real betaM;
real<lower = 0> betaSD;
vector[agents] biasID_z;
vector[agents] betaID_z;
}
transformed parameters {
array[trials, agents] real memory;
vector[agents] biasID;
vector[agents] betaID;
for (agent in 1:agents){
for (trial in 1:trials){
if (trial == 1) {
memory[trial, agent] = 0.5;
}
if (trial < trials){
memory[trial + 1, agent] = memory[trial, agent] + ((other[trial, agent] - memory[trial, agent]) / trial);
if (memory[trial + 1, agent] == 0){memory[trial + 1, agent] = 0.01;}
if (memory[trial + 1, agent] == 1){memory[trial + 1, agent] = 0.99;}
}
}
}
biasID = biasID_z * biasSD;
betaID = betaID_z * betaSD;
}
// The model to be estimated.
model {
target += normal_lpdf(biasM | 0, 1);
target += normal_lpdf(biasSD | 0, .3) -
normal_lccdf(0 | 0, .3);
target += normal_lpdf(betaM | 0, .3);
target += normal_lpdf(betaSD | 0, .3) -
normal_lccdf(0 | 0, .3);
target += std_normal_lpdf(to_vector(biasID_z)); // target += normal_lpdf(to_vector(biasID_z) | 0, 1);
target += std_normal_lpdf(to_vector(betaID_z)); // target += normal_lpdf(to_vector(betaID_z) | 0, 1);
for (agent in 1:agents){
for (trial in 1:trials){
target += bernoulli_logit_lpmf(h[trial,agent] |
biasM + biasID[agent] + logit(memory[trial, agent]) * (betaM + betaID[agent]));
}
}
}
generated quantities{
real biasM_prior;
real<lower=0> biasSD_prior;
real betaM_prior;
real<lower=0> betaSD_prior;
real bias_prior;
real beta_prior;
array[agents] int<lower=0, upper = trials> prior_preds0;
array[agents] int<lower=0, upper = trials> prior_preds1;
array[agents] int<lower=0, upper = trials> prior_preds2;
array[agents] int<lower=0, upper = trials> posterior_preds0;
array[agents] int<lower=0, upper = trials> posterior_preds1;
array[agents] int<lower=0, upper = trials> posterior_preds2;
biasM_prior = normal_rng(0,1);
biasSD_prior = normal_lb_rng(0,0.3,0);
betaM_prior = normal_rng(0,1);
betaSD_prior = normal_lb_rng(0,0.3,0);
bias_prior = normal_rng(biasM_prior, biasSD_prior);
beta_prior = normal_rng(betaM_prior, betaSD_prior);
for (agent in 1:agents){
prior_preds0[agent] = binomial_rng(trials, inv_logit(bias_prior + 0 * beta_prior));
prior_preds1[agent] = binomial_rng(trials, inv_logit(bias_prior + 1 * beta_prior));
prior_preds2[agent] = binomial_rng(trials, inv_logit(bias_prior + 2 * beta_prior));
posterior_preds0[agent] = binomial_rng(trials, inv_logit(biasM + biasID[agent] + 0 * (betaM + betaID[agent])));
posterior_preds1[agent] = binomial_rng(trials, inv_logit(biasM + biasID[agent] + 1 * (betaM + betaID[agent])));
posterior_preds2[agent] = binomial_rng(trials, inv_logit(biasM + biasID[agent] + 2 * (betaM + betaID[agent])));
}
}
"
write_stan_file(
stan_model_nc,
dir = "stan/",
basename = "W5_MultilevelMemory_nc.stan")
file <- file.path("stan/W5_MultilevelMemory_nc.stan")
mod_nc <- cmdstan_model(file,
cpp_options = list(stan_threads = TRUE),
stanc_options = list("O1"))
# The following command calls Stan with specific options.
samples <- mod_nc$sample(
data = data,
seed = 123,
chains = 2,
parallel_chains = 2,
threads_per_chain = 2,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 500,
max_treedepth = 20,
adapt_delta = 0.99,
)
samples$save_object(file = "simmodels/W5_MultilevelMemory_noncentered.RDS")6.5.6 Assessing multilevel memory
## File /var/folders/lt/zspkqnxd5yg92kybm5f433_cfjr0d6/T/RtmpTP5vj3/W5_MultilevelMemory_nc-202303101250-1-612dbb.csv not found
## File /var/folders/lt/zspkqnxd5yg92kybm5f433_cfjr0d6/T/RtmpTP5vj3/W5_MultilevelMemory_nc-202303101250-2-612dbb.csv not found
## No valid input files, exiting.## # A tibble: 4 × 10
## variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 biasM 0.538 0.537 0.0870 0.0875 0.397 0.683 1.00 1315. 2025.
## 2 betaM 1.02 1.02 0.0726 0.0732 0.901 1.14 1.00 1187. 2168.
## 3 biasSD 0.281 0.281 0.0702 0.0698 0.168 0.401 1.00 630. 956.
## 4 betaSD 0.411 0.409 0.0497 0.0493 0.333 0.499 1.00 1394. 2137.draws_df <- as_draws_df(samples$draws())
p1 <- ggplot(draws_df, aes(.iteration, biasM, group = .chain, color = .chain)) +
geom_line() +
theme_classic()
p2 <- ggplot(draws_df, aes(.iteration, biasSD, group = .chain, color = .chain)) +
geom_line() +
theme_classic()
p3 <- ggplot(draws_df, aes(.iteration, betaM, group = .chain, color = .chain)) +
geom_line() +
theme_classic()
p4 <- ggplot(draws_df, aes(.iteration, betaSD, group = .chain, color = .chain)) +
geom_line() +
theme_classic()
p1 + p2 + p3 + p4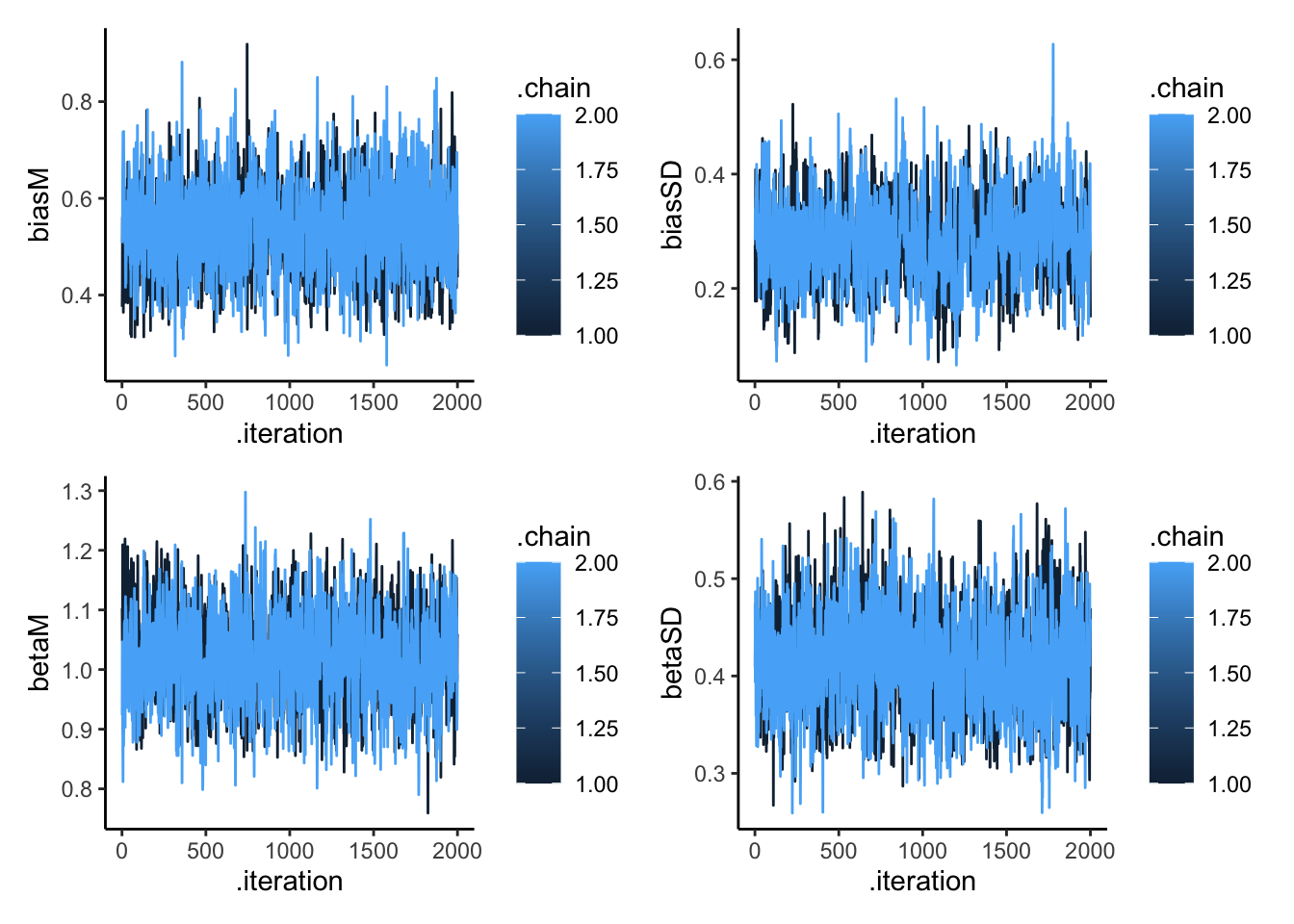
6.5.6.1 Predictive prior checks
##
ggplot(draws_df) +
geom_histogram(aes(`prior_preds0[1]`), color = "darkblue", fill = "blue", alpha = 0.3) +
geom_histogram(aes(`prior_preds1[1]`), color = "darkblue", fill = "green", alpha = 0.3) +
geom_histogram(aes(`prior_preds2[1]`), color = "darkblue", fill = "red", alpha = 0.3) +
xlab("Predicted right hands out of 120 trials") +
ylab("Posterior Density") +
theme_classic()## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.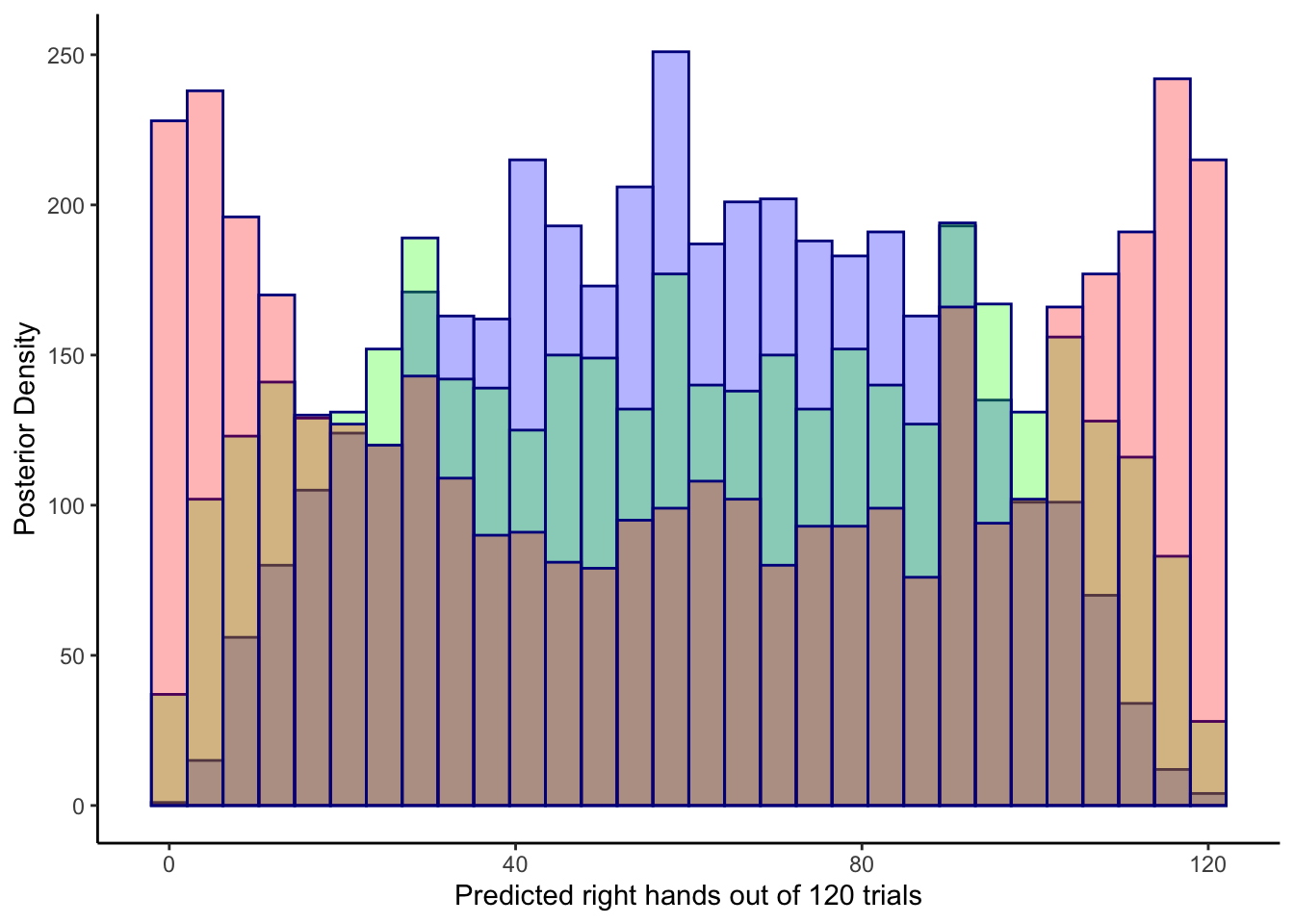
6.5.6.2 Prior posterior update checks
biasM <- 0 biasSD <- 0.1 betaM <- 1.5 betaSD <- 0.3
##
p1 <- ggplot(draws_df) +
geom_density(aes(logit_scaled(biasM)), fill = "blue", alpha = 0.3) +
geom_density(aes(biasM_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = 0) +
xlab("Mean bias") +
ylab("Posterior Density") +
theme_classic()
p2 <- ggplot(draws_df) +
geom_density(aes(biasSD), fill = "blue", alpha = 0.3) +
geom_density(aes(biasSD_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = 0.1) +
xlab("Variance of bias") +
ylab("Posterior Density") +
theme_classic()
p3 <- ggplot(draws_df) +
geom_density(aes(betaM), fill = "blue", alpha = 0.3) +
geom_density(aes(betaM_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = 1.5) +
xlab("Mean Beta") +
ylab("Posterior Density") +
theme_classic()
p4 <- ggplot(draws_df) +
geom_density(aes(betaSD), fill = "blue", alpha = 0.3) +
geom_density(aes(betaSD_prior), fill = "red", alpha = 0.3) +
geom_vline(xintercept = 0.3) +
xlab("Variance of beta") +
ylab("Posterior Density") +
theme_classic()
p1 + p2 + p3 + p4 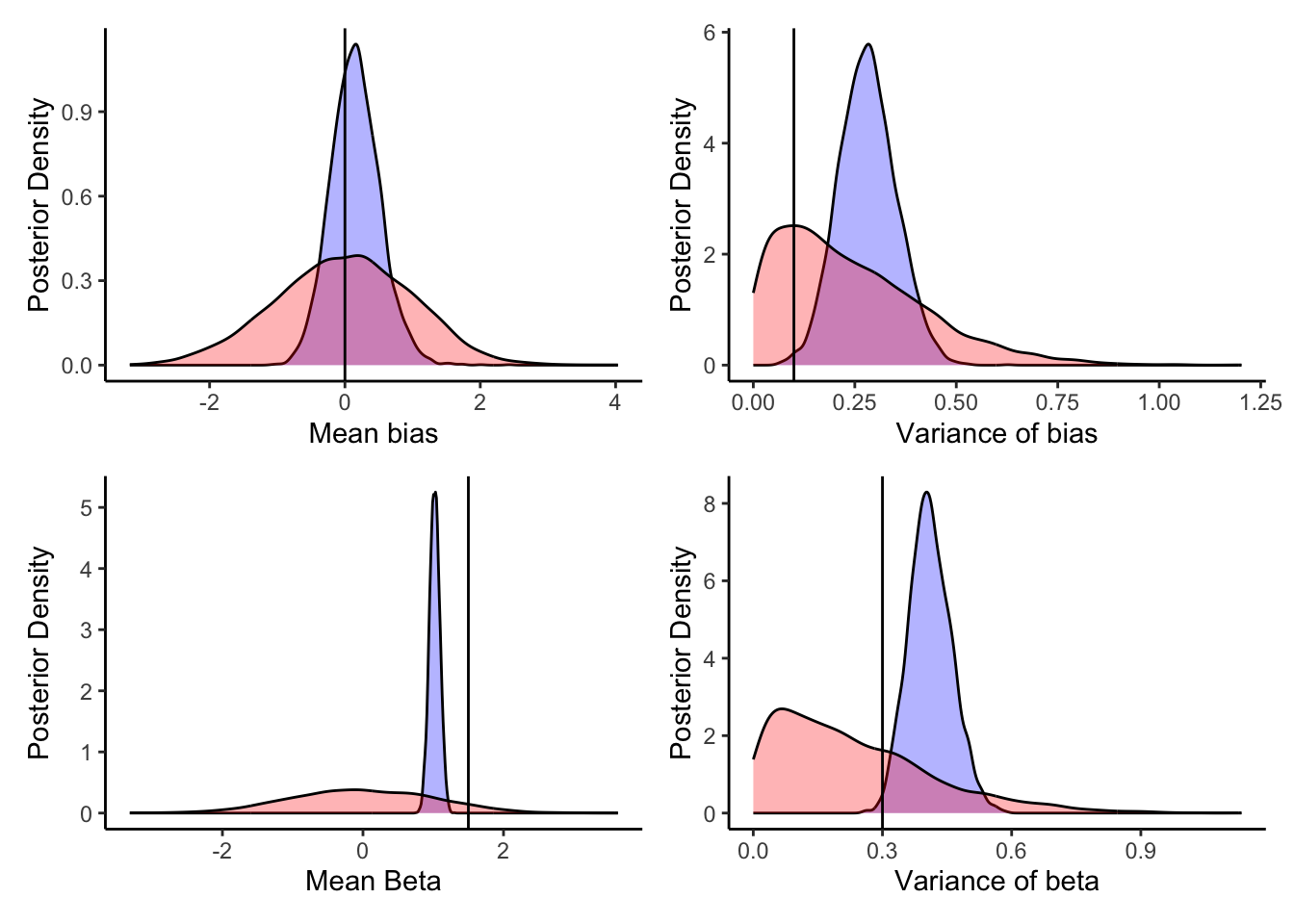
6.5.6.3 Posterior predictive checks
p1 <- ggplot(draws_df) +
geom_histogram(aes(`prior_preds0[1]`), color = "darkblue", fill = "lightblue", alpha = 0.3) +
geom_histogram(aes(`posterior_preds0[1]`), color = "darkblue", fill = "blue", alpha = 0.3) +
xlab("Predicted right hands out of 120 trials") +
ylab("Posterior Density") +
theme_classic()
p2 <- ggplot(draws_df) +
geom_histogram(aes(`prior_preds1[1]`), color = "darkblue", fill = "lightblue", alpha = 0.3) +
geom_histogram(aes(`posterior_preds1[1]`), color = "darkblue", fill = "blue", alpha = 0.3) +
xlab("Predicted right hands out of 120 trials") +
ylab("Posterior Density") +
theme_classic()
p3 <- ggplot(draws_df) +
geom_histogram(aes(`prior_preds2[1]`), color = "darkblue", fill = "lightblue", alpha = 0.3) +
geom_histogram(aes(`posterior_preds2[1]`), color = "darkblue", fill = "blue", alpha = 0.3) +
xlab("Predicted right hands out of 120 trials") +
ylab("Posterior Density") +
theme_classic()
p1 + p2 + p3## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.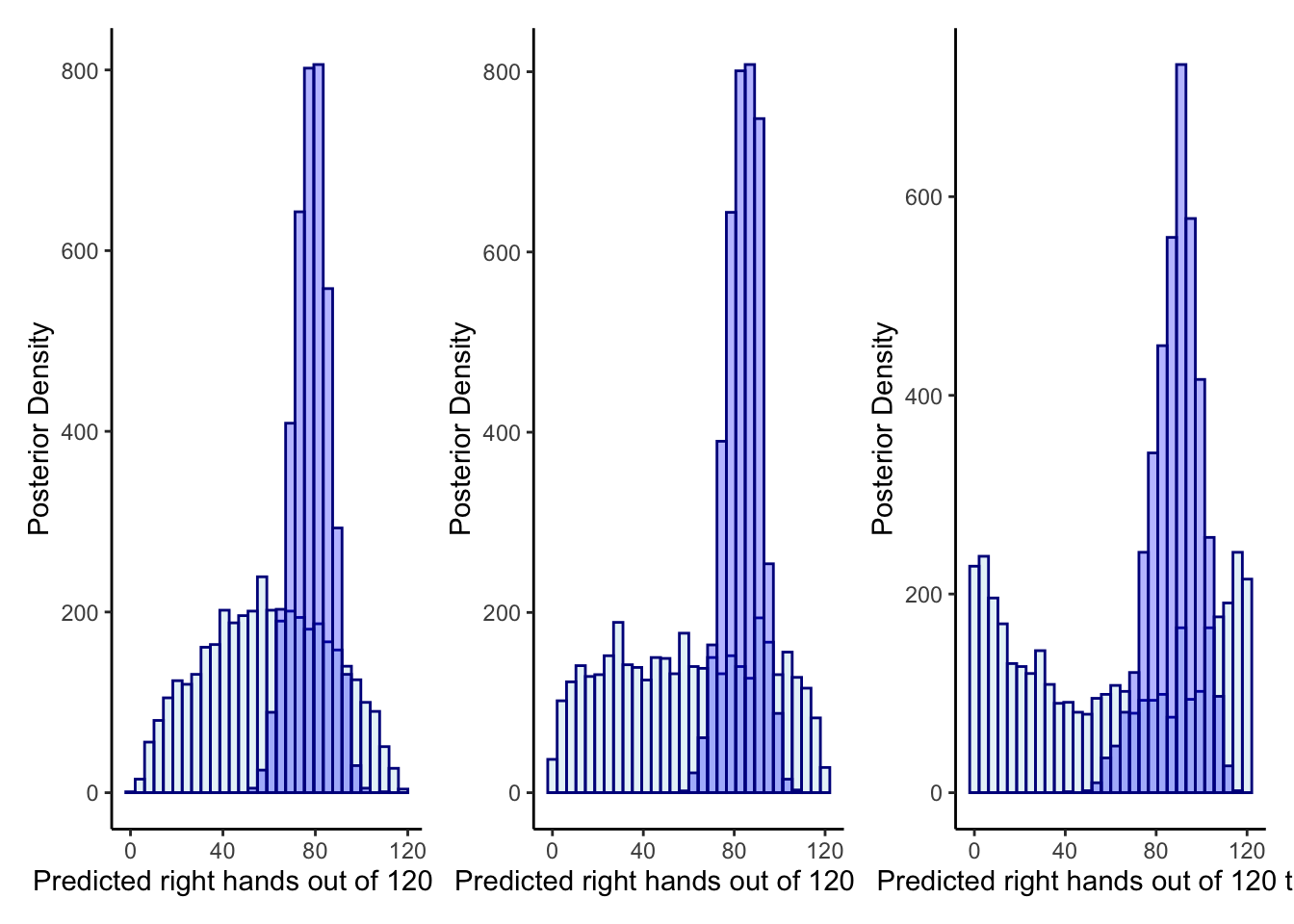
p1 <- ggplot(draws_df, aes(biasM, biasSD, group = .chain, color = .chain)) +
geom_point(alpha = 0.1) +
theme_classic()
p2 <- ggplot(draws_df, aes(betaM, betaSD, group = .chain, color = .chain)) +
geom_point(alpha = 0.1) +
theme_classic()
p3 <- ggplot(draws_df, aes(biasM, betaM, group = .chain, color = .chain)) +
geom_point(alpha = 0.1) +
theme_classic()
p4 <- ggplot(draws_df, aes(biasSD, betaSD, group = .chain, color = .chain)) +
geom_point(alpha = 0.1) +
theme_classic()
p1 + p2 + p3 + p4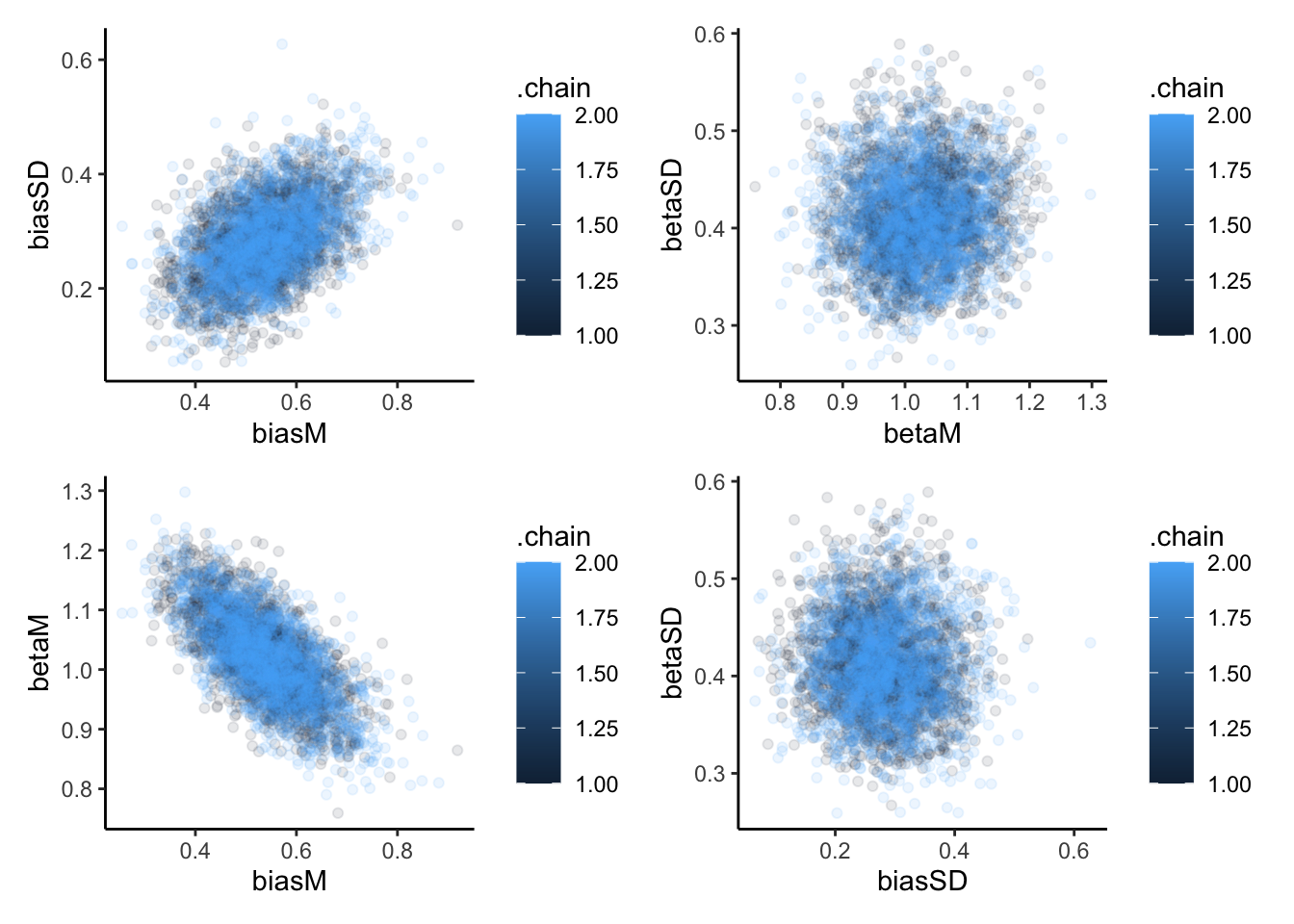
ggplot(draws_df) +
geom_density(aes(inv_logit_scaled(`biasID[1]`)), fill = "blue", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`biasID[15]`)), fill = "green", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`biasID[21]`)), fill = "lightblue", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`biasID[31]`)), fill = "darkblue", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`biasID[41]`)), fill = "yellow", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`biasID[51]`)), fill = "darkgreen", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`biasID[61]`)), fill = "lightgreen", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(biasM_prior)), fill = "pink", alpha = 0.3) +
geom_density(aes(bias_prior), fill = "purple", alpha = 0.3) +
xlab("Bias parameter") +
ylab("Posterior Density") +
theme_classic()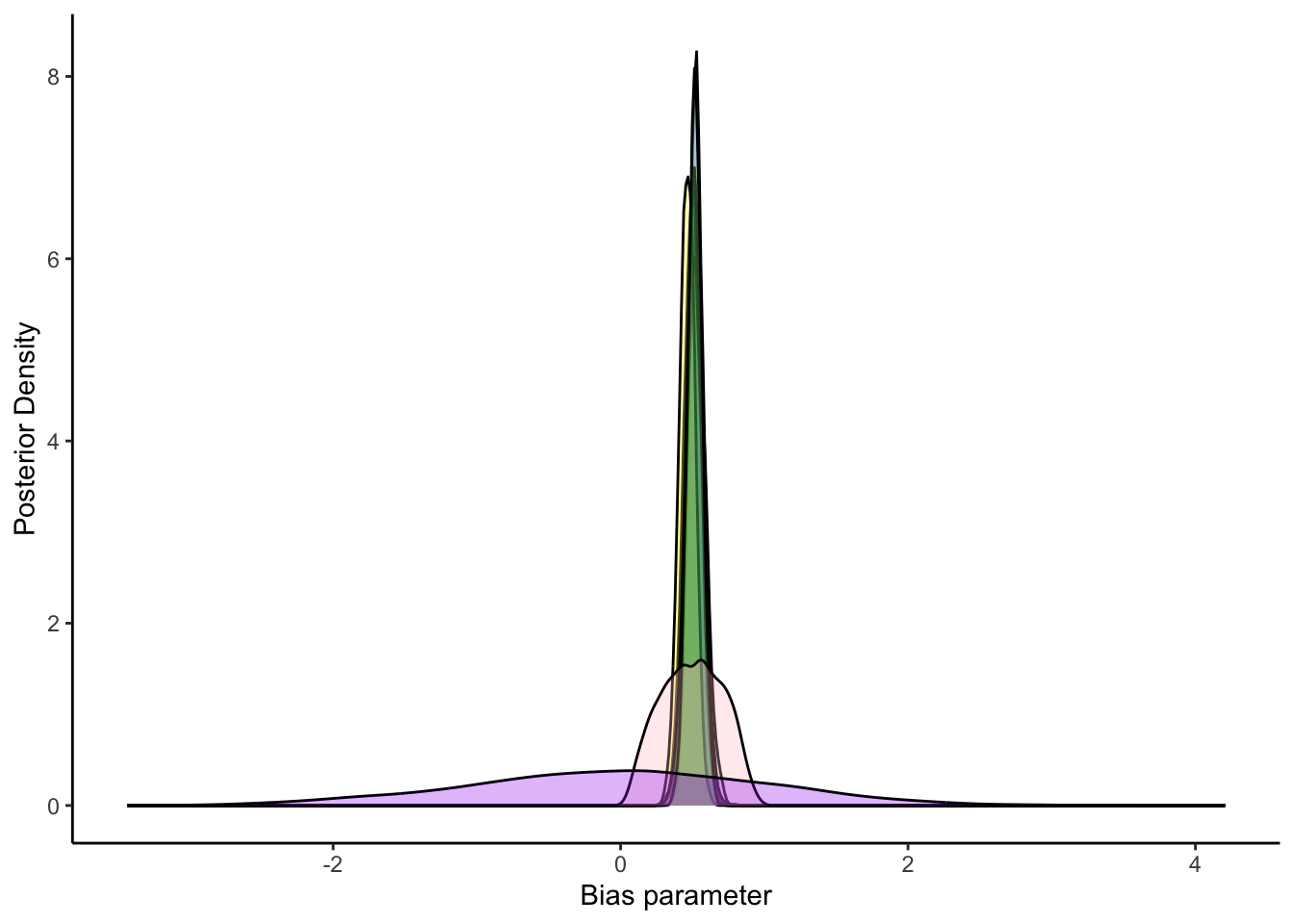
ggplot(draws_df) +
geom_density(aes(inv_logit_scaled(`betaID[1]`)), fill = "blue", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`betaID[15]`)), fill = "green", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`betaID[21]`)), fill = "lightblue", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`betaID[31]`)), fill = "darkblue", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`betaID[41]`)), fill = "yellow", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`betaID[51]`)), fill = "darkgreen", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(`betaID[61]`)), fill = "lightgreen", alpha = 0.3) +
geom_density(aes(inv_logit_scaled(betaM_prior)), fill = "pink", alpha = 0.3) +
geom_density(aes(beta_prior), fill = "purple", alpha = 0.3) +
xlab("Beta parameter") +
ylab("Posterior Density") +
theme_classic()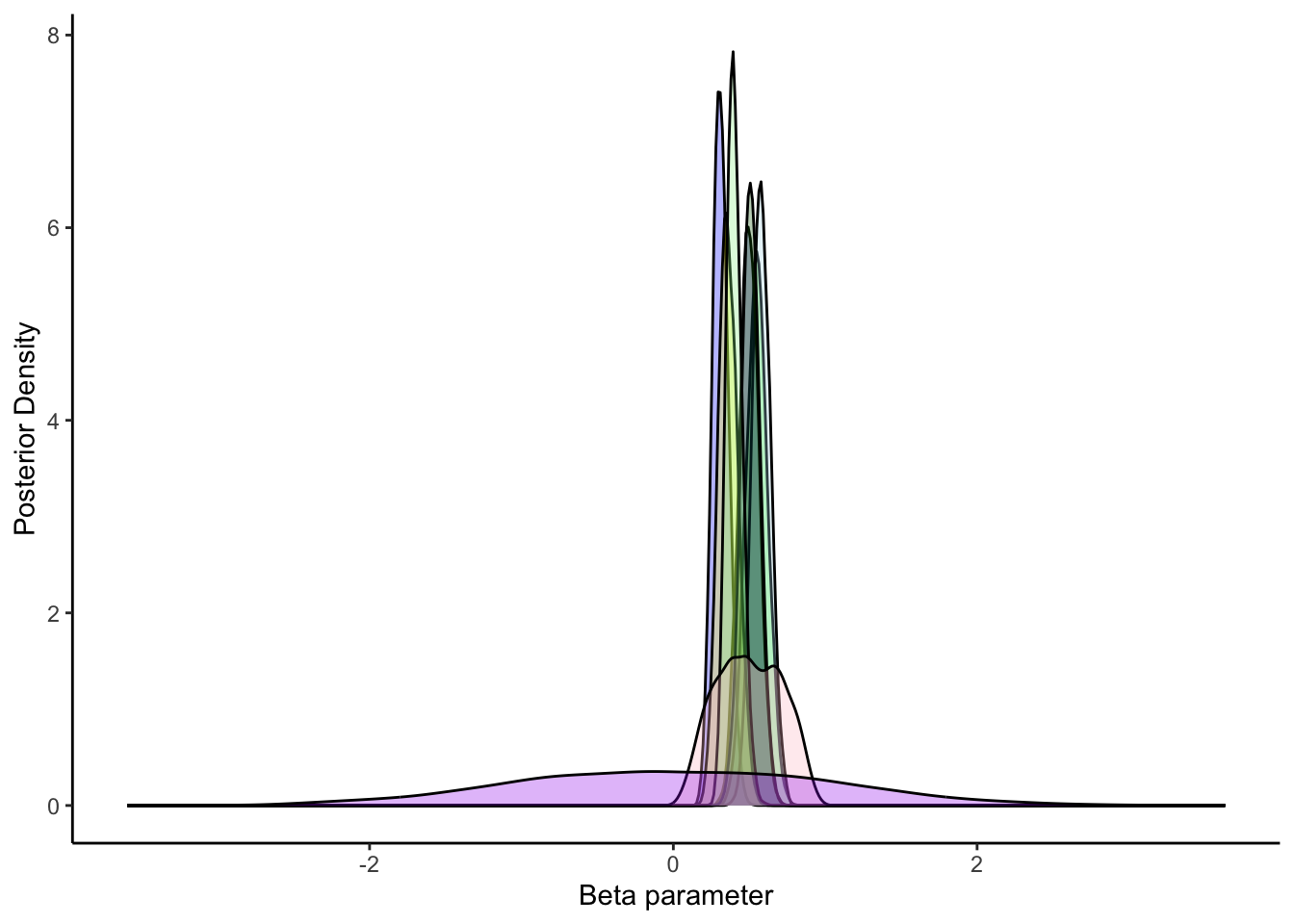
6.5.7 Multilevel memory with correlation between parameters
stan_model_nc_cor <- "
//
// This STAN model infers a random bias from a sequences of 1s and 0s (heads and tails)
//
functions{
real normal_lb_rng(real mu, real sigma, real lb) {
real p = normal_cdf(lb | mu, sigma); // cdf for bounds
real u = uniform_rng(p, 1);
return (sigma * inv_Phi(u)) + mu; // inverse cdf for value
}
}
// The input (data) for the model.
data {
int<lower = 1> trials;
int<lower = 1> agents;
array[trials, agents] int h;
array[trials, agents] int other;
}
// The parameters accepted by the model.
parameters {
real biasM;
real betaM;
vector<lower = 0>[2] tau;
matrix[2, agents] z_IDs;
cholesky_factor_corr[2] L_u;
}
transformed parameters {
array[trials, agents] real memory;
matrix[agents,2] IDs;
IDs = (diag_pre_multiply(tau, L_u) * z_IDs)';
for (agent in 1:agents){
for (trial in 1:trials){
if (trial == 1) {
memory[trial, agent] = 0.5;
}
if (trial < trials){
memory[trial + 1, agent] = memory[trial, agent] + ((other[trial, agent] - memory[trial, agent]) / trial);
if (memory[trial + 1, agent] == 0){memory[trial + 1, agent] = 0.01;}
if (memory[trial + 1, agent] == 1){memory[trial + 1, agent] = 0.99;}
}
}
}
}
// The model to be estimated.
model {
target += normal_lpdf(biasM | 0, 1);
target += normal_lpdf(tau[1] | 0, .3) -
normal_lccdf(0 | 0, .3);
target += normal_lpdf(betaM | 0, .3);
target += normal_lpdf(tau[2] | 0, .3) -
normal_lccdf(0 | 0, .3);
target += lkj_corr_cholesky_lpdf(L_u | 2);
target += std_normal_lpdf(to_vector(z_IDs));
for (agent in 1:agents){
for (trial in 1:trials){
target += bernoulli_logit_lpmf(h[trial, agent] | biasM + IDs[agent, 1] + memory[trial, agent] * (betaM + IDs[agent, 2]));
}
}
}
generated quantities{
real biasM_prior;
real<lower=0> biasSD_prior;
real betaM_prior;
real<lower=0> betaSD_prior;
real bias_prior;
real beta_prior;
array[agents] int<lower=0, upper = trials> prior_preds0;
array[agents] int<lower=0, upper = trials> prior_preds1;
array[agents] int<lower=0, upper = trials> prior_preds2;
array[agents] int<lower=0, upper = trials> posterior_preds0;
array[agents] int<lower=0, upper = trials> posterior_preds1;
array[agents] int<lower=0, upper = trials> posterior_preds2;
biasM_prior = normal_rng(0,1);
biasSD_prior = normal_lb_rng(0,0.3,0);
betaM_prior = normal_rng(0,1);
betaSD_prior = normal_lb_rng(0,0.3,0);
bias_prior = normal_rng(biasM_prior, biasSD_prior);
beta_prior = normal_rng(betaM_prior, betaSD_prior);
for (i in 1:agents){
prior_preds0[i] = binomial_rng(trials, inv_logit(bias_prior + 0 * beta_prior));
prior_preds1[i] = binomial_rng(trials, inv_logit(bias_prior + 1 * beta_prior));
prior_preds2[i] = binomial_rng(trials, inv_logit(bias_prior + 2 * beta_prior));
posterior_preds0[i] = binomial_rng(trials, inv_logit(biasM + IDs[i,1] + 0 * (betaM + IDs[i,2])));
posterior_preds1[i] = binomial_rng(trials, inv_logit(biasM + IDs[i,1] + 1 * (betaM + IDs[i,2])));
posterior_preds2[i] = binomial_rng(trials, inv_logit(biasM + IDs[i,1] + 2 * (betaM + IDs[i,2])));
}
}
"
write_stan_file(
stan_model_nc_cor,
dir = "stan/",
basename = "W5_MultilevelMemory_nc_cor.stan")
file <- file.path("stan/W5_MultilevelMemory_nc_cor.stan")
mod <- cmdstan_model(file, cpp_options = list(stan_threads = TRUE),
stanc_options = list("O1"))
# The following command calls Stan with specific options.
samples <- mod$sample(
data = data,
seed = 123,
chains = 2,
parallel_chains = 2,
threads_per_chain = 2,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 500,
max_treedepth = 20,
adapt_delta = 0.99,
)
samples$save_object(file = "simmodels/Memory_noncentered_corr.RDS")6.5.8 Assessing multilevel memory
[MISSING LOTS OF EVALUATION]
## File /var/folders/lt/zspkqnxd5yg92kybm5f433_cfjr0d6/T/RtmpTP5vj3/W5_MultilevelMemory_nc_cor-202303100657-1-969904.csv not found
## File /var/folders/lt/zspkqnxd5yg92kybm5f433_cfjr0d6/T/RtmpTP5vj3/W5_MultilevelMemory_nc_cor-202303100657-2-969904.csv not found
## No valid input files, exiting.6.5.9 Multilevel memory no pooling
[MISSING: EXPLANATION OF NO POOLING]
stan_model <- "
// The input (data) for the model. n of trials and h of heads
data {
int<lower = 1> trials;
int<lower = 1> agents;
array[trials, agents] int h;
array[trials, agents] int other;
}
// The parameters accepted by the model.
parameters {
array[trials] real bias;
array[trials] real beta;
}
transformed parameters {
array[trials, agents] real memory;
for (agent in 1:agents){
for (trial in 1:trials){
if (trial == 1) {
memory[trial, agent] = 0.5;
}
if (trial < trials){
memory[trial + 1, agent] = memory[trial, agent] + ((other[trial, agent] - memory[trial, agent]) / trial);
if (memory[trial + 1, agent] == 0){memory[trial + 1, agent] = 0.01;}
if (memory[trial + 1, agent] == 1){memory[trial + 1, agent] = 0.99;}
}
}
}
}
// The model to be estimated.
model {
target += normal_lpdf(bias | 0, 1);
target += normal_lpdf(beta | 0, 1);
for (agent in 1:agents){
for (trial in 1:trials){
target += bernoulli_logit_lpmf(h[trial, agent] | bias[agent] + memory[trial, agent] * (beta[agent]));
}
}
}
generated quantities{
real bias_prior;
real beta_prior;
int<lower=0, upper = trials> prior_preds0;
int<lower=0, upper = trials> prior_preds1;
int<lower=0, upper = trials> prior_preds2;
array[agents] int<lower=0, upper = trials> posterior_preds0;
array[agents] int<lower=0, upper = trials> posterior_preds1;
array[agents] int<lower=0, upper = trials> posterior_preds2;
bias_prior = normal_rng(0,1);
beta_prior = normal_rng(0,1);
prior_preds0 = binomial_rng(trials, inv_logit(bias_prior + 0 * beta_prior));
prior_preds1 = binomial_rng(trials, inv_logit(bias_prior + 1 * beta_prior));
prior_preds2 = binomial_rng(trials, inv_logit(bias_prior + 2 * beta_prior));
for (i in 1:agents){
posterior_preds0[i] = binomial_rng(trials, inv_logit(bias[i] + 0 * (beta[i])));
posterior_preds1[i] = binomial_rng(trials, inv_logit(bias[i] + 1 * (beta[i])));
posterior_preds2[i] = binomial_rng(trials, inv_logit(bias[i] + 2 * (beta[i])));
}
}
"
write_stan_file(
stan_model,
dir = "stan/",
basename = "W5_MultilevelMemory_nopooling.stan")
file <- file.path("stan/W5_MultilevelMemory_nopooling.stan")
mod <- cmdstan_model(file, cpp_options = list(stan_threads = TRUE),
stanc_options = list("O1"))
# The following command calls Stan with specific options.
samples <- mod$sample(
data = data,
seed = 123,
chains = 2,
parallel_chains = 2,
threads_per_chain = 2,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 500,
max_treedepth = 20,
adapt_delta = 0.99,
)
samples$save_object(file = "simmodels/W5_MultilevelMemory_nopooling.RDS")[MISSING: Evaluation of NO POOLING]
6.6 Multilevel full pooling
[MISSING: EXPLANATION OF FULL POOLING]
stan_model <- "
// The input (data) for the model. n of trials and h of heads
data {
int<lower = 1> trials;
int<lower = 1> agents;
array[trials, agents] int h;
array[trials, agents] int other;
}
// The parameters accepted by the model.
parameters {
real bias;
real beta;
}
transformed parameters {
array[trials, agents] real memory;
for (agent in 1:agents){
for (trial in 1:trials){
if (trial == 1) {
memory[trial, agent] = 0.5;
}
if (trial < trials){
memory[trial + 1, agent] = memory[trial, agent] + ((other[trial, agent] - memory[trial, agent]) / trial);
if (memory[trial + 1, agent] == 0){memory[trial + 1, agent] = 0.01;}
if (memory[trial + 1, agent] == 1){memory[trial + 1, agent] = 0.99;}
}
}
}
}
// The model to be estimated.
model {
target += normal_lpdf(bias | 0, 1);
target += normal_lpdf(beta | 0, 1);
for (agent in 1:agents){
for (trial in 1:trials){
target += bernoulli_logit_lpmf(h[trial, agent] | bias + memory[trial, agent] * beta);
}
}
}
generated quantities{
real bias_prior;
real beta_prior;
int<lower=0, upper = trials> prior_preds0;
int<lower=0, upper = trials> prior_preds1;
int<lower=0, upper = trials> prior_preds2;
int<lower=0, upper = trials> posterior_preds0;
int<lower=0, upper = trials> posterior_preds1;
int<lower=0, upper = trials> posterior_preds2;
bias_prior = normal_rng(0,1);
beta_prior = normal_rng(0,1);
prior_preds0 = binomial_rng(trials, inv_logit(bias_prior + 0 * beta_prior));
prior_preds1 = binomial_rng(trials, inv_logit(bias_prior + 1 * beta_prior));
prior_preds2 = binomial_rng(trials, inv_logit(bias_prior + 2 * beta_prior));
posterior_preds0 = binomial_rng(trials, inv_logit(bias + 0 * (beta)));
posterior_preds1 = binomial_rng(trials, inv_logit(bias + 1 * (beta)));
posterior_preds2 = binomial_rng(trials, inv_logit(bias + 2 * (beta)));
}
"
write_stan_file(
stan_model,
dir = "stan/",
basename = "W5_MultilevelMemory_fullpooling.stan")
file <- file.path("stan/W5_MultilevelMemory_fullpooling.stan")
mod <- cmdstan_model(file, cpp_options = list(stan_threads = TRUE),
stanc_options = list("O1"))
# The following command calls Stan with specific options.
samples <- mod$sample(
data = data,
seed = 123,
chains = 2,
parallel_chains = 2,
threads_per_chain = 2,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 500,
max_treedepth = 20,
adapt_delta = 0.99,
)
samples$save_object(file = "simmodels/W5_MultilevelMemory_fullpooling.RDS")[MISSING: Evaluation of FULL POOLING]
[MISSING: PARAMETER RECOVERY IN A MULTILEVEL FRAMEWORK (IND VS POP)]