Chapter 7 Model comparison
[MISSING INTRO]
Imagine having several models of what might be going on and want to know which is the best explanation of the data. E.g. Are people more likely to use a memory strategy, or a win stay lose shift strategy? Or are we justified in assuming that people react differently to losses than to wins (e.g. by being more likely to shift when losing, than to stay when winning)? Or would we be justified in assuming that capuchin monkeys and cognitive science students use the same model?
Model comparison defines a broad range of practices aimed at identifying among a set of models the best model for a given data set. What “best” means is, however, a non-trivial question. Ideally, “best” would mean the model describing the mechanism that actually generated the data. However, as we will see that is a tricky proposition and we analysts tend to rely on proxies. There are many of such proxies in the literature. For instance, Nicenboim et al (2023) suggests employing either Bayes Factors or cross-validation (https://vasishth.github.io/bayescogsci/book/ch-comparison.html). In this course, we rely on cross-validation based predictive performance (this chapter) and mixture models (next chapter).
In other words, this chapter will assess models in terms of their (estimated) ability to predict new (test) data. Remember that predictive performance is a very useful tool, but not a magical solution. It allows us to combat overfitting to the training sample (your model snuggling to your data so much that it fits both signal and noise), but it has key limitations, which we will discuss at the end of the chapter.
To learn how to make model comparison, in this chapter, we rely on our usual simulation based approach to ensure that the method is doing what we want. We simulate the behavior of biased agents playing against the memory agents. This provides us with data generated according to two different mechanisms: biased agents and memory agents. We can fit both models separately on each of the two sets of agents, so we can compare the relative performance of the two models: can we identify the true model generating the data (in a setup where truth is known)? This is what is usually called “model recovery” and complements nicely “parameter recovery”. In model recovery we assess whether we can identify the correct model, in parameter recovery we assess whether - once we know the correct model - we can identify the correct parameter values.
Let’s get going.
7.1 Define parameters
pacman::p_load(tidyverse,
here,
posterior,
cmdstanr,
brms,
tidybayes,
loo, job)
# Shared parameters
agents <- 100
trials <- 120
noise <- 0
# Biased agents parameters
rateM <- 1.386 # roughly 0.8 once inv_logit scaled
rateSD <- 0.65 # roughly giving a sd of 0.1 in prob scale
# Memory agents parameters
biasM <- 0
biasSD <- 0.1
betaM <- 1.5
betaSD <- 0.37.2 Define biased and memory agents
# Functions of the agents
RandomAgentNoise_f <- function(rate, noise) {
choice <- rbinom(1, 1, inv_logit_scaled(rate))
if (rbinom(1, 1, noise) == 1) {
choice = rbinom(1, 1, 0.5)
}
return(choice)
}
MemoryAgentNoise_f <- function(bias, beta, otherRate, noise) {
rate <- inv_logit_scaled(bias + beta * logit_scaled(otherRate))
choice <- rbinom(1, 1, rate)
if (rbinom(1, 1, noise) == 1) {
choice = rbinom(1, 1, 0.5)
}
return(choice)
}7.3 Generating the agents
[MISSING: PARALLELIZE]
# Looping through all the agents to generate the data.
d <- NULL
for (agent in 1:agents) {
rate <- rnorm(1, rateM, rateSD)
bias <- rnorm(1, biasM, biasSD)
beta <- rnorm(1, betaM, betaSD)
randomChoice <- rep(NA, trials)
memoryChoice <- rep(NA, trials)
memoryRate <- rep(NA, trials)
for (trial in 1:trials) {
randomChoice[trial] <- RandomAgentNoise_f(rate, noise)
if (trial == 1) {
memoryChoice[trial] <- rbinom(1,1,0.5)
} else {
memoryChoice[trial] <- MemoryAgentNoise_f(bias, beta, mean(randomChoice[1:trial], na.rm = T), noise)
}
}
temp <- tibble(agent, trial = seq(trials), randomChoice, randomRate = rate, memoryChoice, memoryRate, noise, rateM, rateSD, bias, beta, biasM, biasSD, betaM, betaSD)
if (agent > 1) {
d <- rbind(d, temp)
} else{
d <- temp
}
}
d <- d %>% group_by(agent) %>% mutate(
randomRate = cumsum(randomChoice) / seq_along(randomChoice),
memoryRate = cumsum(memoryChoice) / seq_along(memoryChoice)
)7.4 Prep the data
d1 <- d %>%
subset(select = c(agent, randomChoice)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = randomChoice)
d2 <- d %>%
subset(select = c(agent, memoryChoice)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = memoryChoice)
## Create the data
data_biased <- list(
trials = trials,
agents = agents,
h = as.matrix(d1[,2:101]),
other = as.matrix(d2[,2:101])
)
data_memory <- list(
trials = trials,
agents = agents,
h = as.matrix(d2[,2:101]),
other = as.matrix(d1[,2:101])
)7.5 Log posterior likelihood
While the previous sections did not present any new materials (and therefore weren’t much commented), as we create our Stan models to fit to the data, we need to (re)introduce the notion of log-likelihood, or even better, log posterior likelihood.
Given certain values for our parameters (let’s say a bias of 0 and beta for memory of 1) and for our variables (let’s say the vector of memory values estimated by the agent on a trial by trial basis), the model will predict a certain distribution of outcomes, that is, a certain distribution of choices (n times right, m times left hand). Comparing this to the actual data, we can identify how likely the model is to produce it. In other words, the probability that the model will actually generate the data we observed out of all its possible outcomes. Remember that we are doing Bayesian statistics, so this probability needs to be combined with the probability of the parameter values given the priors on those parameters. This would give us a posterior likelihood of the model’s parameter values given the data. The last step is that we need to work on a log scale. Working on a log scale is very useful because it avoids low probabilities (close to 0) being rounded down to exactly 0. [MISSING A LINK TO A LENGTHIER EXPLANATION]. By log-transforming the posterior likelihood, we now have the log-posterior likelihood.
Now, remember that our agent’s memory varies on a trial by trial level. In other words, for each data point, for each agent we can calculate separate values of log-posterior likelihood for each of the possible values of the parameters. That is, we can have a distribution of log-posterior likelihood for each data point.
Luckily for us telling Stan to calculate and such distributions is extremely easy: we just need to add to the generated quantities block the same log probability density/mass statement that we use in the model block, but here we specify it should be saved (replacing target += with an actual variable to be filled).
N.B. Some of you might be wandering: if Stan is already using the log-posterior probability in the sampling process, why do we need to tell it to calculate and save it? Fair enough point. But Stan does not save by default (to avoid clogging your computer with endless data) and we need the log posterior likelihood saved as “log_lik” in order to be able to use more automated functions later on.
7.6 Create the models: multilevel biased agents
Remember to add the log_lik part in the generated quantities block!
stan_biased_model <- "
functions{
real normal_lb_rng(real mu, real sigma, real lb) { // normal distribution with a lower bound
real p = normal_cdf(lb | mu, sigma); // cdf for bounds
real u = uniform_rng(p, 1);
return (sigma * inv_Phi(u)) + mu; // inverse cdf for value
}
}
// The input (data) for the model. n of trials and h of hands
data {
int<lower = 1> trials;
int<lower = 1> agents;
array[trials, agents] int h;
}
// The parameters accepted by the model.
parameters {
real thetaM;
real<lower = 0> thetaSD;
array[agents] real theta;
}
// The model to be estimated.
model {
target += normal_lpdf(thetaM | 0, 1);
target += normal_lpdf(thetaSD | 0, .3) -
normal_lccdf(0 | 0, .3);
// The prior for theta is a uniform distribution between 0 and 1
target += normal_lpdf(theta | thetaM, thetaSD);
for (i in 1:agents)
target += bernoulli_logit_lpmf(h[,i] | theta[i]);
}
generated quantities{
real thetaM_prior;
real<lower=0> thetaSD_prior;
real<lower=0, upper=1> theta_prior;
real<lower=0, upper=1> theta_posterior;
int<lower=0, upper = trials> prior_preds;
int<lower=0, upper = trials> posterior_preds;
array[trials, agents] real log_lik;
thetaM_prior = normal_rng(0,1);
thetaSD_prior = normal_lb_rng(0,0.3,0);
theta_prior = inv_logit(normal_rng(thetaM_prior, thetaSD_prior));
theta_posterior = inv_logit(normal_rng(thetaM, thetaSD));
prior_preds = binomial_rng(trials, inv_logit(thetaM_prior));
posterior_preds = binomial_rng(trials, inv_logit(thetaM));
for (i in 1:agents){
for (t in 1:trials){
log_lik[t,i] = bernoulli_logit_lpmf(h[t,i] | theta[i]);
}
}
}
"
write_stan_file(
stan_biased_model,
dir = "stan/",
basename = "W6_MultilevelBias.stan")
file <- file.path("stan/W6_MultilevelBias.stan")
mod_biased <- cmdstan_model(file,
cpp_options = list(stan_threads = TRUE),
stanc_options = list("O1"))7.7 Multilevel memory model
stan_memory_model <- "
functions{
real normal_lb_rng(real mu, real sigma, real lb) {
real p = normal_cdf(lb | mu, sigma); // cdf for bounds
real u = uniform_rng(p, 1);
return (sigma * inv_Phi(u)) + mu; // inverse cdf for value
}
}
// The input (data) for the model.
data {
int<lower = 1> trials;
int<lower = 1> agents;
array[trials, agents] int h;
array[trials, agents] int other;
}
// The parameters accepted by the model.
parameters {
real biasM;
real betaM;
vector<lower = 0>[2] tau;
matrix[2, agents] z_IDs;
cholesky_factor_corr[2] L_u;
}
transformed parameters {
array[trials, agents] real memory;
matrix[agents,2] IDs;
IDs = (diag_pre_multiply(tau, L_u) * z_IDs)';
for (agent in 1:agents){
for (trial in 1:trials){
if (trial == 1) {
memory[trial, agent] = 0.5;
}
if (trial < trials){
memory[trial + 1, agent] = memory[trial, agent] + ((other[trial, agent] - memory[trial, agent]) / trial);
if (memory[trial + 1, agent] == 0){memory[trial + 1, agent] = 0.01;}
if (memory[trial + 1, agent] == 1){memory[trial + 1, agent] = 0.99;}
}
}
}
}
// The model to be estimated.
model {
target += normal_lpdf(biasM | 0, 1);
target += normal_lpdf(tau[1] | 0, .3) -
normal_lccdf(0 | 0, .3);
target += normal_lpdf(betaM | 0, .3);
target += normal_lpdf(tau[2] | 0, .3) -
normal_lccdf(0 | 0, .3);
target += lkj_corr_cholesky_lpdf(L_u | 2);
target += std_normal_lpdf(to_vector(z_IDs));
for (agent in 1:agents){
for (trial in 1:trials){
target += bernoulli_logit_lpmf(h[trial, agent] | biasM + IDs[agent, 1] + memory[trial, agent] * (betaM + IDs[agent, 2]));
}
}
}
generated quantities{
real biasM_prior;
real<lower=0> biasSD_prior;
real betaM_prior;
real<lower=0> betaSD_prior;
real bias_prior;
real beta_prior;
array[agents] int<lower=0, upper = trials> prior_preds0;
array[agents] int<lower=0, upper = trials> prior_preds1;
array[agents] int<lower=0, upper = trials> prior_preds2;
array[agents] int<lower=0, upper = trials> posterior_preds0;
array[agents] int<lower=0, upper = trials> posterior_preds1;
array[agents] int<lower=0, upper = trials> posterior_preds2;
array[trials, agents] real log_lik;
biasM_prior = normal_rng(0,1);
biasSD_prior = normal_lb_rng(0,0.3,0);
betaM_prior = normal_rng(0,1);
betaSD_prior = normal_lb_rng(0,0.3,0);
bias_prior = normal_rng(biasM_prior, biasSD_prior);
beta_prior = normal_rng(betaM_prior, betaSD_prior);
for (i in 1:agents){
prior_preds0[i] = binomial_rng(trials, inv_logit(bias_prior + 0 * beta_prior));
prior_preds1[i] = binomial_rng(trials, inv_logit(bias_prior + 1 * beta_prior));
prior_preds2[i] = binomial_rng(trials, inv_logit(bias_prior + 2 * beta_prior));
posterior_preds0[i] = binomial_rng(trials, inv_logit(biasM + IDs[i,1] + 0 * (betaM + IDs[i,2])));
posterior_preds1[i] = binomial_rng(trials, inv_logit(biasM + IDs[i,1] + 1 * (betaM + IDs[i,2])));
posterior_preds2[i] = binomial_rng(trials, inv_logit(biasM + IDs[i,1] + 2 * (betaM + IDs[i,2])));
for (t in 1:trials){
log_lik[t,i] = bernoulli_logit_lpmf(h[t, i] | biasM + IDs[i, 1] + memory[t, i] * (betaM + IDs[i, 2]));
}
}
}
"
write_stan_file(
stan_memory_model,
dir = "stan/",
basename = "W6_MultilevelMemory.stan")
file <- file.path("stan/W6_MultilevelMemory.stan")
mod_memory <- cmdstan_model(file, cpp_options = list(stan_threads = TRUE),
stanc_options = list("O1"))7.8 Fitting the models to the data
# Fitting biased agent model to biased agent data
fit_biased2biased <- mod_biased$sample(
data = data_biased,
seed = 123,
chains = 1,
parallel_chains = 1,
threads_per_chain = 4,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 0,
output_dir = "simmodels",
max_treedepth = 20,
adapt_delta = 0.99
)
fit_biased2biased$save_object(file = "simmodels/W6_fit_biased2biased.RDS")
# Fitting biased agent model to memory agent data
fit_biased2memory <- mod_biased$sample(
data = data_memory,
seed = 123,
chains = 1,
parallel_chains = 1,
threads_per_chain = 4,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 0,
output_dir = "simmodels",
max_treedepth = 20,
adapt_delta = 0.99
)
fit_biased2memory$save_object(file = "simmodels/W6_fit_biased2memory.RDS")
fit_memory2biased <- mod_memory$sample(
data = data_biased,
seed = 123,
chains = 1,
parallel_chains = 1,
threads_per_chain = 4,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 0,
output_dir = "simmodels",
max_treedepth = 20,
adapt_delta = 0.99
)
fit_memory2biased$save_object(file = "simmodels/W6_fit_memory2biased.RDS")
fit_memory2memory <- mod_memory$sample(
data = data_memory,
seed = 123,
chains = 1,
parallel_chains = 1,
threads_per_chain = 4,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 0,
output_dir = "simmodels",
max_treedepth = 20,
adapt_delta = 0.99
)
fit_memory2memory$save_object(file = "simmodels/W6_fit_memory2memory.RDS")7.9 Calculating the expected log predictive density of a model
In the previous section, we fitted each model (biased and memory) to each dataset (biased and memory), and calculated and saved the log-posterior likelihood distributions for each data point. However, as we know from previous courses, calculating the goodness of fit of a model on the actual data it has been trained/fitted on is a bad idea. Models - expecially complex models - tend to overfit to the data. The multilevel implementation we have used is a bit skeptical of the data (it pools information across agents and combines it with the data from any given agent, thus de facto regularizing the estimates). Still overfitting is a serious risk.
Machine learning has made common practices of validation, that is, of keeping parts of the dataset out of the training/fitting process, in order to then see how well the trained model can predict those untouched data, and get an out of sample error. [RANT ON INTERNAL VS. EXTERNAL TEST SET: HOW WELL DOES IT GENERALIZE TO DIVERSE CONTEXTS?].
When the datasets are small, as it is often the case in cognitive science, keeping a substantial portion of the data out - substantial enough to be representative of a more general population - is problematic as it risks starving the model of data: there might not be enough data for reliable estimation of the parameter values. This is where the notion of cross-validation comes in: we can split the dataset in k folds, let’s say k = 10. Then each fold is in turn kept aside as validation set, the model is fitted on the other folds, and its predictive performance tested on the validation set. Repeat this operation of each of the folds. This operation ensures that all the data can be used for training as well as for validation, and is in its own terms quite genial. However, this does not mean it is free of shortcomings. First, small validation folds might not be representative of the diversity of true out-of-sample populations - and there is a tendency to set k equal to the number of datapoints (leave-one-out cross validation). Second, there are many ways in which information could leak or contaminate across folds if the pipeline is not very careful (e.g. via data preprocessing scaling the full dataset, or hyper-parameter estimation). Third, and crucial for our case here, cross validation implies refitting the model k times, which for Bayesian models might be very cumbersome (I once had a model that took 6 weeks to run).
The elpd (expected log predictive density) is an attempt at estimating the out-of-sample error without actually re-running the model. To understand elpd we need to decompose it in several steps.
Log pointwise predictive density (lppd) is the sum of the logarithm of the average log posterior likelihood of each observation ( Pr(yi) )
A penalty is given according to the sum of the variance in log posterior likelihood per each observation. The more unstable (varying) the higher the penalty.
This is all still fully based on the training sample. Elpd moves it one step forward by weighting the lppd according to the frequency of the observation in the dataset excluding that observation. The more frequent, the more it matters. N.B. elpd only keeps one datapoint out, meaning that dependencies within larger clusters (e.g. repeated measures by participants) confound the measure.
Let’s calculate this, and then we will implement a more properly cross-validated version.
fit_biased2biased <- readRDS("simmodels/W6_fit_memory2memory.RDS")
Loo_biased2biased <- fit_biased2biased$loo(save_psis = TRUE, cores = 4)
p1 <- plot(Loo_biased2biased)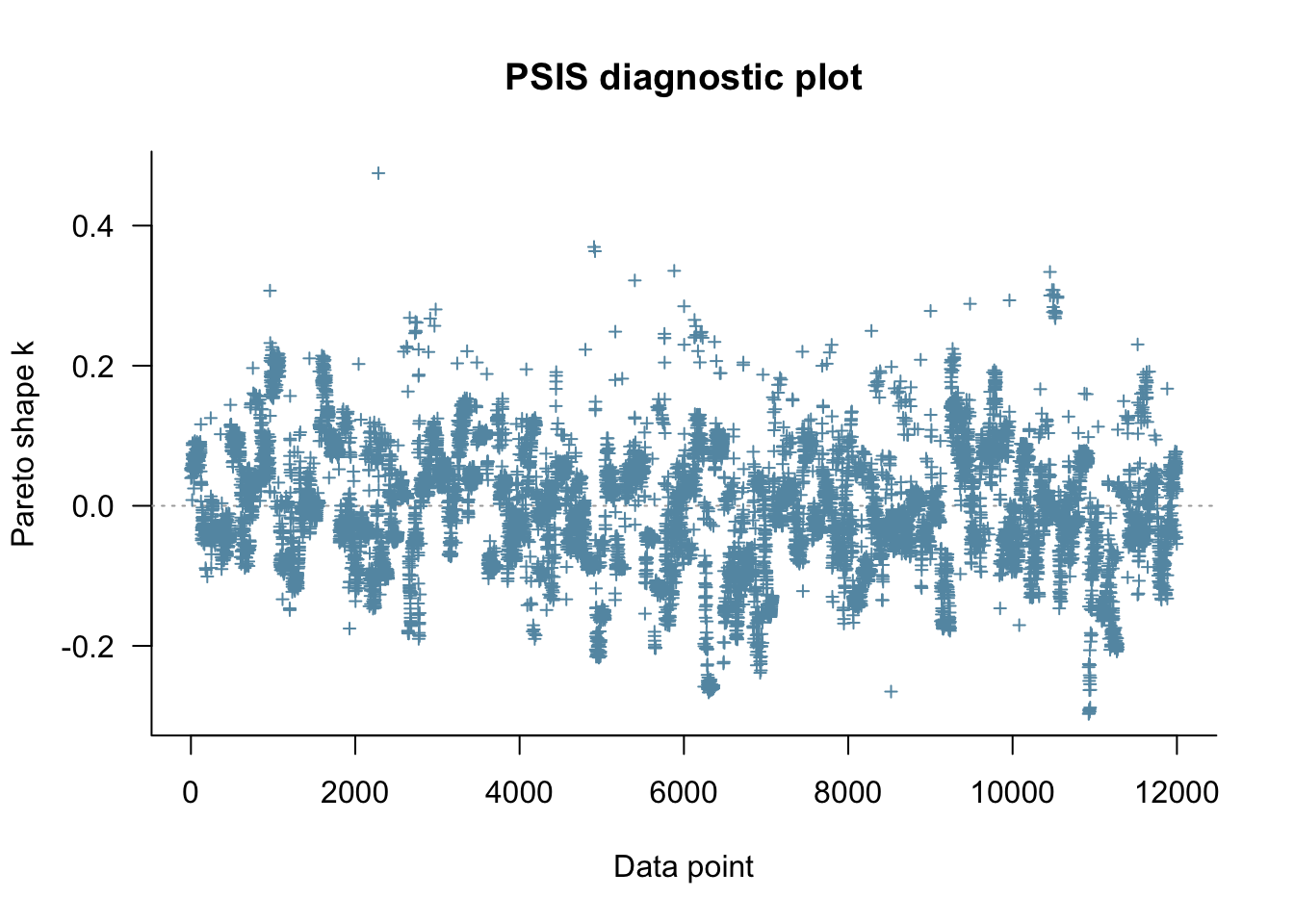
p1 <- p1 + ylim(-0.4, 0.4)
fit_biased2memory <- readRDS("simmodels/W6_fit_biased2memory.RDS")
Loo_biased2memory <- fit_biased2memory$loo(save_psis = TRUE, cores = 4)
plot(Loo_biased2memory)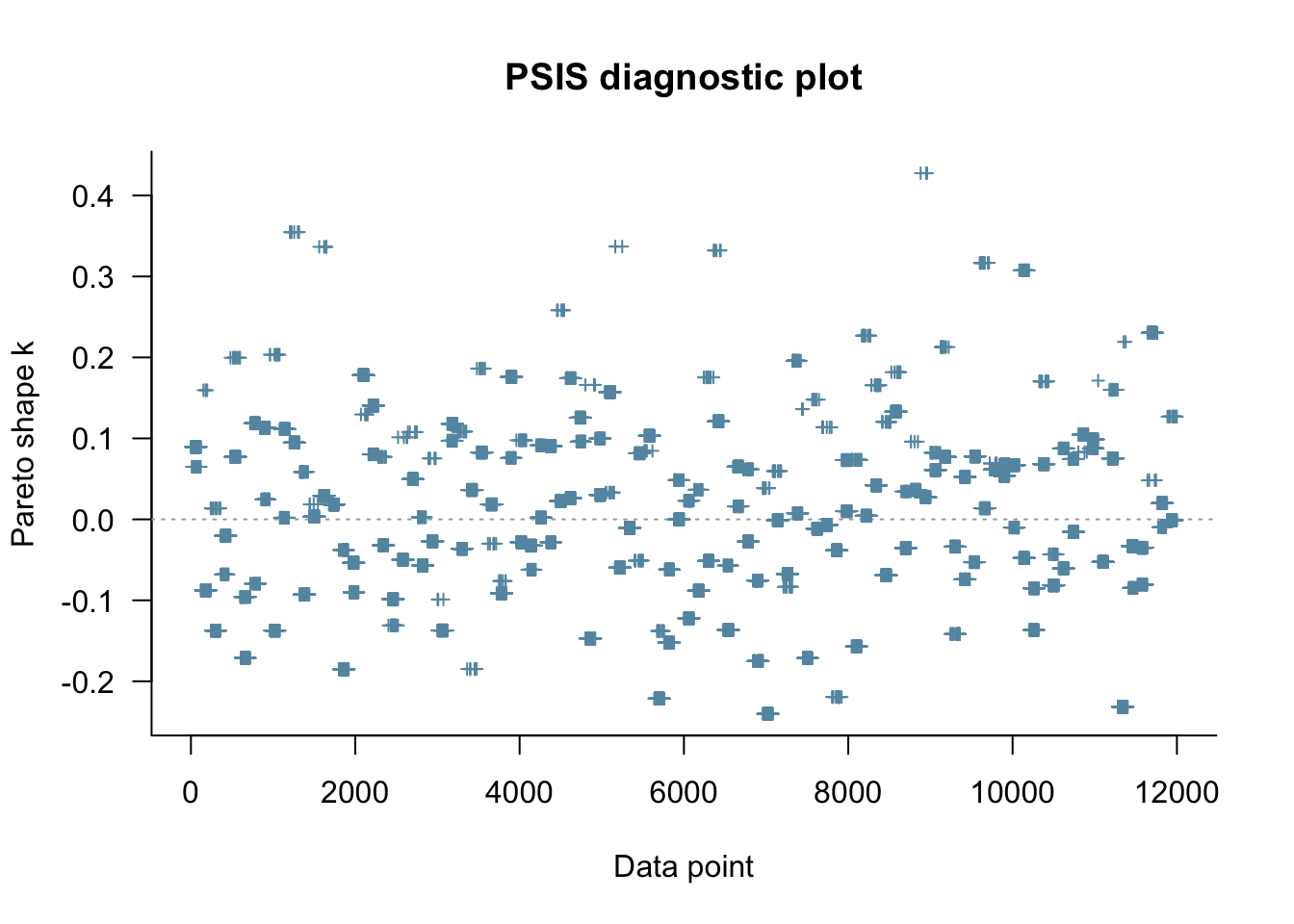
fit_memory2biased <- readRDS("simmodels/W6_fit_memory2biased.RDS")
Loo_memory2biased <- fit_memory2biased$loo(save_psis = TRUE, cores = 4)
plot(Loo_memory2biased)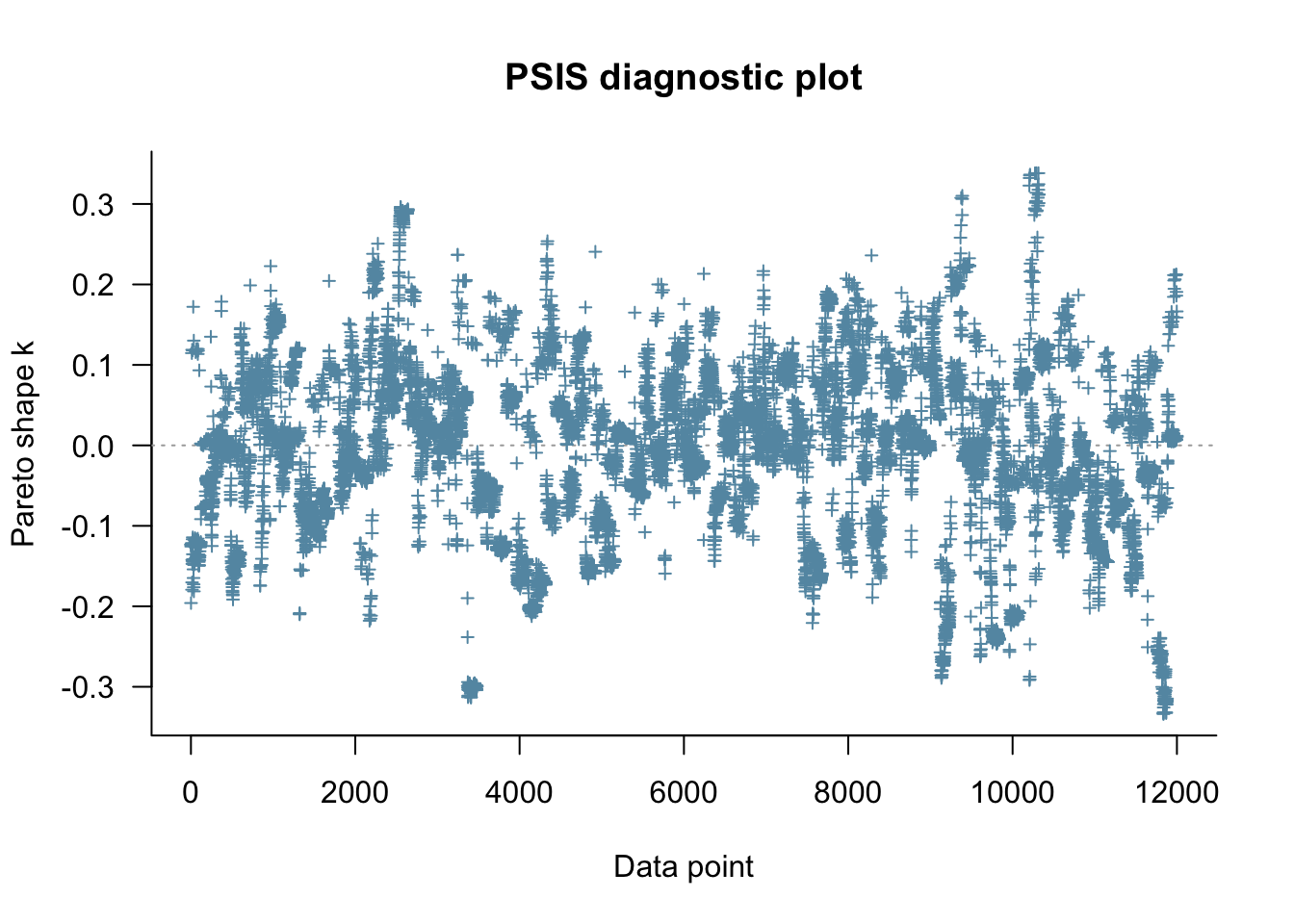
fit_memory2memory <- readRDS("simmodels/W6_fit_memory2memory.RDS")
Loo_memory2memory <- fit_memory2memory$loo(save_psis = TRUE, cores = 4)
plot(Loo_memory2memory)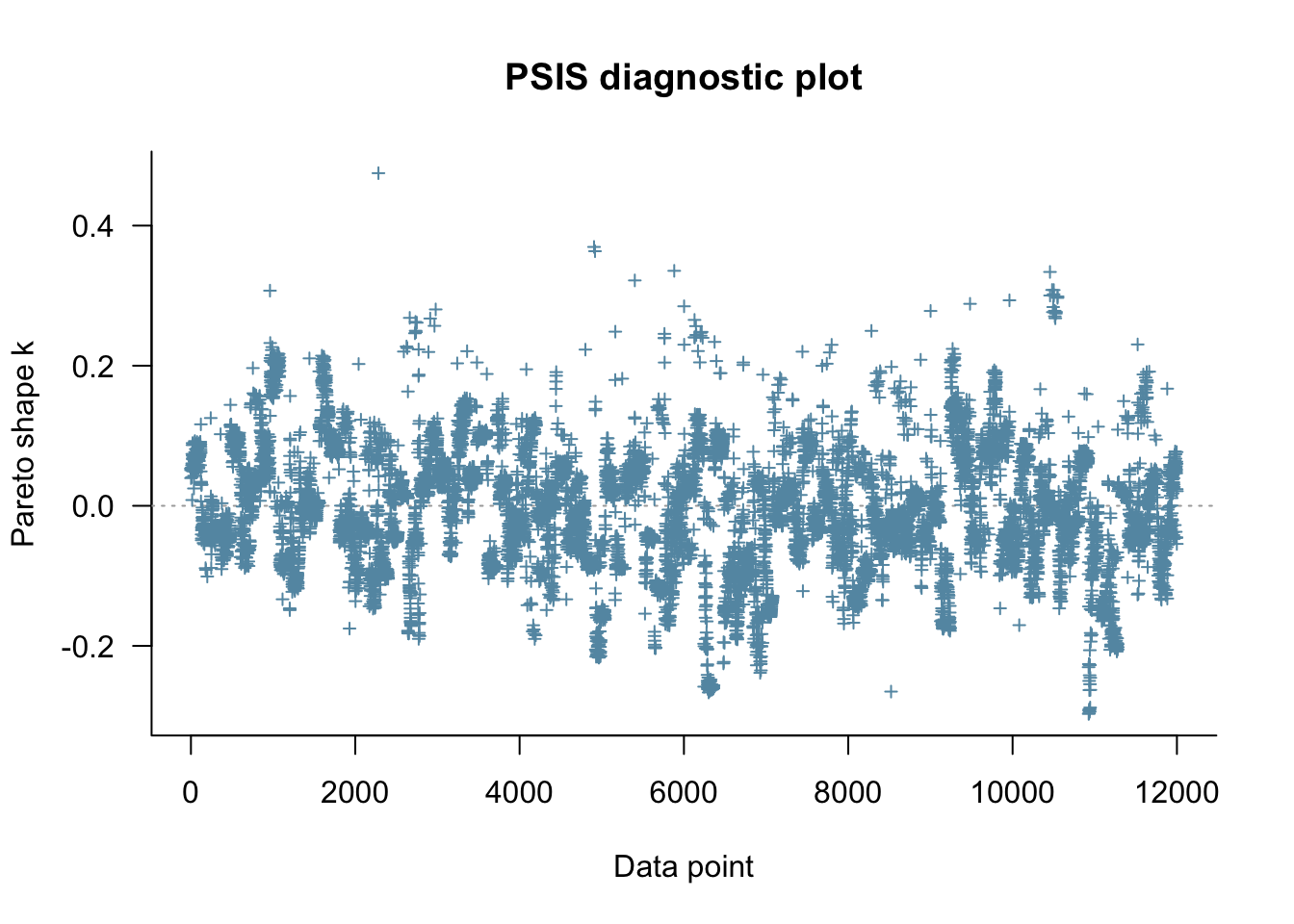
elpd <- tibble(
n = seq(12000),
biased_diff_elpd =
Loo_biased2biased$pointwise[, "elpd_loo"] -
Loo_memory2biased$pointwise[, "elpd_loo"],
memory_diff_elpd =
Loo_memory2memory$pointwise[, "elpd_loo"] -
Loo_biased2memory$pointwise[, "elpd_loo"])
p1 <- ggplot(elpd, aes(x = n, y = biased_diff_elpd)) +
geom_point(alpha = .1) +
#xlim(.5,1.01) +
#ylim(-1.5,1.5) +
geom_hline(yintercept = 0, color = "red", linetype = "dashed") +
theme_bw()
p2 <- ggplot(elpd, aes(x = n, y = memory_diff_elpd)) +
geom_point(alpha = .1) +
#xlim(.5,1.01) +
#ylim(-1.5,1.5) +
geom_hline(yintercept = 0, color = "red", linetype = "dashed") +
theme_bw()
library(patchwork)
p1 + p2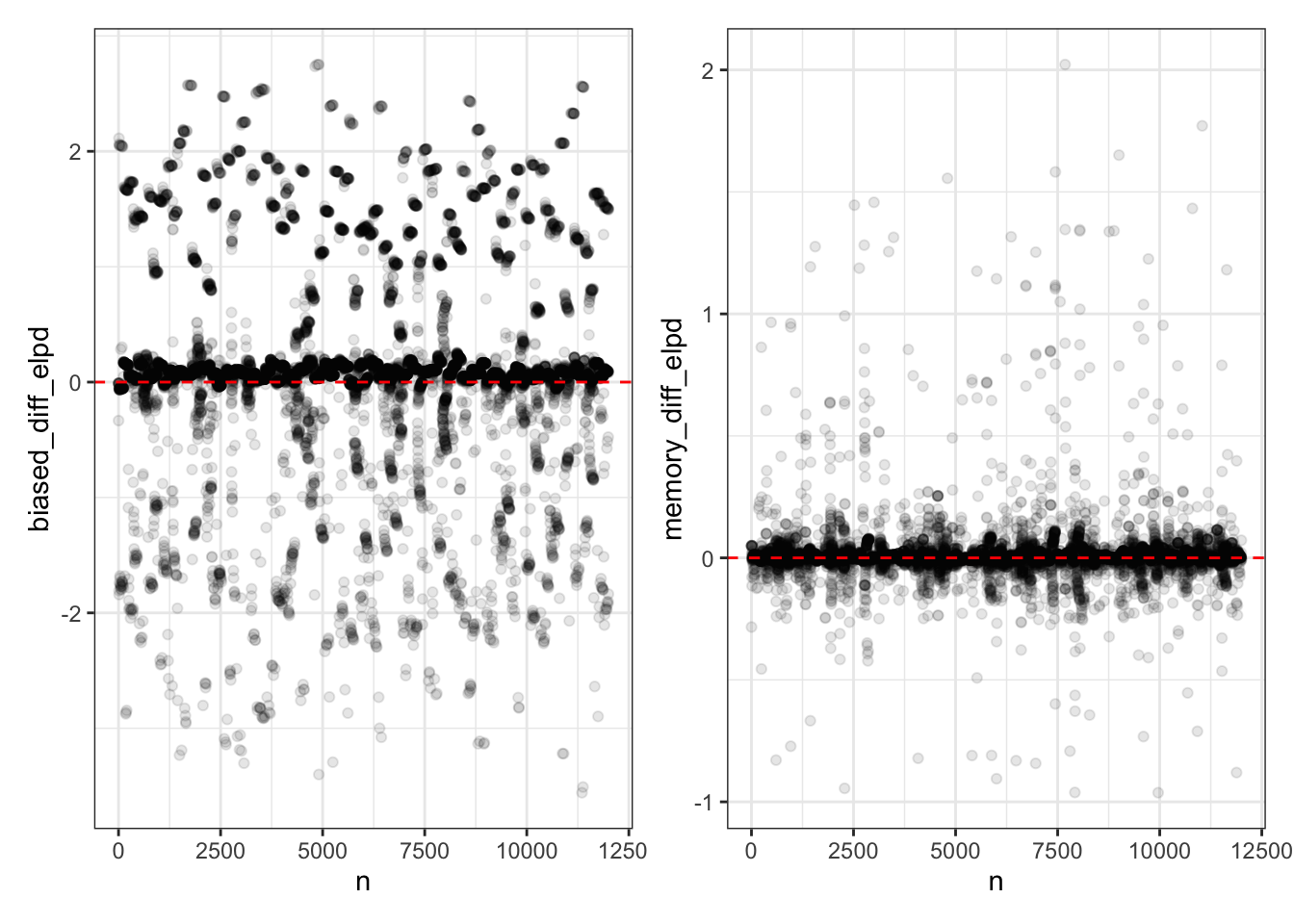
## elpd_diff se_diff
## model1 0.0 0.0
## model2 -1414.1 83.1## elpd_diff se_diff
## model2 0.0 0.0
## model1 -127.1 11.9## Method: stacking
## ------
## weight
## model1 0.768
## model2 0.232## Method: stacking
## ------
## weight
## model1 0.000
## model2 1.0007.10 Implementing Cross-Validation
As we mentioned, elpd per se is only an approximation of the cross-validated performance and it only leaves one datapoint out at a time. [MISSING: VERSION W TRANSFORMED DATA]
7.10.1 Create cross-validation ready stan model for biased agents
N.B. compared to before we also need to include specifics for test data
stan_biased_cv_model <- "
//
// This STAN model infers a random bias from a sequences of 1s and 0s (right and left). Now multilevel
//
functions{
real normal_lb_rng(real mu, real sigma, real lb) { // normal distribution with a lower bound
real p = normal_cdf(lb | mu, sigma); // cdf for bounds
real u = uniform_rng(p, 1);
return (sigma * inv_Phi(u)) + mu; // inverse cdf for value
}
}
// The input (data) for the model. n of trials and h of hands
data {
int<lower = 1> trials;
int<lower = 1> agents;
array[trials, agents] int h;
int<lower = 1> agents_test;
array[trials, agents_test] int h_test;
}
// The parameters accepted by the model.
parameters {
real thetaM;
real<lower = 0> thetaSD;
array[agents] real theta;
}
// The model to be estimated.
model {
target += normal_lpdf(thetaM | 0, 1);
target += normal_lpdf(thetaSD | 0, .3) -
normal_lccdf(0 | 0, .3);
// The prior for theta is a uniform distribution between 0 and 1
target += normal_lpdf(theta | thetaM, thetaSD);
for (i in 1:agents)
target += bernoulli_logit_lpmf(h[,i] | theta[i]);
}
generated quantities{
real thetaM_prior;
real<lower=0> thetaSD_prior;
real<lower=0, upper=1> theta_prior;
real<lower=0, upper=1> theta_posterior;
int<lower=0, upper = trials> prior_preds;
int<lower=0, upper = trials> posterior_preds;
array[trials, agents] real log_lik;
array[trials, agents_test] real log_lik_test;
thetaM_prior = normal_rng(0,1);
thetaSD_prior = normal_lb_rng(0,0.3,0);
theta_prior = inv_logit(normal_rng(thetaM_prior, thetaSD_prior));
theta_posterior = inv_logit(normal_rng(thetaM, thetaSD));
prior_preds = binomial_rng(trials, inv_logit(thetaM_prior));
posterior_preds = binomial_rng(trials, inv_logit(thetaM));
for (i in 1:agents){
for (t in 1:trials){
log_lik[t,i] = bernoulli_logit_lpmf(h[t,i] | theta[i]);
}
}
for (i in 1:agents_test){
for (t in 1:trials){
log_lik_test[t,i] = bernoulli_lpmf(h_test[t,i] | theta_posterior);
}
}
}
"
write_stan_file(
stan_biased_cv_model,
dir = "stan/",
basename = "W6_MultilevelBias_cv.stan")## [1] "/Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/stan/W6_MultilevelBias_cv.stan"7.10.2 Create cross-validation ready stan model for memory agents
stan_memory_cv_model <- "
//
// This STAN model infers a random bias from a sequences of 1s and 0s (heads and tails)
//
functions{
real normal_lb_rng(real mu, real sigma, real lb) {
real p = normal_cdf(lb | mu, sigma); // cdf for bounds
real u = uniform_rng(p, 1);
return (sigma * inv_Phi(u)) + mu; // inverse cdf for value
}
}
// The input (data) for the model.
data {
int<lower = 1> trials;
int<lower = 1> agents;
array[trials, agents] int h;
array[trials, agents] int other;
int<lower = 1> agents_test;
array[trials, agents_test] int h_test;
array[trials, agents_test] int other_test;
}
// The parameters accepted by the model.
parameters {
real biasM;
real betaM;
vector<lower = 0>[2] tau;
matrix[2, agents] z_IDs;
cholesky_factor_corr[2] L_u;
}
transformed parameters {
array[trials, agents] real memory;
array[trials, agents_test] real memory_test;
matrix[agents,2] IDs;
IDs = (diag_pre_multiply(tau, L_u) * z_IDs)';
for (agent in 1:agents){
for (trial in 1:trials){
if (trial == 1) {
memory[trial, agent] = 0.5;
}
if (trial < trials){
memory[trial + 1, agent] = memory[trial, agent] + ((other[trial, agent] - memory[trial, agent]) / trial);
if (memory[trial + 1, agent] == 0){memory[trial + 1, agent] = 0.01;}
if (memory[trial + 1, agent] == 1){memory[trial + 1, agent] = 0.99;}
}
}
}
for (agent in 1:agents_test){
for (trial in 1:trials){
if (trial == 1) {
memory_test[trial, agent] = 0.5;
}
if (trial < trials){
memory_test[trial + 1, agent] = memory_test[trial, agent] + ((other[trial, agent] - memory[trial, agent]) / trial);
if (memory_test[trial + 1, agent] == 0){memory_test[trial + 1, agent] = 0.01;}
if (memory_test[trial + 1, agent] == 1){memory_test[trial + 1, agent] = 0.99;}
}
}
}
}
// The model to be estimated.
model {
target += normal_lpdf(biasM | 0, 1);
target += normal_lpdf(tau[1] | 0, .3) -
normal_lccdf(0 | 0, .3);
target += normal_lpdf(betaM | 0, .3);
target += normal_lpdf(tau[2] | 0, .3) -
normal_lccdf(0 | 0, .3);
target += lkj_corr_cholesky_lpdf(L_u | 2);
target += std_normal_lpdf(to_vector(z_IDs));
for (agent in 1:agents){
for (trial in 1:trials){
target += bernoulli_logit_lpmf(h[trial, agent] | biasM + IDs[agent, 1] + memory[trial, agent] * (betaM + IDs[agent, 2]));
}
}
}
generated quantities{
real biasM_prior;
real<lower=0> biasSD_prior;
real betaM_prior;
real<lower=0> betaSD_prior;
real bias_prior;
real beta_prior;
array[agents] int<lower=0, upper = trials> prior_preds0;
array[agents] int<lower=0, upper = trials> prior_preds1;
array[agents] int<lower=0, upper = trials> prior_preds2;
array[agents] int<lower=0, upper = trials> posterior_preds0;
array[agents] int<lower=0, upper = trials> posterior_preds1;
array[agents] int<lower=0, upper = trials> posterior_preds2;
array[trials, agents] real log_lik;
array[trials, agents_test] real log_lik_test;
biasM_prior = normal_rng(0,1);
biasSD_prior = normal_lb_rng(0,0.3,0);
betaM_prior = normal_rng(0,1);
betaSD_prior = normal_lb_rng(0,0.3,0);
bias_prior = normal_rng(biasM_prior, biasSD_prior);
beta_prior = normal_rng(betaM_prior, betaSD_prior);
for (i in 1:agents){
prior_preds0[i] = binomial_rng(trials, inv_logit(bias_prior + 0 * beta_prior));
prior_preds1[i] = binomial_rng(trials, inv_logit(bias_prior + 1 * beta_prior));
prior_preds2[i] = binomial_rng(trials, inv_logit(bias_prior + 2 * beta_prior));
posterior_preds0[i] = binomial_rng(trials, inv_logit(biasM + IDs[i,1] + 0 * (betaM + IDs[i,2])));
posterior_preds1[i] = binomial_rng(trials, inv_logit(biasM + IDs[i,1] + 1 * (betaM + IDs[i,2])));
posterior_preds2[i] = binomial_rng(trials, inv_logit(biasM + IDs[i,1] + 2 * (betaM + IDs[i,2])));
for (t in 1:trials){
log_lik[t,i] = bernoulli_logit_lpmf(h[t, i] | biasM + IDs[i, 1] + memory[t, i] * (betaM + IDs[i, 2]));
}
}
for (i in 1:agents_test){
for (t in 1:trials){
log_lik_test[t,i] = bernoulli_logit_lpmf(h_test[t,i] | biasM + memory_test[t, i] * betaM);
}
}
}
"
write_stan_file(
stan_memory_cv_model,
dir = "stan/",
basename = "W6_MultilevelMemory_cv.stan")## [1] "/Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/stan/W6_MultilevelMemory_cv.stan"file <- file.path("stan/W6_MultilevelMemory_cv.stan")
mod_memory_cv <- cmdstan_model(file, cpp_options = list(stan_threads = TRUE),
stanc_options = list("O1"))[MISSING: PARALLELIZE]
d$fold <- kfold_split_grouped(K = 10, x = d$agent)
log_pd_biased_kfold <- matrix(nrow = 1000, ncol = 12000)
log_pd_memory_kfold <- matrix(nrow = 1000, ncol = 12000)
for (k in unique(d$fold)) {
# Training set for k
d_train <- d %>% filter(fold != k)
## Create the data
d_memory1_train <- d_train %>%
subset(select = c(agent, memoryChoice)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = memoryChoice)
d_memory2_train <- d_train %>%
subset(select = c(agent, randomChoice)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = randomChoice)
agents_n <- length(unique(d_train$agent))
d_test <- d %>%
filter(fold == k)
d_memory1_test <- d_test %>%
subset(select = c(agent, memoryChoice)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = memoryChoice)
d_memory2_test <- d_test %>%
subset(select = c(agent, randomChoice)) %>%
mutate(row = row_number()) %>%
pivot_wider(names_from = agent, values_from = randomChoice)
agents_test_n <- length(unique(d_test$agent))
data_memory <- list(
trials = trials,
agents = agents_n,
agents_test = agents_test_n,
h = as.matrix(d_memory1_train[,2:(agents_n + 1)]),
other = as.matrix(d_memory2_train[,2:(agents_n + 1)]),
h_test = as.matrix(d_memory1_test[,2:(agents_test_n + 1)]),
other_test = as.matrix(d_memory2_test[,2:(agents_test_n + 1)]))
# Train the models
fit_random <- mod_biased_cv$sample(
data = data_memory,
seed = 123,
chains = 1,
threads_per_chain = 4,
iter_warmup = 1000,
iter_sampling = 1000,
refresh = 1000,
max_treedepth = 20,
adapt_delta = 0.99
)
fit_memory <- mod_memory_cv$sample(
data = data_memory,
seed = 123,
chains = 1,
threads_per_chain = 4,
iter_warmup = 1000,
iter_sampling = 1000,
refresh = 1000,
max_treedepth = 20,
adapt_delta = 0.99
)
# Extract log likelihood which represents
# the pointwise predictive density.
# n.b. the matrix has 1000 row, and 12000 columns.
# d$fold==k yields 12000 logical values, of which 1200 TRUEs, identifying 1200 columns
## the fit blabla yields 1000 obs (samples) and 1190 variables instead of 1200
log_pd_biased_kfold[, d$fold == k] <- fit_random$draws("log_lik_test", format = "matrix")
log_pd_memory_kfold[, d$fold == k] <- fit_memory$draws("log_lik_test", format = "matrix")
}
save(log_pd_biased_kfold, log_pd_memory_kfold, file = "simmodels/W6_CV_Biased&Memory.RData")7.11 Calculating elpd and comparing
load("simmodels/W6_CV_Biased&Memory.RData")
elpd_biased_kfold <- elpd(log_pd_biased_kfold)
elpd_memory_kfold <- elpd(log_pd_memory_kfold)
loo_compare(elpd_biased_kfold, elpd_memory_kfold)## elpd_diff se_diff
## model1 0.0 0.0
## model2 -437.3 23.97.12 Limitations of model comparison techniques
- it might be overfitting to the training population, that is, to the
7.13 Mixture models
7.13.1 Load the dataset
We load the data set from chapter NN, where we loop through possible rates and noise levels, and pick one agent to build up the model progressively.
## Rows: 7920 Columns: 5
## ── Column specification ────────────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (5): trial, choice, rate, noise, cumulativerate
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.7.14 Stan model mixing biased and noise
We then build a Stan model with the noise parameter
stan_mixture_model <- "
// This Stan model defines a mixture of bernoulli (random bias + noise)
//
// The input (data) for the model. n of trials and h of heads
data {
int<lower=1> n;
array[n] int h;
}
// The parameters accepted by the model.
parameters {
real bias;
real noise;
}
// The model to be estimated.
model {
// The prior for theta is a uniform distribution between 0 and 1
target += normal_lpdf(bias | 0, 1);
target += normal_lpdf(noise | 0, 1);
// The model consists of a binomial distributions with a rate theta
target += log_sum_exp(log(inv_logit(noise)) +
bernoulli_logit_lpmf(h | 0),
log1m(inv_logit(noise)) + bernoulli_logit_lpmf(h | bias));
}
generated quantities{
real<lower=0, upper=1> noise_p;
real<lower=0, upper=1> bias_p;
noise_p = inv_logit(noise);
bias_p = inv_logit(bias);
}
"
write_stan_file(
stan_mixture_model,
dir = "stan/",
basename = "W6_MixtureSingle.stan")## [1] "/Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/stan/W6_MixtureSingle.stan"7.15 Fitting and assessing the model
samples <- mod_mixture$sample(
data = data,
seed = 123,
chains = 2,
parallel_chains = 2,
threads_per_chain = 2,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 500,
max_treedepth = 20,
adapt_delta = 0.99,
)## Running MCMC with 2 parallel chains, with 2 thread(s) per chain...
##
## Chain 1 Iteration: 1 / 4000 [ 0%] (Warmup)
## Chain 1 Iteration: 500 / 4000 [ 12%] (Warmup)
## Chain 1 Iteration: 1000 / 4000 [ 25%] (Warmup)
## Chain 1 Iteration: 1500 / 4000 [ 37%] (Warmup)
## Chain 1 Iteration: 2000 / 4000 [ 50%] (Warmup)
## Chain 1 Iteration: 2001 / 4000 [ 50%] (Sampling)
## Chain 1 Iteration: 2500 / 4000 [ 62%] (Sampling)
## Chain 2 Iteration: 1 / 4000 [ 0%] (Warmup)
## Chain 2 Iteration: 500 / 4000 [ 12%] (Warmup)
## Chain 2 Iteration: 1000 / 4000 [ 25%] (Warmup)
## Chain 2 Iteration: 1500 / 4000 [ 37%] (Warmup)
## Chain 2 Iteration: 2000 / 4000 [ 50%] (Warmup)
## Chain 2 Iteration: 2001 / 4000 [ 50%] (Sampling)
## Chain 2 Iteration: 2500 / 4000 [ 62%] (Sampling)
## Chain 1 Iteration: 3000 / 4000 [ 75%] (Sampling)
## Chain 1 Iteration: 3500 / 4000 [ 87%] (Sampling)
## Chain 1 Iteration: 4000 / 4000 [100%] (Sampling)
## Chain 2 Iteration: 3000 / 4000 [ 75%] (Sampling)
## Chain 2 Iteration: 3500 / 4000 [ 87%] (Sampling)
## Chain 2 Iteration: 4000 / 4000 [100%] (Sampling)
## Chain 1 finished in 0.2 seconds.
## Chain 2 finished in 0.2 seconds.
##
## Both chains finished successfully.
## Mean chain execution time: 0.2 seconds.
## Total execution time: 0.3 seconds.save(samples, data,
file = "simmodels/W7_singlemixture.RData")
samples$save_object(file = "simmodels/W7_singlemixture.RDS")
samples$save_output_files(dir = "simmodels", basename = "W7_singlemixture")## Moved 2 files and set internal paths to new locations:
## - /Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/simmodels/W7_singlemixture-202402142307-1-7cd9f8.csv
## - /Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/simmodels/W7_singlemixture-202402142307-2-7cd9f8.csv[MISSING: EVALUATION]
7.16 Basic evaluation
## # A tibble: 5 × 10
## variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 lp__ -65.7 -65.4 1.03 0.713 -67.7 -64.7 1.00 1396. 1708.
## 2 bias 1.28 1.28 0.216 0.212 0.942 1.65 1.00 1990. 1860.
## 3 noise -0.400 -0.408 0.928 0.941 -1.92 1.11 1.00 2054. 2137.
## 4 noise_p 0.416 0.399 0.193 0.218 0.128 0.753 1.00 2054. 2137.
## 5 bias_p 0.781 0.782 0.0364 0.0361 0.719 0.839 1.00 1990. 1860.7.17 Multilevel mixture model
### Multilevel mixture
stan_multilevelMixture_model <- "
//
// This Stan model defines a mixture of bernoulli (random bias + noise)
//
functions{
real normal_lb_rng(real mu, real sigma, real lb) {
real p = normal_cdf(lb | mu, sigma); // cdf for bounds
real u = uniform_rng(p, 1);
return (sigma * inv_Phi(u)) + mu; // inverse cdf for value
}
}
// The input (data) for the model. n of trials and h of heads
data {
int<lower = 1> trials;
int<lower = 1> agents;
array[trials, agents] int h;
}
// The parameters accepted by the model.
parameters {
real thetaM;
real noiseM; // p of noise
vector<lower = 0>[2] tau;
matrix[2, agents] z_IDs;
cholesky_factor_corr[2] L_u;
}
transformed parameters {
matrix[agents,2] IDs;
IDs = (diag_pre_multiply(tau, L_u) * z_IDs)';
}
// The model to be estimated.
model {
target += normal_lpdf(thetaM | 0, 1);
target += normal_lpdf(tau[1] | 0, .3) -
normal_lccdf(0 | 0, .3);
target += normal_lpdf(noiseM | -1, .5);
target += normal_lpdf(tau[2] | 0, .3) -
normal_lccdf(0 | 0, .3);
target += lkj_corr_cholesky_lpdf(L_u | 2);
target += std_normal_lpdf(to_vector(z_IDs));
for (i in 1:agents)
target += log_sum_exp(
log(inv_logit(noiseM + IDs[i,2])) + // p of noise
bernoulli_logit_lpmf(h[,i] | 0), // times post likelihood of the noise model
log1m(inv_logit(noiseM + IDs[i,2])) + // 1 - p of noise
bernoulli_logit_lpmf(h[,i] | thetaM + IDs[i,1])); // times post likelihood of the bias model
}
generated quantities{
real thetaM_prior;
real<lower=0> thetaSD_prior;
real noiseM_prior;
real<lower=0> noiseSD_prior;
real<lower=0, upper=1> theta_prior;
real<lower=0, upper=1> noise_prior;
real<lower=0, upper=1> theta_posterior;
real<lower=0, upper=1> noise_posterior;
array[trials,agents] int<lower=0, upper = trials> prior_noise;
array[trials,agents] int<lower=0, upper = trials> posterior_noise;
array[trials,agents] int<lower=0, upper = trials> prior_preds;
array[trials,agents] int<lower=0, upper = trials> posterior_preds;
array[trials, agents] real log_lik;
thetaM_prior = normal_rng(0,1);
thetaSD_prior = normal_lb_rng(0,0.3,0);
theta_prior = inv_logit(normal_rng(thetaM_prior, thetaSD_prior));
noiseM_prior = normal_rng(-1,.5);
noiseSD_prior = normal_lb_rng(0,0.3,0);
noise_prior = inv_logit(normal_rng(noiseM_prior, noiseSD_prior));
theta_posterior = inv_logit(normal_rng(thetaM, tau[1]));
noise_posterior = inv_logit(normal_rng(noiseM, tau[2]));
for (i in 1:agents){
for (t in 1:trials){
prior_noise[t,i] = bernoulli_rng(noise_prior);
posterior_noise[t,i] = bernoulli_rng(inv_logit(noiseM + IDs[i,2]));
if(prior_noise[t,i]==1){
prior_preds[t,i] = bernoulli_rng(theta_prior);
} else{
prior_preds[t,i] = bernoulli_rng(0.5);
}
if(posterior_noise[t,i]==1){
posterior_preds[t,i] = bernoulli_rng(inv_logit(thetaM + IDs[i,1]));
} else{
posterior_preds[t,i] = bernoulli_rng(0.5);
}
log_lik[t,i] = log_sum_exp(
log(inv_logit(noiseM + IDs[i,2])) + // p of noise
bernoulli_logit_lpmf(h[t,i] | 0), // times post likelihood of the noise model
log1m(inv_logit(noiseM + IDs[i,2])) + // 1 - p of noise
bernoulli_logit_lpmf(h[t,i] | thetaM + IDs[i,1])); // times post likelihood of the bias model
}
}
}
"
write_stan_file(
stan_multilevelMixture_model,
dir = "stan/",
basename = "W6_MixtureMultilevel.stan")## [1] "/Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/stan/W6_MixtureMultilevel.stan"file <- file.path("stan/W6_MixtureMultilevel.stan")
mod_mixture <- cmdstan_model(file, cpp_options = list(stan_threads = TRUE),
stanc_options = list("O1"))
samples <- mod_mixture$sample(
data = data_biased,
seed = 123,
chains = 2,
parallel_chains = 2,
threads_per_chain = 2,
iter_warmup = 2000,
iter_sampling = 2000,
refresh = 500,
max_treedepth = 20,
adapt_delta = 0.99,
)## Running MCMC with 2 parallel chains, with 2 thread(s) per chain...
##
## Chain 1 Iteration: 1 / 4000 [ 0%] (Warmup)
## Chain 2 Iteration: 1 / 4000 [ 0%] (Warmup)
## Chain 1 Iteration: 500 / 4000 [ 12%] (Warmup)
## Chain 2 Iteration: 500 / 4000 [ 12%] (Warmup)
## Chain 1 Iteration: 1000 / 4000 [ 25%] (Warmup)
## Chain 2 Iteration: 1000 / 4000 [ 25%] (Warmup)
## Chain 1 Iteration: 1500 / 4000 [ 37%] (Warmup)
## Chain 2 Iteration: 1500 / 4000 [ 37%] (Warmup)
## Chain 1 Iteration: 2000 / 4000 [ 50%] (Warmup)
## Chain 1 Iteration: 2001 / 4000 [ 50%] (Sampling)
## Chain 2 Iteration: 2000 / 4000 [ 50%] (Warmup)
## Chain 2 Iteration: 2001 / 4000 [ 50%] (Sampling)
## Chain 1 Iteration: 2500 / 4000 [ 62%] (Sampling)
## Chain 2 Iteration: 2500 / 4000 [ 62%] (Sampling)
## Chain 1 Iteration: 3000 / 4000 [ 75%] (Sampling)
## Chain 2 Iteration: 3000 / 4000 [ 75%] (Sampling)
## Chain 1 Iteration: 3500 / 4000 [ 87%] (Sampling)
## Chain 2 Iteration: 3500 / 4000 [ 87%] (Sampling)
## Chain 1 Iteration: 4000 / 4000 [100%] (Sampling)
## Chain 1 finished in 126.5 seconds.
## Chain 2 Iteration: 4000 / 4000 [100%] (Sampling)
## Chain 2 finished in 128.0 seconds.
##
## Both chains finished successfully.
## Mean chain execution time: 127.2 seconds.
## Total execution time: 128.2 seconds.save(samples, data,
file = "simmodels/W7_multimixture.RData")
samples$save_object(file = "simmodels/W7_multimixture.RDS")
samples$save_output_files(dir = "simmodels", basename = "W7_multimixture")## Moved 2 files and set internal paths to new locations:
## - /Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/simmodels/W7_multimixture-202402142310-1-34d434.csv
## - /Users/au209589/Dropbox/Teaching/AdvancedCognitiveModeling23_book/simmodels/W7_multimixture-202402142310-2-34d434.csv[MISSING: EVALUATION]
## # A tibble: 60,417 × 10
## variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 lp__ -6.36e+3 -6.36e+3 12.4 12.3 -6.38e+3 -6.34e+3 1.00 1042. 1964.
## 2 thetaM 1.36e+0 1.36e+0 0.0681 0.0686 1.25e+0 1.48e+0 1.00 690. 1295.
## 3 noiseM -2.50e+0 -2.49e+0 0.316 0.315 -3.02e+0 -1.98e+0 1.00 4449. 2822.
## 4 tau[1] 6.13e-1 6.12e-1 0.0512 0.0501 5.32e-1 7.01e-1 1.00 1328. 2398.
## 5 tau[2] 2.04e-1 1.74e-1 0.154 0.150 1.65e-2 5.04e-1 1.00 3225. 2146.
## 6 z_IDs[1,… -9.89e-1 -9.90e-1 0.335 0.323 -1.54e+0 -4.32e-1 1.00 3404. 2731.
## 7 z_IDs[2,… -1.27e-2 -3.20e-2 0.999 0.970 -1.66e+0 1.65e+0 1.00 6980. 2385.
## 8 z_IDs[1,… 2.07e+0 2.05e+0 0.522 0.508 1.25e+0 2.97e+0 1.00 5776. 3029.
## 9 z_IDs[2,… -1.36e-2 -3.70e-3 1.00 0.980 -1.66e+0 1.64e+0 1.00 6082. 2961.
## 10 z_IDs[1,… -4.31e-1 -4.35e-1 0.356 0.362 -1.02e+0 1.60e-1 1.00 3908. 2225.
## # ℹ 60,407 more rows## Warning: Some Pareto k diagnostic values are too high. See help('pareto-k-diagnostic') for details.##
## Computed from 4000 by 12000 log-likelihood matrix
##
## Estimate SE
## elpd_loo -6171.3 52.2
## p_loo 111.5 2.5
## looic 12342.5 104.3
## ------
## Monte Carlo SE of elpd_loo is NA.
##
## Pareto k diagnostic values:
## Count Pct. Min. n_eff
## (-Inf, 0.5] (good) 11732 97.8% 586
## (0.5, 0.7] (ok) 174 1.5% 1624
## (0.7, 1] (bad) 94 0.8% 718
## (1, Inf) (very bad) 0 0.0% <NA>
## See help('pareto-k-diagnostic') for details.[MISSING: PARAMETER RECOVERY]
[MISSING: BIASED VS. MEMORY?]